D* 알고리즘

1. D* 알고리즘 이란?

• Dynamic A*

• D* 알고리즘은 시작점(Start state)에서 목표점(Goal state)까지의 경로비용을 최소화하는 서치 알고리즘 중의 하나.

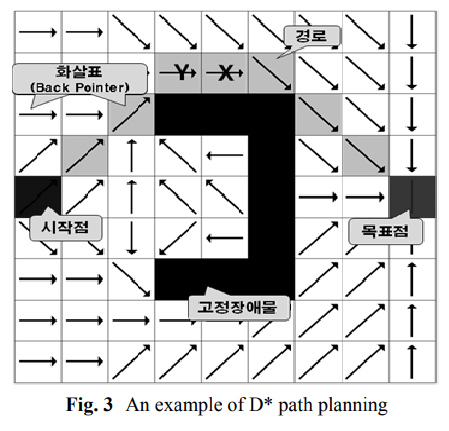
• D* 알고리즘의 전역경로계획은 지도 데이터를 바탕으로 로봇이 출발하기 전에 이루어 질 수 있는데 Fig. 3의 각 셀의 화살표(Back pointer)는 전역경로 계획된 결과를 나타낸다. 셀에서 화살표의 방향은 근처 셀 중에서 경로비용이 가장 작은 셀을 나타낸다.

• 전역 경로계획은 목표점에서 거꾸로 시작점을 찾아가는 Backward 서치 방법으로 이루어진다.

• 지역 경로 계획은 로봇의 이동 중 새로운 고정 또는 이동장애물이 발견된 경우 기존 계획된 전역경로계획 결과를 바탕으로 새로운 장애물 근방의 고유비용을 수정한 후 이를 바탕으로 주위셀들의 경로비용과 화살표(Back Pointer)를 수정하게 된다.

• D star 알고리즘은 주어진 환경의 지도데이터가 틀렸을 경우와 움직이는 장애물이 있는 경우 새로운 환경 데이터를 기반으로 다시 맵을 구성해서 새로운 환경 데이터를 기반으로 다시 맵을 구성해서 새로운 경로를 찾아야하는 A* 알고리즘과 달리 이미 계획된 전역경로계획을 기반으로 필요한 영역에서만 지역경로계획을 수행하므로 실시간으로 경로를 변경 계획하는 것이 용이하다.

2. D* 알고리즘의 비용(cost) 함수

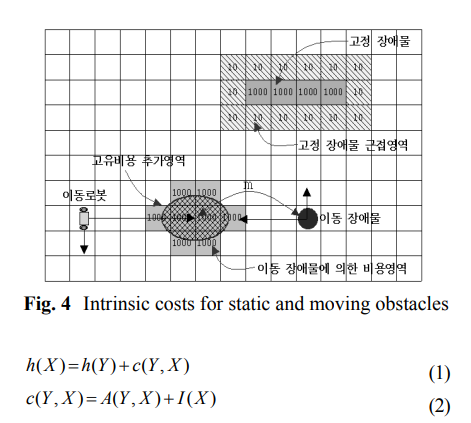
• D star 알고리즘은 경로비용을 최소화하는 알고리즘이므로 D* 알고리즘을 효율적으로 사용하기 위해서 경로 비용의 설계가 매우 중요한 역할을 한다.

• 식 (1)에서 h(X)는, 예를 들어 Fig 3에서 상태 X까지 소요되는 총 경로비용이며 Y는 상태 X에 도달하기 바로 이전 상태를 의미하며, 식 (2)에서 c(X,Y)는 근접 경로 비용으로 이전 상태 Y에서 현재 상태 X로의 경로 비용을 의미한다.

• 식 (2)에서 A(X,Y)는 상태 X와 상태 Y로 이동하는데 드는 비용이며, I(X)는 상태의 고유비용으로 인접 고정 장애물과 이동 장애물을 고려한 비용 함수이다.

3. D* 알고리즘의 장단점

• 장점

  • 전역 경로계획 뿐만 아니라 지역 경로계획도 동시에 사용 가능하다.

  • 예기치 못한 고정 장애물이나 움직이는 장애물을 회피하여 주어진 목적지까지 빠르게 도달할 수 있는 지역 경로계획을 신속히 알고리즘 통해 구현할 수 있다.

• 단점

  • 다른 알고리즘에 비해서 많은 데이터 저장공간을 필요로 한다.

출처 : https://www.koreascience.or.kr/article/JAKO201022262413085.pdf

4. D* lite 알고리즘

• LPA star 를 기반으로 하는 Sven Koenig 및 Maxim Likhachev 의 증분 휴리스틱 검색 알고리즘 , A* 및 Dynamic SWSF-FP 의 아이디어를 결합한 증분 휴리스틱 검색 알고리즘

• D star lite 는 원래 D star 또는 Focused D* 를 기반으로 하지 않지만 동일한 동작을 구현한다. 이해하기 쉽고 더 적은 수의 코드 줄로 구현할 수 있으므로 이름이 "D star Lite".

• LPA* 알고리즘

  • Lifelong Planning A*

  • A* 를 기반으로 하는 증분 휴리스틱 검색 알고리즘

  • A star 와 마찬가지로 LPA* 는 주어진 노드에서 목표까지의 경로 비용에 대한 하한선인 발견적 방법을 사용한다.

  • 휴리스틱이 음수가 아닌 것으로 보장되고(0은 허용 가능) 목표에 대한 가장 저렴한 경로의 비용보다 결코 크지 않은 경우 휴리스틱이 허용된다.

  • 에지 비용이 변경되면 노드의 일부만 다시 확장하면 되므로 LPA star 는 A star 보다 성능이 뛰어나다(후자가 처음부터 실행된다고 가정).

출처: https://en.wikipedia.org/wiki/Lifelong_Planning_A*

5. D* 알고리즘 구현

• Pseudo code

while (!openList.isEmpty()) {
    point = openList.getFirst();
    expand(point);
}

• Expend

void expand(currentPoint) {
    boolean isRaise = isRaise(currentPoint);
    double cost;
    for each (neighbor in currentPoint.getNeighbors()) {
        if (isRaise) {
            if (neighbor.nextPoint == currentPoint) {
                neighbor.setNextPointAndUpdateCost(currentPoint);
                openList.add(neighbor);
            } else {
                cost = neighbor.calculateCostVia(currentPoint);
                if (cost < neighbor.getCost()) {
                    currentPoint.setMinimumCostToCurrentCost();
                    openList.add(currentPoint);
                }
            }
        } else {
            cost = neighbor.calculateCostVia(currentPoint);
            if (cost < neighbor.getCost()) {
                neighbor.setNextPointAndUpdateCost(currentPoint);
                openList.add(neighbor);
            }
        }
    }
}

• check for raise

boolean isRaise(point) {
    double cost;
    if (point.getCurrentCost() > point.getMinimumCost()) {
        for each(neighbor in point.getNeighbors()) {
            cost = point.calculateCostVia(neighbor);
            if (cost < point.getCurrentCost()) {
                point.setNextPointAndUpdateCost(neighbor);
            }
        }
    }
    return point.getCurrentCost() > point.getMinimumCost();
}

출처 : https://en.wikipedia.org/wiki/D*