다익스트라 알고리즘

1. 다익스트라 알고리즘이란?

• 다익스트라 알고리즘(Dijkstra algorithm)은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.

• 다익스트라의 원래 알고리즘은 두 꼭짓점 간의 가장 짧은 경로를 찾는 알고리즘이지만, 더 일반적인 변형은 한 꼭짓점을 "소스" 꼭짓점으로 고정하고 그래프의 다른 모든 꼭짓점까지의 최단경로를 찾는 알고리즘으로 최단 경로 트리를 만드는 것이다.

• 최단 경로 알고리즘은 네트워크 라우팅 프로토콜에서 널리 이용되며, 특히 IS-IS (Intermediate System to Intermediate System)와 OSPF(Open Shortest Path First)에서 주로 사용된다.

2. 알고리즘

• 시작할 꼭짓점은 초기점으로, 꼭짓점 Y의 거리를 초기점에서 Y까지의 거리로 정의한다. 다익스트라 알고리즘은 초기 거리 값을 부여하고, 단계를 거듭하며 개선시킬 것이며, 이 개선시키는 것을 간선 완화(edge relaxation)이라고 한다.

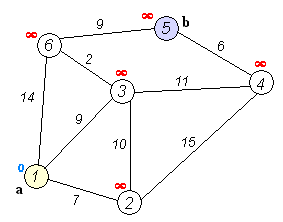
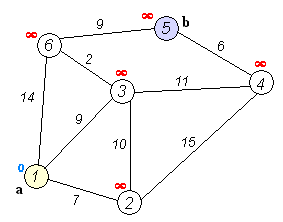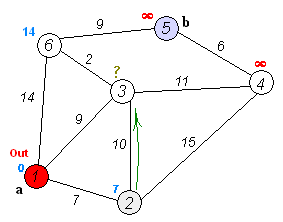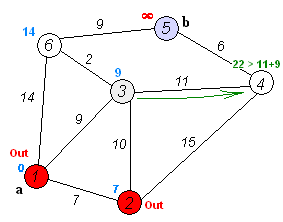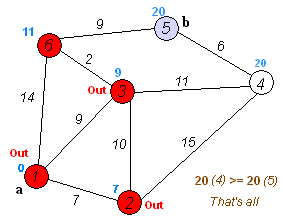
  1. 모든 꼭짓점을 미방문 상태로 표시한다. 미방문 집합이라는 모든 미방문 꼭짓점의 집합을 만든다.

  2. 모든 꼭짓점에 시험적 거리 값을 부여한다: 초기점을 0으로, 다른 모든 꼭짓점을 무한대로 설정한다. 초기점을 현재 위치로 설정한다.

  3. 현재 꼭짓점에서 미방문 인접 꼭짓점을 찾아 그 시험적 거리를 현재 꼭짓점에서 계산한다. 새로 계산한 시험적 거리를 현재 부여된 값과 비교해서 더 작은 값을 넣는다. 예를 들어, 현재 꼭짓점 A의 거리가 6이라고 표시되었고, 인접 꼭짓점 B로 연결되는 변의 길이가 2라고 한다면, A를 통한 B까지의 거리는 6 + 2 = 8이 된다. 이전의 B까지의 거리가 8보다 컸다면 8로 바꾸고, 그렇지 않다면 그대로 놔둔다.

  4. 만약 현재 꼭짓점에 인접한 모든 미방문 꼭짓점까지의 거리를 계산했다면, 현재 꼭짓점을 방문한 것으로 표시하고 미방문 집합에서 제거한다. 방문한 꼭짓점은 이후에는 다시 방문하지 않는다.

  5. 두 꼭짓점 사이의 경로를 찾는 경우: 도착점이 방문한 상태로 표시되면 멈추고 알고리듬을 종료한다.

  6. 완전 순회 경로를 찾는 경우: 미방문 집합에 있는 꼭짓점들의 시험적 거리 중 최솟값이 무한대이면 이는 출발점과 미방문 집합 사이에 연결이 없는 경우이므로 멈추고 알고리즘을 종료한다.

  7. 아니면 시험적 거리가 가장 작은 다음 미방문 꼭짓점을 새로운 "현재 위치"로 선택하고 3단계로 되돌아간다.

3. 구현 (우선순위 큐 사용)

1  function Dijkstra(Graph, source):
2      dist[source] ← 0                                    
		// 초기화
3
4      create vertex set Q
5
6      for each vertex v in Graph:
7          if v ≠ source
8              dist[v] ← INFINITY                          
		// 소스에서 v까지의 아직 모르는 길이
9          prev[v] ← UNDEFINED                             
		// v의 이전 노드
10
11         Q.add_with_priority(v, dist[v])
12
13
14     while Q is not empty:                          
		// 메인 루프
15         u ← Q.extract_min()                         
			// 최고의 꼭짓점을 제거하고 반환한다
16         for each neighbor v of u:              
			// Q에 여전히 남아 있는 v에 대해서만
17             alt ← dist[u] + length(u, v)
18             if alt < dist[v]
19                 dist[v] ← alt
20                 prev[v] ← u
21                 Q.decrease_priority(v, alt)
22
23     return dist, prev

출처 : https://ko.wikipedia.org/wiki/%EB%8D%B0%EC%9D%B4%ED%81%AC%EC%8A%A4%ED%8A%B8%EB%9D%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

4. 다익스트라 알고리즘 vs A* 알고리즘

1. 목표점

   • 다익스트라는 시작점으로부터 나머지 정점들까지의 최단거리를 구한다.

   • A* 는 시작점이 정해지고, 목표점이 정해지면 두 개의 최단 거리를 구한다.

2. 남은 거리 고려

   • 다익스트라는 시작점에서 정점에 이르는 최단 거리만을 고려.
     목적 정점이 없기에 남은 거리를 구할 수도 없다.

   • A* 는 고려한다.

3. 최적 경로

   • 다익스트라는 임의의 시작점으로부터 시작하여 모든 정점을 탐색. 최적 경로를 보장하지 않는다.

   • A* 는 시작지점부터 목표 지점까지의 휴리스틱 함수를 통해 추정하여 점수를 매기고, 그 점수를 바탕으로 빠른 탐색을 한다. 최적 경로의 근사값을 보장한다.

출처 : https://hyo-ue4study.tistory.com/m/195