4 고급 설계 및 분석 기술
개요
이 단원에서 다루는 중요한 세 가지: 동적 프로그래밍 (15 단원), 탐욕 알고리듬 (16 단원), 분할 상환 분석 (17 단원).
동적 프로그래밍은 보통 최적의 해를 구하는 문제를 풀 때, 그 도중에 몇 가지 선택을 해야하는 경우 적합함. 이때 보통 선택지가 전부 동일한 하위 문제인 경우임.
탐욕 알고리듬도 동적 프로그래밍이랑 유사함. 다만, 전역 최적에 대한 선택이 아닌, 지역 최적에 대한 선택을 함.
분할 상환 분석을 통해 비슷한 연산을 연속으로 처리하는 몇몇 알고리듬을 분석함. 연산의 유계를 독립적으로 따로 따로 구하는 것이 아닌, 모든 연속된 연산의 실제 비용에 유계를 제공하는 것이 분할 상환 분석. 장점이라면 몇몇 연산은 비싸더라도, 또 몇몇 연산은 싸다는 것. 즉, 많은 연산이 최악의 경우 시간보다는 빠르게 돈다는 것임. 단순 분석 도구일 뿐만 아니라 알고리듬 설계 철학이기도 함. 세 가지 분할 상환 분석 방법 소개할 것.
15. 동적 프로그래밍
분할 정복 방법처럼 하위 문제로 나눠서 해법을 구한다는 건 동일함. (여기서 "프로그래밍"이라는 건 코드를 짠다는 그 행위가 아니라, 도표 방법을 사용한다는 의미임) 하지만 동적 프로그래밍은 하위 문제가 겹칠 때의 경우라는 점에서 분할 정복과는 다름. 동일한 하위 문제가 존재할 때 분할 정복하면 똑같은 하위 문제를 여러 번 반복하니 오히려 비효율적임. 동적 프로그래밍은 이런 하위 문제 하나를 해결하면, 이걸 도표에 기록해놓고, 나중에 또 필요할 때 연산할 필요 없이 기록된 도표만 참고해서 값을 바로 받아올 수 있음.
보통 동적 프로그래밍을 최적화 문제 optimization problem에 사용함. 당연히 해법이 여러 개가 될 수 있음. 이때 제일 최적(최소 혹은 최대)의 값을 갖는 해법을 구하는 것이 목표임. 이때 이걸 한 최적해라고 부르지, 유일한 최적해라고 부르지는 않음.
동적 프로그래밍 알고리듬 개발할 땐 다음 네 단계를 따름:
- 최적 해의 구조의 특성 파악
- 최적 해의 값을 재귀적으로 정의
- 최적 해의 값을 보통 상향식으로 계산
- 최적 해를 계산한 정보로부터 도출
1-3 단계가 동적 프로그래밍 해법 구하는 기본 단계. 해법의 값만 필요하고 해법 자체가 필요 없으면 4번 단계는 생략해도 됨.
15.1. 막대 자르기
철골을 자르는 간단한 문제. Serling사(社)에서 긴 철골을 더 짧은 철골로 자른 뒤 판매하려고 함. 자르는 비용은 고려 X. 이때 어떤 방법으로 철골을 잘라야 제일 수익이 남는지를 판단해야함.
철골의 길이가 i 인치일 때의 가격을 pi 달러라고 가정. 길이는 언제나 정수라고 가정. 가격표 예시:
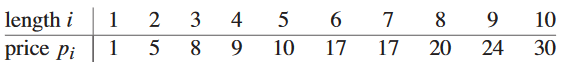
막대 자르기 문제 rod-cutting problem은 다음과 같음. 길이가 n 인치인 막대에 대해 i = 1, 2, …, n에 대한 가격 pi를 나타낸 가격표가 주어졌을 때, 막대를 자르고 판매할 때 얻을 수 있는 최고 수익 rn를 구하라. 참고로 pn의 값이 충분히 높아 최적의 해라면, 아예 자르지 않는 게 제일 수익성이 좋다는 의미임.
n = 4인 경우:
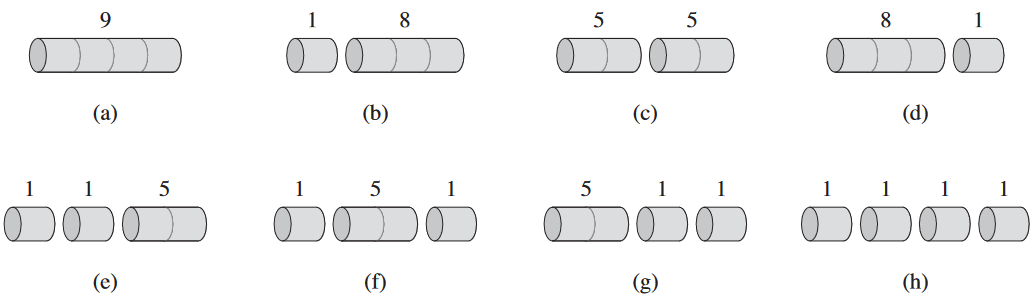
이 경우 두 개의 2 인치로 나누는게 제일 수익성이 좋음.
막대를 2n - 1 가지의 방법으로 자를 수 있음. 이때 최적의 해가 막대를 1 ≤ k ≤ n인 k 개의 부분으로 자른다면 최적의 분할은 다음과 같음:
n = i1 + … + ik
이때 ik는 각 부분의 길이임. 이를 통해 최고 수익을 구할 수 있음:
rn = pi1 + pi2 + … + pik
이걸 단순화하면 n ≥ 1일 때 rn의 값은 더 짧은 막대에 대한 최대 수익에 대하여 표현 가능함:
rn = max(pn, r1 + rn - 1, r2 + rn - 2, …, rn - 1 + r1)
pn은 분할 안하는 경우, ri + rn - i는 막대를 i와 n - i로 일단 나눠놓고, 나눠진 각 막대에 대한 최대 수익을 더한 것. 어떤 i와 n - i의 조합이 최적인지 모르니 일일이 다 확인은 해야 함. 만약 최적이 아니면 그냥 pn 뽑으면 되는 거고.
이때 크기만 i로 줄어들 뿐이지 해결할 하위 문제는 사실상 상위 문제랑 동일함. 어차피 각 문제는 막대를 둘로 나누고, 이걸 독립된 하위 문제로 처리하는 것 뿐임. 그리고 어차피 하위 문제가 최적이어야 상위 문제도 최적이 됨. 이런 경우를 최적 하위 구조 optimal substructure를 갖는다고 함. 즉, 최적의 해를 구하는 문제가 있을 때, 이의 해결법이 본래 문제와 연관된, 서로 독립적으로 처리될 수도 있는 하위 문제의 최적의 해를 구하는 형태임.
위의 식을 단순화하자면 둘을 나눠서 따로 보지 말고, 앞에 건 내비두고, 뒤에 것만 분할하자는 것임. 이러면 아예 안 나누는 경우를 i = n이고 나머지는 크기가 0이므로 r0 = 0인 경우로 둘 수 있음:
rn = max1≤i≤n(pi + rn - i)
이 공식에 따르면 최적 해는 두 개의 하위 문제가 아니라 하나의 하위 문제에 대한 식이 됨.
재귀적 하향식 구현
CUT-ROD(p, n)
1 if n == 0
2 return 0
3 q = -∞
4 for i = 1 to n
5 q = max(q, p[i] + CUT-ROD(p, n - i))
6 return q가격 배열 p[1..n]와 정수 n을 입력으로 받아 길이 n인 막대의 최대 수익을 반환함.
이거 n이 충분히 커지면, n = 40만 돼도 사실 엄청 오래 걸리는 알고리듬임.
왜 비효율적이냐면 CUT-ROD가 자기 자신을 같은 매개 변수 값에 대해 반복적으로 호출하기 때문임. n = 4의 경우 호출 그림:
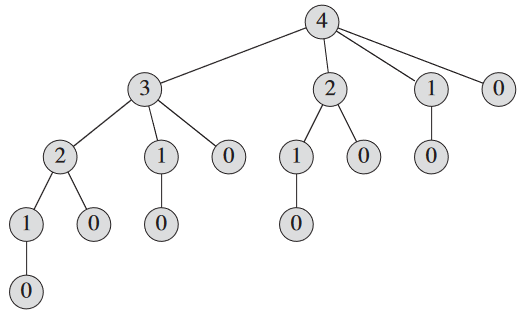
실행 시간 T(n) 분석해보면 T(0) = 1,
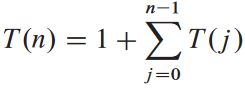
첫항 1은 뿌리에서 호출한 경우를 의미, T(j)는 j = n - i일 때 CUT-ROD(p, n - i)을 호출할 때 발생한 호출 총 횟수(재귀 호출 포함).
CUT-ROD의 실행 시간은
T(n) = 2n
이므로 기하급수적으로 증가함.
사실 CUT-ROD는 명시적으로 2n - 1 가지의 경우의 수를 고려하는데 당연히 잎이 2n - 1 가지일 것임.
동적 프로그래밍으로 최적의 막대 자르는 법 구하기
이제 하위 문제를 오로지 한 번만 처리하고, 이 결과를 저장하는 식으로 바꾸면 효율적으로 바꿀 수 있음. 즉, 동적 프로그래밍은 추가적인 메모리를 통해 실행 시간을 줄여주므로 시간-메모리 트레이드오프 time-memory trade-off라 부름. 지수 시간 걸리던데 다항식 수준으로 급격하게 줄어듦. 동적 프로그래밍은 서로 다른 하위 문제가 입력 크기에 대해 다항일 때 다항 실행 시간을 가짐.
보통 동적 프로그래밍은 두 가지 동일한 방법으로 구현함.
첫번째는 메모이제이션을 통한 하향식 방법 top-down with memoization임. 여기선 재귀적으로 작성을 할 때, 각 하위문제의 결과를 따로 저장해놓는 것임(주로 배열이나 해시 테이블에 저장함). 나중에 하위 문제의 결과가 필요하면 이 저장소에 기존 자료가 있는지만 확인하고 갖다 쓰기만 하면 됨. 이런 걸 재귀 호출을 암기했다 memoized고 함.
두번째는 상향식 방법 bottom-up method임. 보통 하위 문제의 "크기"와 같은 자연적인 개념에 의존함. 즉, 한 문제를 푸려면 해당 문제보다 "규모가 작은" 하위 문제를 푸는 것이라는 뜻임. 우선 하위 문제를 크기 순으로 정렬한 뒤 작은 것부터 풀어가는 것임. 그럼 작은 문제를 이미 풀었을테니 큰 문제 풀 땐 이미 풀어놓은 작은 애들 갖다 쓰면 됨.
어차피 점진적인 실행 시간은 둘 다 같음. 하지만 가끔 하향식이 실제로 모든 가능한 하위 문제를 재귀적으로 처리하지 않는 경우가 발생하긴 함. 하향식이 주로 더 나은 성능을 보임. 호출 부담도 적고.
메모이제이션을 추가한 하향식 CUT-ROD 코드임:
MEMOIZED-CUT-ROD(p, n)
1 r[0..n]라는 새 배열 생성
2 for i = 0 to n
3 r[i] = -∞
4 return MEMOIZED-CUT-ROD-AUX(p, n, r)MEMOIZED-CUT-ROD-AUX(p, n, r)
1 if r[n] ≥ 0
2 return r[n]
3 if n == 0
4 q = 0
5 else q = -∞
6 for i = 1 to n
7 q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n - i, r))
8 r[n] = q
9 return q우선 MEMOIZED-CUT-ROD에서 새 보조 배열 r[0..n]을 만들고, 값 미정이라는 의미로 -∞를 부여함(어차피 최대 수익은 음수가 아닌 값일테니). 이후 도우미 함수 MEMOIZED-CUT-ROD-AUX 호출.
MEMOIZED-CUT-ROD-AUX 그냥 CUT-ROD에 암기 부분만 추가되었을 뿐임.
상향식은 더 간단함:
BOTTOM-UP-CUT-ROD(p, n)
1 r[0..n]이라는 배열 생성
2 r[0] = 0
3 for j = 1 to n
4 q = -∞
5 for i = 1 to j
6 q = max(q, p[i] + r[j - i])
7 r[j] = q
8 return r[n]하위 문제를 순서대로 처리함: 크기가 i인 문제가 크기가 j인 하위 문제보다 더 "작다"는 순이므로, j = 0, 1, …, n 순으로 처리됨.
상향식 하향식 둘 다 실행 시간은 점진적으로 같음. BOTTOM-UP-CUT-ROD의 실행 시간은 이중 for문에 의해 Θ(n2)임. MEMOIZED-CUT-ROD도 마찬가지임.
하위 문제 그래프
동적 프로그래밍 문제를 다룰 땐 하위 문제의 집합이 무엇인지, 그리고 하위 문제가 서로 어떤 관계를 갖는 지를 이해해야 함.
이에 대한 정보를 제공하는 것이 바로 하위 문제 그래프 subproblem graph임. 아래 그림이 n = 4에 대한 막대 자르기 문제의 하위 문제 그래프:
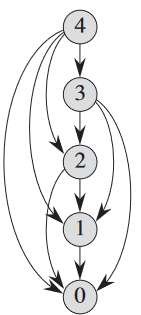
하위 문제 그래프는 하위 문제 x의 최적의 해를 구하는게 하위 문제 y의 최적의 해를 구하는데 직접적 영향을 주면, 하위 문제 x에 대한 정점에서부터 하위 문제 y를 가리키는 방향성 모서리를 그림. 이런 하위 문제 그래프를 하향식 재귀법의 재귀 트리의 "축소"된 버전이라고 생각하면 됨. 서로 같은 노드를 하나의 정점으로 퉁치고, 부모에서 자식으로의 나머지를 방향성 있게 수정하면 됨.
상향식 방법의 경우 주어진 하위 문제 x에 대해서 x를 풀기 전에 x에 인접한 하위 문제 y를 먼저 푸는 것임. 이때 22 단원의 용어를 빌리자면 하위 문제 그래프의 정점을 "역 위상 정렬" 혹은 "전이의 위상 정렬"(22.4절 참고)된 순서라고 부름. 다시 말해 자신이 의존하는 하위 문제를 전부 해결하지 못하면 자신도 해결 못한다는 뜻임. 22 단원의 개념을 계속 빌리자면, 하향식은 하위 문제 그래프에 대한 "깊이 우선 탐색"이라 볼 수 있음(22.3절 참고).
하위 문제 그래프 G = (V, E)의 크기를 통해 동적 프로그래밍 알고리듬의 실행 시간 구할 수 있음. 어차피 각 하위 문제는 한 번만 처리하니까, 결국 실행 시간은 각 하위 문제를 해결하는데 걸리는 시간들의 합임. 보통 하위 문제를 해결하는데 걸리는 시간은 해당 정점의 계수(밖으로 향하는 모서리의 수)에 비례하고, 하위 문제의 개수는 하위 문제 그래프의 정점의 수와 동일함. 상식적으로 동적 프로그래밍의 실행 시간은 정점과 모서리의 개수에 선형적임.
해 재구축하기
우리가 구한 값은 최적 해의 값이지 실제 해, 즉 나눠진 막대 크기들을 의미하는 것이 아님. 그렇기에 최적의 값 뿐만 아니라 이 값에 해당하는 선택지도 기록을 해야함.
각 막대 크기 j에 대해 최대 수익 rj 뿐만 아니라 자를 첫번째 부분의 최적의 크기를 의미하는 sj도 반환하는BOTTOM-UP-CUT-ROD 확장판:
EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
1 r[0..n], s[0..n]이라는 배열 생성
2 r[0] = 0
3 for j = 1 to n
4 q = -∞
5 for i = 1 to j
6 if q < p[i] + r[j - i]
7 q = p[i] + r[j - i]
8 s[j] = i;
9 r[j] = q
10 return r and s가격표 p, 막대 크기 n에 대해서 최적의 분할 결과를 출력하는 함수:
PRINT-CUT-ROD-SOLUTION(p, n)
1 (r, s) = EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
2 while n > 0:
3 print(s[n])
4 n = n - s[n]위에서의 예시를 실제로 실행해보면 다음 결과가 나옴:
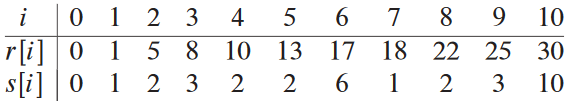
15.2. 연쇄행렬 최소곱셈
n 개의 행렬 <A1, …, An>을 다음 순서로 곱한다고 가정:
A1A2…An
결국 이걸 괄호를 어떻게 치느냐에 따라 곱셈 순서가 결정됨. 어차피 결합 법칙 때문에 어떻게 치든 결과는 같음. 행렬의 곱셈 결과가 하나의 행렬이거나 괄호로 둘러 싸인 두 개의 완전히 괄호로 둘러싸인 행렬의 곱일 경우, 완전히 괄호로 둘러 쌓임 fully parenthesized이라고 함. n = 4일 경우 다섯 가지 방법으로 완전히 괄호로 둘러 쌀 수 있음:
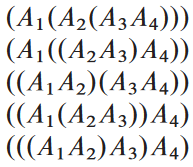
어떤 순서로 곱하느냐에 따라 곱셈 비용 천차만별임. 우선 두 행렬 곱할 때의 비용 확인. rows와 columns는 각각 행렬의 행 개수, 열 개수임:
MATRIX-MULTIPLY(A, B)
1 if A.columns ≠ B.rows
2 error "incompatible dimensions"
3 else A.rows × B.columns인 행렬 C 생성
4 for i = 1 to A.rows
5 for j = 1 to B.columns
6 c<sub>ij</sub> = 0
7 for k = 1 to A.columns
8 c<sub>ij</sub> = c<sub>ij</sub> + a<sub>ik</sub> ⋅ b<sub>kj</sub>
9 return CA와 B가 서로 연산 가능 compatible해야 곱할 수 있음. A가 p × q 행렬, B가 q × r 행렬이면 결과 C는 p × r 행렬. 즉, 총 스칼라곱 수는 pqr.
이게 순서에 따라 총 곱셈 수에 차이가 나서 성능 차이가 남.
그러므로 연쇄행렬 최소곱셈 문제 matrix-chain multiplication problem을 다음과 같이 정의: n 개의 행렬로 이루어진 연쇄행렬 <A1, …, An>이 주어졌을 때 Ai의 차원은 pi - 1 × pi이며, A1A2…An을 최소한의 스칼라 곱으로 구할 수 있게 완전히 괄호로 싸는 문제.
참고로 실제 곱하는 건 아니고, 그냥 어떤 순서로 곱해야 제일 덜 곱하는지만 알아내는 것임. 보통 곱하기 전에 순서를 먼저 정하는게 더 성능이 좋은 편임.
괄호 치는 경우의 수
위에서 했던 것처럼 당연히 괄호를 치는 모든 경우의 수를 일일이 확인하는 건 비효율적임을 볼 것. 크기 n의 연쇄행렬을 괄호를 치는 모든 경우의 수를 P(n)이라고 정의:
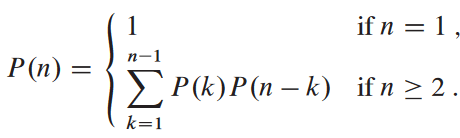
이런 점화식은 카탈랑 수 Catalan number라 부르며, Ω(4n/n3/2)의 속도로 증가함. 여튼 기하급수적임.
동적 프로그래밍 적용하기
네 가지 단계 적용:
1. 최적 괄호 구조
대충 Ai..j가 Ai…Aj라고 가정. 이걸 괄호를 치려면 i ≤ k < j인 k에 대해서 Ak와 Ak + 1 사이를 기준으로 나눠야함. 결국 Ai..j의 비용은 Ai..k의 비용과 Ak+1..j을 합한 것임.
결국 이때 이 결과가 최적이려면 Ai..k이 최적의 분할이어야함. Ak+1..j도 마찬가지.
즉, 현재가 최적이려면 하위 문제가 최적이야함. 그러므로 괄호를 놓을 수 있는 모든 경우의 수에 대해 최적인지 아닌지 다 일일이 확인해야함.
2. 재귀적 해법
이제 최적의 해를 하위 문제에 대해 재귀적으로 구함. 여기서 하위 문제라는 건 1 ≤ i ≤ j ≤ n인 Ai..j의 최소 비용 구하기임. m[i, j]가 최소 스칼라곱 횟수를 의미한다고 하면 결국 최상위 문제 A1..n에 대해 m[1, n]이 정답임.
다음과 같이 m[i, j]를 재귀적으로 구할 수 있음. i = j면 Ai..i란 소리니까 비용 없으니 m[i, i] = 0임. i < j일 경우 1 단계의 최적의 해를 기반으로 구하면 됨. 최적의 해로 k에서 분할했다고 가정. 그러면 m[i, j]의 값은 하위 문제 Ai..k와 Ak+1..j의 각 최소 비용에 이 두 행렬 간의 곱 비용을 더한 값임. 즉, 다음과 같음:
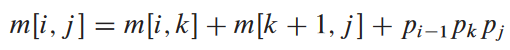
우리가 k의 값을 이미 알고 있다고 가정한 공식임. k의 값을 따로 구해야함:
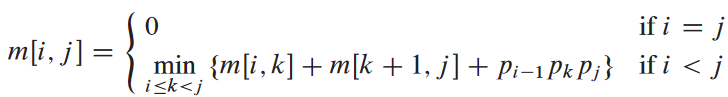
최적 해의 값을 구할 수는 있어도, 실제 최적 해를 알 수는 없음. 그러므로 위의 공식에서 min으로 구한 k의 값을 따로 s[i, j]에 저장해주어야함.
3. 최적 비용 계산
상대적으로 적은 서로 다른 하위 문제들을 갖고 있음: 하나는 i와 j의 값을 정하는 것이므로 (n choose 2) + n = Θ(n2). 이때 하위 문제들이 서로 겹칠 수도 있어 동적 프로그래밍을 사용하는 두번째 이유(첫번째는 내재적인 최적 구조).
이걸 재귀적으로 하지 말고, 도표로, 상향식으로 처리.
아래 MATRIX-CHAIN-ORDER 함수에 적어놨음:
MATRIX-CHAIN-ORDER(p)
1 n = p.length - 1
2 새 도표 m[1..n, 1..n]와 s[1..n - 1, 2..n] 생성
3 for i = 1 to n
4 m[i, i] = 0
5 for l = 2 to n // l이 연쇄 길이
6 for i = 1 to n - l+ 1
7 j = i + l - 1
8 m[i, j] = ∞
9 for k = i to j - 1
10 q = m[i, k] + m[k + 1, j] + p_i-1 p_k p_j
11 if q < m[i, j]
12 m[i, j] = q
13 s[i, j] = k
14 return m and s