7. 퀵 정렬
최악의 경우 Θ(n2). 그럼에도 평균의 경우에서 Θ(n lg n)이고, 여기에 숨은 상수도 값이 작아서 상당히 효율적임. 게다가 공간 복잡도도 Θ(1)고, 특히 가상 메모리 환경에서 잘 돎.
7.1. 퀵 정렬 설명
퀵 정렬도 합병 정렬도 분할정복 패러다임. 부분열 A[p..r]에 대한 분할정복 과정:
- 분할. 배열 A[p..r]를 두 부분열 A[p..q-1], A[q+1..r]로 나눔(하나가 비어있을 수도 있음). 이때 전자의 원소가 A[q]보다 적거나 같아야 하며, A[q]는 A[q+1..r]과 작거나 같아야 함. q의 값은 분할 과정에서 얻음.
- 점령. 퀵 정렬 재귀 호출로 각 부분열 정렬
- 결합. 부분열들이 이미 정렬되어 있으니 결합 따로 필요없음. 원본 배열 A[p..r]은 이미 정렬된 상태.
다음 과정에 따르면 됨:
QUICKSORT(A, p, r)
1 if p < r
2 q = PARTITION(A, p, r)
3 QUICKSORT(A, p, q - 1)
4 QUICKSORT(A, q + 1, r)배열 A 하나 정렬하려면 QUICKSORT(A, 1, A.length) 호출하면 됨.
배열 분할하기
(역: 여기서 분할은 partition. 분할정복의 분할divide과는 다름)
알고리듬의 핵심인 PARTITION 절차로, 부분열 A[p..r]를 재배치:
PARTITION(A, p, r)
1 x = A[r]
2 i = p - 1
3 for j = p to r - 1
4 if A[j] ≤ x
5 i = i + 1
6 exchange A[i] with A[j]
7 exchange A[i + 1] with A[r]
8 return i + 1위의 코드가 도는 실제 예시:
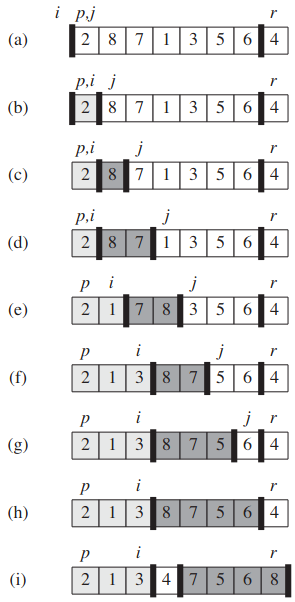
언제나 x = A[r]를 기준 pivot 원소로 선택해서 얘를 기준으로 부분열을 분할함. 3-6번 줄의 for 문에서 다음 속성 만족:
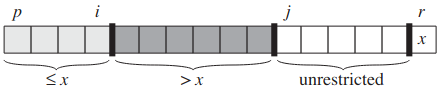
이 속성이 바로 우리가 설정할 루프 불변성:
3-6번 줄의 루프 시작 직전마다 임의의 배열 색인 k에 대해:
- 만약 p ≤ k ≤ i라면, A[k] ≤ x
- 만약 i + 1 ≤ k ≤ j - 1라면, A[k] > x
- 만약 k = r이라면 A[k] = x
j와 r - 1 사이는 어떤 경우에도 속하지 않음. 딱히 기준 x랑 관계 없으니까.
이제 루프 불변성이 참임을 보이면 됨:
- 초기화. 루프 시작 전, i = p - 1, j = p이 일 때. p와 i 사이에 값이 없고, i + 1와 j - 1 사이에도 값이 없으므로 자명하게 루프 불변성 만족. 1번 줄의 할당이 세번째 조건 만족.
- 유지보수. 아래 그림에서처럼 4번 줄의 테스트에 따라 나온 두 경우 고려. A[j] > x 즉 a. 땐 증가만 하면 되고, 이후에 j 증가시킴. A[j] ≤ x 즉 b에선 i 증가시키고 A[i]와 A[j] 교체하고 j 증가. 교체했으니 A[i] ≤ x이므로 1번 조건 만족. 비슷하게 A[j - 1] > x인데, 루프 불변성에 의해 x보다 크거나 같음.
- 종료. 종료 시, 즉 j = r. 배열의 각 원소가 루프 불변성의 세 가지 중 하나 만족. 즉 x보다 작거나 같거나, x보다 크거나, x만 갖는 경우.
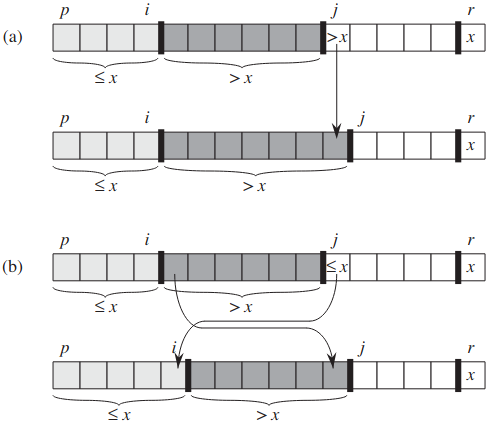
PARTITION의 마지막 두 줄에서는 기준 원소와 x보다 큰 최서단 원소와 교체해서 기준을 올바른 위치로 옮겨줌. PARTITION의 출력은 이제 분할하기 위한 기본 조건을 만족. QUICKSORT의 2번 줄 이후 A[q]는 A[q + 1..r]의 모든 원소보다 작게 됨.
부분열 A[p..r]에 대한 PARTITION의 실행 시간은 Θ(n). 이때 n = r - p + 1.
7.2. 퀵 정렬의 성능
퀵 정렬의 성능은 분할이 얼마나 균형적인지에 달림. 즉, 어떤 원소를 기준으로 삼는지임. 균형 잡히면 알고리듬이 점진적으로 합병 정렬만큼 빠름. 균형 잡히지 않으면 삽입 정렬만큼 느릴 수 있음.
최악의 경우 분할
최악의 경우는 분할의 결과로 부분 문제가 각각 n - 1 개 원소의 문제와 0 개 원소의 문제로 나뉠 때. 이게 모든 경우에 발생한다고 가정. 우선 분할은 Θ(n). 크기 0인 배열에서 재귀 호출에선 아무 일도 없으니 T(0) = Θ(1). 즉, 실행 시간 점화식:
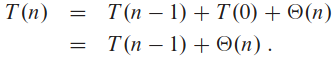
직관적으로봐도 대충 Θ(n2)인 게 보임.
최악의 경우는 배열이 이미 정렬 됐을 때 발생함. 이때 삽입 정렬은 O(n)이었음.
최고의 경우 분할
가장 고르게 분할할 경우 n/2 씩으로 분할됨. 하나는 ⌊n/2⌋, 나머지는 ⌈n/2⌉ - 1의 크기를 가짐. 이 경우의 점화식:
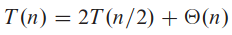
대충 바닥/천장 함수 무시하고 보면 마스터 정리에 의해 T(n) = Θ(n lg n)인 걸 알 수 있음. 매 재귀마다 고르게 분할되면 점진적으로 더 빠른 알고리듬 얻을 수 있음.
균형 분할
평균 실행 시간은 최고의 경우에 좀 더 가까움. 왜 그런지는 균형이 어떤 영향을 주는지를 이해해야 함.
예를 들어 분할 알고리듬이 언제나 9:1 비율의 분할을 한다고 가정:
T(n) = T(9n/10) + T(n/10) + cn
아래 그림 참고.
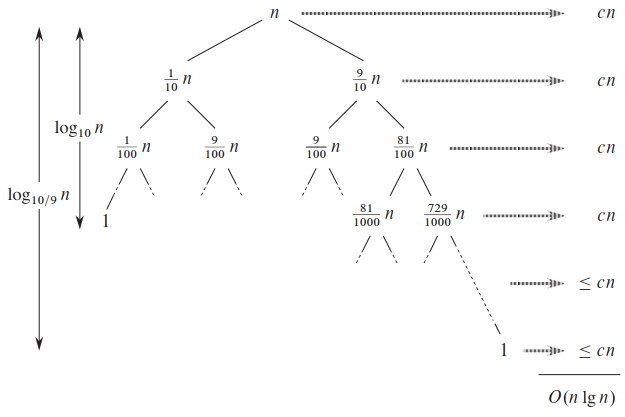
바닥 log10 n = Θ(lg n)에 닿을 때까지 매 단계마다 최대 cn 비용. 각 재귀마다 9:1 비율로 분할되므로 균형 잡히지 않아 보이겠지만 결국 O(n lg n)으로 돎. 심지어 99:1도 그럼. 대충 상수 constant 비율로 깊이가 Θ(lg n)이고, 각 단계의 비용이 O(n)인 재귀 트리를 분할하면 실행 시간 O(n lg n)임.
평균적인 경우에 대한 직관
퀵 정렬의 무작위적인 행동을 이해하려면 얼마나 자주 다양한 입력을 받는지를 알아야 함. 퀵 정렬의 행동은 주어진 입력의 실제 값이 아니라, 값들 사이의 상대적 순서에 따라 달라짐.
무작위 입력 배열에 퀵 정렬 적용하면 직관적으로 보면 분할이 매 단계마다 똑같이 작동하지 않을 것임을 알 수 있음. 적당히 어떻게 분할해야 균형 잡힌 분할인지 대충 다 앎.
평균적인 경우 PARTITION이 "좋"거나 "나쁜" 분할이 섞여져서 진행됨. 그리고 이 경우들이 무작위로 분배되어 있음. 아래 그림에서 볼 수 있듯이 최고의 경우와 최악의 경우가 섞여서 나온다고 가정:
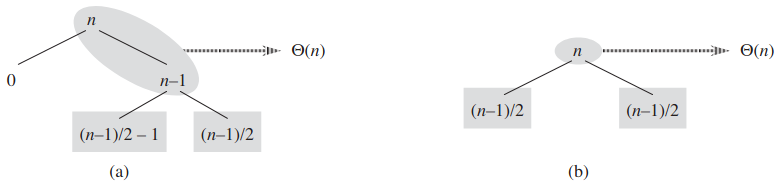
크기가 0인 부분열의 경우 경계 확인 비용이 1이라고 친다고 가정.
나쁜 경우 다음에 좋은 경우가 올 땐 크기 0, (n - 1/2 - 1, (n - 1)/2의 크기를 갖는 부분열 세 개가 나옴. 이때 분할 비용은 Θ(n) + Θ(n - 1) = Θ(n). 이게 b에서 한 단계를 분할한 비용 Θ(n)보다 더 나쁘지도 않음. 근데 후자는 균형잡인 경우임. 직관적으로 보면 나쁜 경우의 분할 비용 Θ(n - 1)이 좋은 경우의 비용 Θ(n)에 포함되므로, 결과적인 분할은 좋은 경우로 쳐짐. 그러므로 좋은 경우와 나쁜 경우가 돌아가면서 나올 경우 마치 좋은 경우처럼 작동해서, O(n lg n)임. 물론 상수가 조금 더 크긴 함.
7.3. 무작위 퀵 정렬
평균 경우 분석할 땐 입력 숫자들의 순열이 비슷하다고 가정했음. 실무에서는 언제나 이 가정이 옳은지는 모름. 모든 입력에 대해 괜찮은 성능을 위해 무작위를 추가해줄 수도 있음. 입력이 충분히 클 때 사용하는 퀵 정렬이라고 많이들 말함.
입력을 명시적으로 순열로 배치해서 무작위 적용했었음. 퀵 정렬에서는 무작위 샘플링 random sampling이라는 다른 무작위 방법 사용. A[r]를 언제나 기준으로 삼지 말고, A[p..r] 안에서 임의로 기준을 삼자는 것. 그러면 평균적으로 배열도 균형잡힐 것임.
몇 가지만 변경해주면 됨:
RANDOMIZED-PARTITION(A, p, r)
1 i = RANDOM(p, r)
2 exchange A[r] with A[i]
3 return PARTITION(A,p ,r)RANDOMIZED-QUICKSORT(A, p, r)
1 if p < r:
2 q = RANDOMIZED-PARTITION(A, p, r)
3 RANDOMIZED-QUICKSORT(A, p, q - 1)
4 RANDOMIZED-QUICKSORT(A, q + 1, r)7.4. 퀵 정렬 분석
좀 더 수학적으로 엄격하게 알고리듬을 분석해볼 것.
7.4.1. 최악의 경우 분석
7.2절에서 퀵 정렬의 최악의 경우 실행 시간은 Θ(n2)라 했음.
4.3절의 치환법을 바탕으로 퀵 정렬의 실행 시간이 O(n2)임을 보일 수 있음.
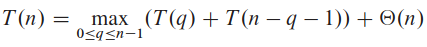
q의 범위는 0에서 n - 1. T(n) ≤ cn2이라 가정.
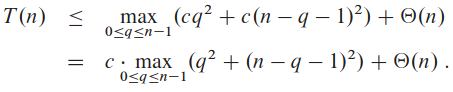
q2 + (n - q - 1)2이 끝점 모두에서 매개변수의 범위 0 ≤ q ≤ n - 1에서 최대를 달성함. 이를 증명하려면 표현식의 q에 대한 이차도함수이 양임을 보이면 됨. 이러면 범위 max0≤q≤n-1(q2 + (n - q - 1)2) ≤ (n - 1)2 = n2 - 2n + 1를 얻게 됨.
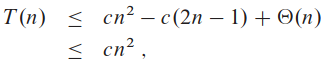
이러면 상수 c를 구할 수 있으므로 c(2n - 1) 항이 Θ(n) 계수를 지배함. 그러므로 T(n) = O(n2). 7.2절에서 봤듯이 특정 경우에 Ω(n2)를 만족하는 경우, 즉 불균형한 경우가 있었음.
7.4.2. 예상 실행 시간
이미 RANDOMIZED-QUICKSORT의 실행 시간이 O(n lg n)임을 직관적으로 봤음. 재귀의 각 단계별로 RANDOMIZED-PARTITION를 하므로, 깊이가 Θ(lg n), 단계별로는 O(n) 만큼 걸리므로. 가장 불균형한 부분에 몇 단계 조금 추가해도 전체가 O(n lg n)임. 이걸 구체적으로 분석하려면 우선 분할 과정이 어떻게 작동하는지 이해하고, 예상 실행 시간의 상계 O(n lg n)를 도출하는 법을 이해하면 됨. 여기에 7.2 절에서 봤던 최고의 경우 Θ(n lg n)랑 결합하면 예상 실행 시간이 Θ(n lg n)임을 알 수 있음.
실행 시간과 비교
QUICKSORT와 RANDOMIZED-QUICKSORT의 차이점은 기준 원소 잡는 방법일 뿐. 그러므로 전자를 분석하면 후자도 손쉽게 분석할 수 있을 것.
QUICKSORT의 실행 시간은 사실상 PARTITION이 좌지우지. PARTITION 한 번 호출하면 O(1) + 3-6번 줄에 for문 돌아가는 거에 비례한 시간이 걸림. 이때 4번 줄이 몇 번 호출되는지를 세면 전체 시간 구할 수 있음.
보조정리 7.1
X가 크기가 n인 배열에 대한 QUICKSORT를 실행 할 때 4번 줄에서 실행된 모든 비교 횟수라 가정. 이때 QUICKSORT의 실행 시간은 O(n + X)
증명
PARTITION을 최대 n 번 호출하며, 각각 상수 시간의 일과 for문에 의해 몇 번 돌게 됨. 여기서 도는 줄은 4번 줄임.
결국 핵심은 X를 구하는 것. PARTITION의 각 호출별로 보지는 않을 것임. 분석을 쉽게 하기 위해 배열의 원소들을 각각 z1, …, zn로 표기. 이때 zi는 i번째로 작은 원소. 여기에 집합 Zij = {zi, zi + 1, …, zj}이 있다고 가정.
알고리듬이 zi와 zj를 비교할 때가 언제일까? 이걸 알려면 우선 각 짝마다 최대 한 번 비교된다는 점을 알면 됨. 어차피 원소는 오로지 기준과 비교하고, 해당 PARTITION 끝나면 어차피 기준은 앞으로 더 이상 비교 안 하니까.
다음과 같이 정의:

여기서 알고리듬 실행 중 단순히 PARTITION 호출하거나 한 반복 도중이 아니라, 아무 시간에 비교가 발생하는지 안하는지를 고려. 각 짝이 최대 한 번 비교되므로, 손쉽게 알고리듬이 다음과 같이 총 비교 횟수를 구할 수 있음:
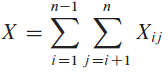
각 면의 기대값을 바탕으로 기대값의 선형성과 보조정리 5.1를 활용하여:
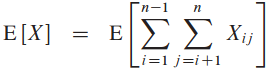
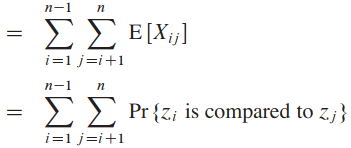
이제 Pr{zi를 zj와 비교}를 이제 계산해야함. 이때 우리가 하는 분석에서는 RANDOMIZED-PARTITION 과정이 각 기준을 무작위로, 독립적으로 고른다고 가정함.
두 아이템이 비교되지 않는 경우? 예를 들어 1에서 10 사이의 숫자로 구성된 입력을 가정. 기준이 7이라고하면 {1, 2, 3, 4, 5, 6}, {8, 9, 10} 둘로 분할 될 것. 이러면 기준 7은 모든 다른 원소들과는 비교되었겠지만, 앞의 집합은 뒤의 집합과 앞으로 비교될 일이 없음.
일반적으로 원소가 서로 다르다고 가정. zi < x < zj인 기준 x를 고를 경우 zi와 zj는 절대 서로 비교될 일이 없음. 반대로 zi를 기준으로 고를 경우 자기 빼고 나머지와 전부 비교 연산을 할 것. zj를 기준으로 골라도 마찬가지. 그러므로 zi와 zj는 둘 중 하나가 기준이어야만 서로 비교가 됨.
이제 이 마지막의 경우의 확률만 구하면 됨. 그럼 당연히 Zij의 원소의 개수는 j - i + 1개니까 1/(j - i + 1)임:
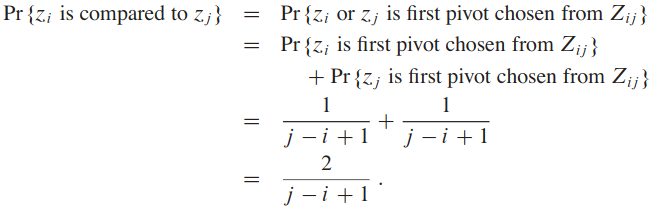
두번째 줄이 가능한 이유는 두 사건이 상호 배타적이기 때문. 위의 공식을 합치면:
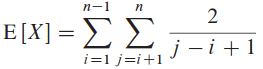
이제 변수를 다른 변수로 치환해주고, 조화 급수로 유계를 해주면 됨:
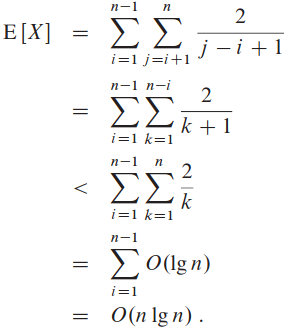
그러므로 값이 서로 다른 배열에 대해 RANDOMIZED-PARTITION사용 시 퀵 정렬의 실행 시간이 O(n lg n)임.
