2. 시작하기

2.1 삽입 정렬

삽입 정렬은 정렬 문제 sorting problem을 해결함.

• 입력: n 개의 순차적 숫자 <a1, a2, …, an>.
• 출력: 입력에 대해 a'1 ≤ a'2 ≤ … ≤ a'n을 만족하는 (재배열한) 순열 <a'1, a'2, …, a'n>.

정렬할 숫자들을 키 key라고 부름. 개념적으로는 연속체를 정렬하는 거긴 한데, 보통 n 개의 원소를 갖는 배열이 입력으로 옴.

이 책은 C/C++/Java/Python/Pascal과 비슷한 의사 코드 pseudocode로 알고리듬을 프로그램의 형태로 작성함.

삽입 정렬 insertion sort은 적은 수의 원소를 정렬할 땐 효율적임.

이 알고리듬은 입력 숫자들을 제자리에 in place 정렬함. 배열 내에서 재배열이 일어남. 이때 임의의 시간에 배열 외부에 최대 하나의 상수를 사용함.

삽입 정렬 (A)

for j = 2 to A.length
    key = A[j]
    // A[j]를 정렬된 연속체 A[1..j - 1]에 삽입
    i = j - 1
    while i > 0 and A[i] > key
    	A[i + 1] = A[i]
        i = i - 1
    A[i + 1] = key

삽입 정렬의 루프 불변성과 올바름

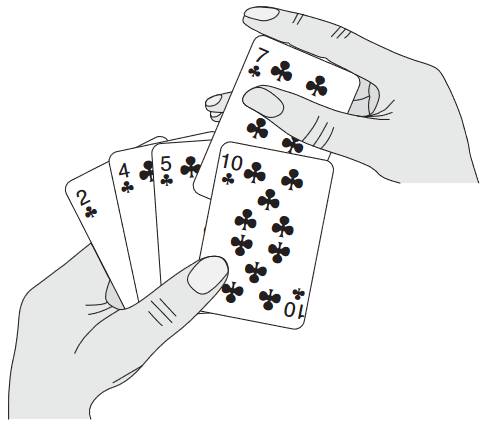
색인 j가 손에 넣을 "현재 카드"를 의미. for 루프의 각 반복의 시작마다 부분배열 A[1..j - 1]이 현재 손에 있는 정렬된 패를 의미. 나머지 부분배열 A[j + 1..n]이 아직 책상 위에 있는 카드 무더기. 사실 A[1..j - 1]의 원소들은 원래 위치가 1부터 j - 1 사이에 있던 애들이고, 정렬이 이제 되었을 뿐임. 이러한 A[1..j - 1]의 속성을 루프 불변성 loop invariant라 부름.

루프 불변성을 통해 이 알고리듬이 올바른지 이해할 수 있음. 루프 불변성에 대해 세 가지를 보여야 함:

• 초기화 initialization: 루프의 첫번째 반복 이전에 참이어야 함.
• 유지보수 maintenance: 각 루프 반복 이전에 참이어야 하고, 다음 반복 이전까지 참이어야 함.
• 종료 termination: 루프가 종료할 때 불변성을 통해 알고리듬이 올바름을 알 수 있는 유용한 속성을 제공함.

초기화랑 유지보수만 보장되어도 루프의 각 반복마다 루프는 불변함. 수학적 귀납법과 사고의 흐름이 유사함.

세번째 속성이 젤 중요함. 루프 불변성으로 루프가 올바르다는 것을 보이는 거니까. 보통 루프 불변성을 루프 종료 조건과 함께 사용함. 이게 귀납법과의 차이점인데, 귀납법은 무한대까지 가는 반면, 여기서는 루프가 종료될 때 "귀납"이 종료됨.

직접 보도록 확인해보자:

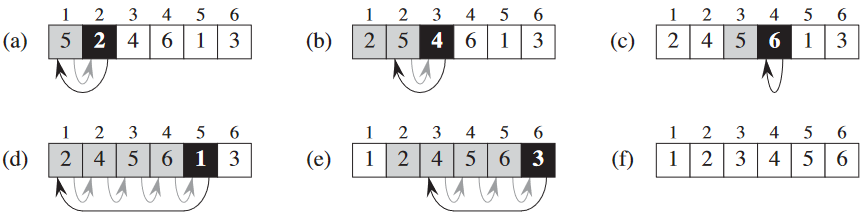
• 초기화: 첫번째 반복인 j = 21일 때 부분집합 A[1..j - 1]은 오로지 하나의 원소 A[1]로만 이뤄져 있으므로 원래 원소 A[1] 그 자체이며, 그 자체로도 자명하게 정렬되어있어 루프 불변성이 참임을 알 수 있음.
• 유지보수: for 루프의 각 본문이 A[j - 1], A[j - 2], A[j - 3]로 연속되는 원소들을 A[j]를 위한 올바른 위치가 나올 때까지 한 칸 씩 오른쪽으로 옮기고(줄 4-7), 빈 곳에 A[j] 넣음(줄 8). 부분열 A[1..j]는 원래 A[1..j]에 있던 애들 그대로 갖고 있음. 단지 정렬이 되었을 뿐.
  두번째 속성을 좀 더 엄밀히 보이려면 줄 5-7의 while문에서도 보여야하지만 굳이 그렇게까지 엄밀하게 하진 않았음.
• 종료: for 루프 종료 조건은 j > A.length = n임. 각 루프마다 j가 1만큼 증가하므로 이때 반드시 j = n + 1가 됨. n + 1를 j로 대체하게 되면 부분열 A[1..n]이 A[1..n]의 원래 원소를 가지면서도 정렬된 상태가 됨. 이때 A[1..n]가 전체 배열이므로 전체 배열이 정렬되었음을 알 수 있으므로, 알고리듬은 올바름.

의사코드 관례

• 인덴션이 곧 블록 구조를 의미. (파이썬 생각하면 됨)
• 반복문 while, for, repeat-until과 조건문 if-else은 C/C++/Java/Pascal/Pascal이랑 비슷하다 보면 됨. 이 책에서는 C++/Java/Pascal과는 다르게 루프 카운트가 루프 끝나도 값이 유지가 됨. for 루프가 루프 카운터를 각 반복마다 증가시킬 때 to라는 키워드 사용, 루프 카운터를 감소시킬 땐 downto 사용. 루프 카운터 값이 1보다 큰 값만큼 바뀌면 해당 값은 by 키워드 다음에 나옴.
• 기호 "//"는 주석임
• 다중 할당 i = j = e은 마치 j = e 이후 i = j와 같음.
• 변수는 주어진 절차에 지역적임. 따로 명시적으로 표기해주지 않는 이상 전역 변수는 없음.
• 배열의 원소를 배열 이름 + [ + 색인 + ]의 형태로, A[i]처럼 표기.
• 복합 자료를 속성 attribute으로 이루어진 오브젝트 object의 형태로 표현. 개체지향 프로그래밍 언어처럼 사용한다 생각하면 됨. A.length처럼. 포인터가 아무것도 안 가리킬 땐 NIL이라는 특수한 값 줌.
• 절차에 매개변수를 값에 의한 by value 전달을 함.
• 호출된 절차 내의 return문은 제어권을 바로 호출하는 절차로 돌려주면서 대부분의 경우 값을 반환해줌. 한 return문에 여러 가지를 반환해줄 수도 있음.
• 불리언 연산자 "and", "or" 등은 단락 회로임. 즉, "x" and "y"를 평가할 땐 "x"부터 평가함. "x"가 FALSE면 전체 표현식은 TRUE가 될 수 없으니 "y" 평가 안 함.
• error 키워드를 통해 절차가 호출될 때 어떤 조건이 잘못되었음을 알림. 호출한 절차가 이 오류를 처리해야하므로 따로 액션을 취하진 않음.

2.2 알고리듬 분석

알고리듬을 분석 analyze한다는 것은 알고리듬이 필요로하는 자원을 예측하는 것. 알고리듬 분석을 해서 어떤 알고리듬이 제일 효율적인지 판단 가능.

이 책에서는 기본적으로 임의 접근 기계 random-access machine (RAM)라는 프로세서 하나만 사용하는 것으로 가정.

엄밀히 말하면 RAM 모델에는 명령어가 무엇이 있는지, 그 비용이 얼마인지를 정의하기는 해야하는데, 솔직히 귀찮음. RAM 모델은 기본적으로 실제 컴퓨터들이 공통적으로 갖는 명령어들, 대표적으로 산술, 자료 옮기기, 제어 등 다 갖고 있음.

RAM의 자료형은 정수형이랑 소수형. 정밀도는 대부분의 경우 딱히 중요 X. 자료형의 크기는 워드와 동일. 입력의 크기가 n이면 보통 정수가 c log2 n 비트로 구성됨. c는 1 이상의 상수.

좀 애매한 부분도 있는데, 웬만하면 2의 제곱수 계산은 상수 시간 내에 된다고 가정할 것.

메모리 계층은 현대 컴퓨터와 유사하지 않음. 캐시나 가상 메모리 없음.

간단한 알고리듬 분석에도 여러 수학 이론 필요. 조합론, 확률론, 대수학 쪽 센스, 가장 중요한 부분을 공식화하는 능력 등.

삽입 정렬 분석

일반적으로 알고리듬에 걸리는 시간은 입력의 크기와 비례.

입력 크기 input size의 정의는 문제에 따라 다름. 대부분의 경우 입력의 원소의 개수임. 물론 비트의 총 개수 등도 가능함.

특정 입력에 대한 알고리듬의 실행 시간 running time은 가장 기본적인 연산, 혹은 "스텝"의 개수를 의미. 이때 각 i 번째 실행은 ci 상수 시간 걸린다고 가정.

각 n = A.length일 때, j = 2, 3, …, n마다 while 루프가 돈 개수를 tj라 둠.

코드	비용	횟수
for j = 2 to A.length	c1	n
key = A[j]	c2	n - 1
// A[j]를 정렬된 연속체 A[1..j - 1]에 삽입	0	n - 1
i = j - 1	c4	n - 1
while i > 0 and A[i] > key	c5	∑j=2ntj
A[i + 1] = A[i]	c6	∑j=2n(tj - 1)
i = i - 1	c7	∑j=2n(tj - 1)
A[i + 1] = key	c8	n - 1

T(n) = c1n + c2(n - 1) + c4(n - 1) + c5∑j=2ntj + c6∑j=2n(tj - 1) + c7∑j=2n(tj - 1) + c8(n - 1)

만약 최고의 경우, 즉 이미 정렬된 배열이 들어오면 tj = 1이므로

T(n) = c1n + c2(n - 1) + c4(n - 1) + c5(n - 1) + c8(n - 1)
= (c1 + c2 + c4 + c5 + c8)n - (c2 + c4 + c5 + c8)

즉, n에 대한 선형 함수 linear function임.

만약 배열이 전부 정렬된 순서와 정반대로 되어있다면, tj = j임.

∑j=2nj = ((n(n + 1)) / 2) - 1

그리고

∑j=2n(j - 1) = ((n(n - 1)) / 2)

그러므로 이건 최악이 경우가 됨.

T(n) = c1n + c2(n - 1) + c4(n - 1) + c5(((n(n + 1)) / 2) - 1) + c6((n(n - 1)) / 2) + c7((n(n - 1)) / 2) + c8(n - 1)
= (c5 / 2 + c6 / 2 + c7 / 2)n2 + (c1 + c2 + c4 + c5 / 2 - c6 / 2 - c7 / 2 + c8)n - (c2 + c4 + c5 + c8)

이건 n에 대한 이차 함수 quadratic function임.

최악의 경우와 평균의 경우

보통은 최악의 경우 실행 시간 worst-case running time에 좀 더 집중함. 즉, 크기 n인 모든 입력에 대해 나올 수 있는 가장 실행 시간이 긴 경우.

• 최악의 경우 실행 시간이 모든 입력에 대한 상한선을 정해줌.
• 몇몇 알고리듬에서는 최악의 경우가 자주 일어나기도 함.
• "평균의 경우"가 최악의 경우랑 비슷한 수준으로 성능이 안 좋음.

어떤 경우엔 평균의 경우 average-case 실행 시간에 집중할 때도 있음. 나중에 확률론적 분석 probabilistic analysis를 보게될 것. 물론 무엇이 평균인지가 문제임. 입력 크기가 고정되어있을 거라고 볼 수도 있음. 근데 실무에서는 보통 그러지 않으므로 무작위 알고리듬 randomized algorithm로 확률론적 분석을 하여 예상 expected 실행 시간 추정.

성장률

위에서 구한 성능 공식을 더 추상화한 것이 성장률 rate of growth 혹은 성장 순서 order of growth. 이제부터는 성능의 최고 차항만 고려. 삽입 정렬의 최악의 경우를 이제부터 Θ(n2)("세타 엔 제곱"이라 읽음)로 표기.

보통 한 알고리듬이 다른 알고리듬보다 최악의 경우 실행 시간이 더 낮은 성장률을 가질 때 더 효율적이라고 판단. 물론 입력 크기가 작으면 계수라든가의 요소 때문에 성장률이 더 낮아도 높은 게 더 효율적일 수 있는데, 충분히 큰 값에 대해서는 아님.

2.3 알고리듬 설계

여러 설계 기술이 있음. 삽입 정렬에서는 증가 incremental 접근법 사용. 부분열 A[1…j - 1] 정렬했으니A[j] 하나 추가해서 부분열 A[1…j]를 얻는 것

2.3.1 분할정복법

수많은 유용한 알고리듬은 구조적으로 재귀적 recursive임. 얘네는 보통 분할정복 divide-and-conquer 접근법을 사용. 문제를 여러 원본 문제와 유사한 형태의 크기가 더 작은 하위 문제로 분할해서 푸는 것. 얘네를 각각 풀고 합쳐서 또다시 하위 문제가 되고, 이게 원본 문제가 될 때까지 재귀적 반복.

• 분할 Divide: 문제를 더 작은 동일한 하위 문제로 분할
• 정복 Conquer: 하위 문제를 재귀적으로 해결.
• 결합 Combine: 원본 문제의 해답으로 하위 문제의 해답들을 결합.

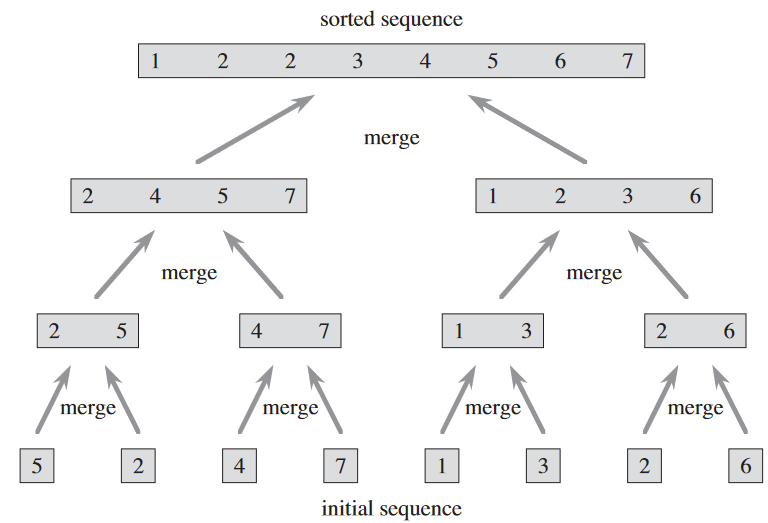
병합 정렬 merge sort이 분할정복의 전형적인 한 예.

• 분할: n 개 원소 연속체를 각각 n / 2 개의 원소를 갖는 부분연속체로 분할
• 정복: 병합 정렬로 두 부분연속체를 정렬
• 결합: 정렬된 두 부분연속체를 병합하여 정렬된 정답 겟.

연속체의 크기가 1일 때 재귀는 "바닥을 만남".

핵심은 두 정렬된 연속체가 "결합"되는 지점. 예비 절차 "MERGE(A, p, q, r)에서 배열 A와 p ≤ q < r를 만족하는 색인 p, q, r이 주어졌을 때 부분열 A[p..q]랑 A[q + 1..r]이 정렬되었다고 가정. 이때 이 둘을 병합 merge하여 하나의 정렬된 배열로 만들어 현재 부분열 A[p..r]를 교체.

MERGE는 Θ(n). 병합하는 원소의 총 개수 n = r - p + 1. 두 연속체의 최소값만 비교하니 각 기본 단계는 상수 시간 걸림. 최대 n 개의 기본 단계만큼 실행하니 병합은 Θ(n) 시간 걸림.

각 연속체의 맨 뒤에 계산의 편의성을 위한 특수 값을 갖는 센티넬 sentinel 카드를 넣음. 여기서 센티넬의 값은 ∞.

MERGE(A, p, q, r)

n_1 = q - p + 1
n_2 = r - q
새 배열 L[1..n_1 + 1], R[1..n_2 + 1] 겟
for i = 1 to n_1
	L[i] = A[p + i - 1]
for j = 1 to n_2
	R[j] = A[q + j]
L[n_1 + 1] = ∞
R[n_2 + 1] = ∞
i = 1
j = 1
for k = p to r
	if L[i] ≤ R[j]
    	A[k] = L[i]
        i = i + 1
    else A[k] = R[j]
    	j = j + 1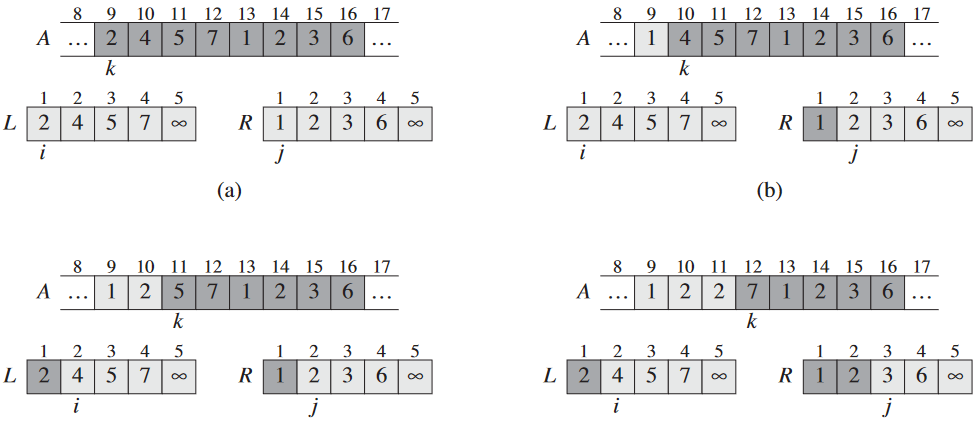

• 초기화: 루프 첫번째 실행 이전에 k = p이므로 부분열 A[p..k - 1]는 비어있음. 이 빈 부분열은 L과 R의 최소값 k - p = 0 개를 갖고 있음. i = j = 1이므로 L[i]과 R[j] 둘 다 각 배열의 최소값이며 아직 A에 복사되지 않음.
• 유지보수: L[i] ≤ R[j]라 가정. L[i]이 최소값이지만 아직 A에 복사 X. A[p..k - 1]가 k - p 개의 최소값 갖고 있으므로 14번 줄 이후 L[i]를 A[k]에 복사. A[p..k]는 k - p + 1개의 최소값 가짐. (for문에서) k를 증가하고 (15번 줄에서) i를 증가하면 다음 루프 불변성을 복구. L[i] ≥ R[j]라면 16-17번 줄이 루프 불변성을 유지하기 위한 작업함.
• 종료: 종료될 땐 k = r + 1. 부분열 A[p..k-1]는 A[p..r]이 됨. 얘는 L[1..n1 + 1]와 R[1..n2 + 1]의 k - p = r - p + 1 개의 최소값을 정렬된 순서로 가짐. L과 R은 둘이 합쳐 n1 + n2 + 2 = r - p + 3 개의 원소 가짐. 최대값 둘 빼곤 전부 A에 복사되었으며, 남은 둘은 센티넬임.

MERGE-SORT(A, p, r)

1	if p < r
2		q = ⌊(p + r) / 2⌋
3		MERGE-SORT(A, p, q)
4		MERGE-SORT(A, q+ 1, r)
5		MERGE(A, p, q, r)

크기가 1인 연속체 정렬하여 크기 2인 연속체 만들고, 이걸로 크기 4를 만들고...를 반복해서 크기 n / 2인 놈 합쳐서 n이 됨.

2.3.2 분할정복법 알고리듬 분석

알고리듬에 재귀 호출이 있다면 실행 시간을 점화식 recurrence equation 혹은 점화 recurrence로 표현 가능.

분할정복법의 점화 관계는 기본 패러다임의 세 가지 단계로 구분 가능. T(n)이 크기 n에 대한 문제의 실행 시간이라 가정. 문제의 크기가 충분히 작다(임의의 상수 c에 대해 n ≤ c)고 가정. 그러면 보통 Θ(1) 상수 시간에 해결. 문제 분할하면 a 개의 원본보다 1 / b 배 작은 하위 문제로 나뉜다고 가정. (병합정렬에서 a랑 b 둘다 2) 즉 총 aT(n / b) 시간 걸림. 하위 문제로 분할하는데 D(n) 시간 걸리고 해법 결합하는 데 C(n) 시간 걸린다고 가정.

T(n) =

• Θ(1) (n ≤ c인 경우)
• aT(n / b) + D(n) + C(n) (나머지 경우)

병합 정렬 분석

원본 문제 크기 2의 제곱수라 가정. 그러면 각 분할 단계마다 부분연속체의 크기가 정확히 n / 2으로 됨.

T(n)을 점화식으로 구해야 n 개의 숫자에 대한 병합 정렬의 최악의 경우 실행 시간을 구할 수 있음. 원소 하나면 상수 시간이고, 두 개 이상이면 다음과 같이 구분하여 분석 가능:

• 분할: 부분열의 중간만 구하는 거니까 상수 시간. D(n) = Θ(1).
• 정복: 두 하위문제를 재귀적으로 해결. 크기는 각 n / 2이므로 실행 시간 2T(n / 2)
• 결합: n 개의 원소를 갖는 부분열에 대한 MERGE 절차는 Θ(n) 시간 걸리므로 C(n) = Θ(n).

T(n) =

• Θ(1) (n = 1인 경우)
• 2T(n / 2) + Θ(n) (n > 1인 경우)

결국 T(n) = n log2 n. 점화식을 수학적으로 좀 더 표기하면 크기가 1인 문제를 해결할 때 걸리는 시간을 상수 c로 표현하면:

T(n) =

• c (n = 1인 경우)
• 2T(n / 2) + cn (n > 1인 경우)

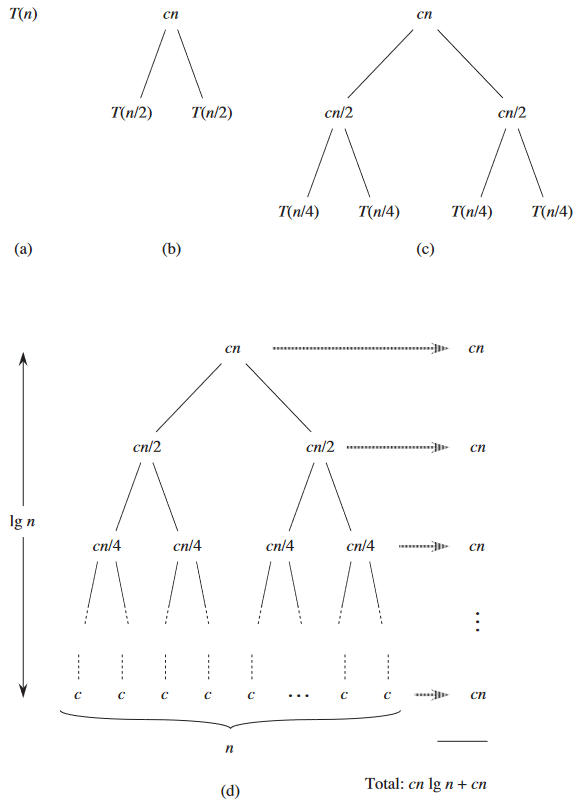
위의 그림에서 (a)가 T(n). (b)랑 (c)는 이 점화식의 확장. (d)가 최종적으로 얻을 수 있는 재귀 트리 recursion tree.