3. 함수의 성장
알고리듬의 실행 시간 성장률을 통해 알고리듬의 효율성을 간단하게 알 수 있고 다른 알고리듬과 비교해 상대적으로 성능을 비교할 수 있음. 입력 크기가 충분히 크면 실제 시간보다는 성장률로 대충 비교 가능.
이처럼 실행 시간 성장률이 의미가 있는 수준의 충분히 큰 입력 크기를 갖고 논하는 게 알고리듬의 점근적 asymptotic 효율성임. 즉, 유계 내의 입력 크기가 증가할 때 알고리듬의 실행 시간이 어떻게 증가하느냐임.
3.1. 점근 표기법
알고리듬의 점근적 실행 시간을 표기하는 방법은 0을 포함한 자연수의 집합에서 논함. 근데 이걸 실수나 자연수의 부분집합으로 변형하는 오용을 하기도 함.
점근 표기법, 함수, 실행 시간
점근 표기법은 함수에 적용.
우리가 적용할 함수들은 보통 알고리듬의 실행 시간을 의미. 근데 다른 의미(사용하는 공간 등)를 가질 수도 있음.
알고리듬의 실행 시간에 점근 표기법을 사용하더라도 어떤 실행 시간은 의미하는지 이해해야 함. 최악의 경우 실행 시간인지, 입력 크기와 무관한 실행 시간인지 등.
Θ 표기법
함수 g(n)가 주어졌을 때 Θ(g(n))이 함수들의 집합이라 부름.
Θ(g(n)) = {f(n) : n ≥ n0를 만족하는 모든 n에 대해 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n)를 만족하는 양수인 상수 c1, c2, n0이 존재 }
만약 충분히 큰 n 값에 대해 위와 같은 "샌드위치" 조건을 만족하는 상수 c1, c2가 존재한다면 f(n)은 Θ(g(n))의 원소임. ∈ 기호를 쓸 수도 있었지만 여기서는 f(n) = Θ(g(n))라 표기.
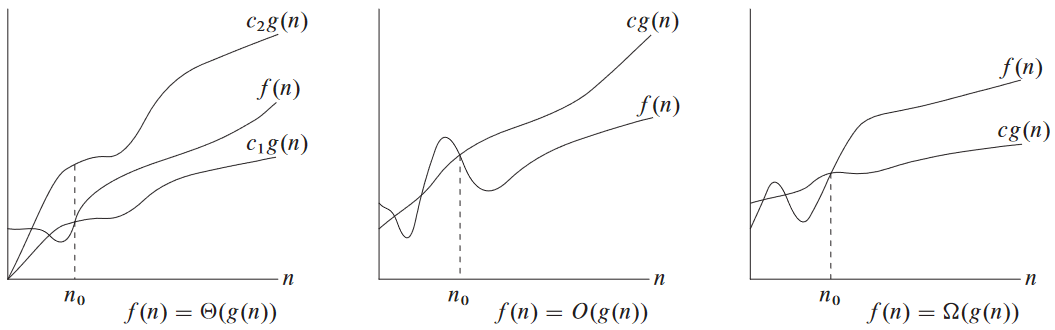
n0 이상인 모든 n에 대해서 f(n)의 값은 c1g(n) 이상, c2g(n) 이하의 상태. 즉, 상수 계수로 f(n)은 g(n)과 동일. 이때 g(n)을 f(n)의 점근적으로 좁은 유계 asymptotically tight bound라 함.
f(n) ∈ Θ(g(n))를 만족하는 모든 f(n)은 점근적 비음(非陰) asymptotically nonnegative임. 즉, n이 충분히 클 때 f(n)은 음수가 아니라는 뜻(점근적 양 asymptotically positive는 n이 충분히 클 때 양수라는 뜻). 그러므로 g(n)도 마찬가지로 점근적 비음이어야 함.
상수는 차수가 0인 다항식이므로 임의의 상수 함수를 Θ(n0) 혹은 Θ(1)로 표현.
O 표기법
Θ 표기법은 점근 상하한이 존재. 오로지 점근 상한 asymptotic upper bound만 존재할 때 O 표기법 사용.
O(g(n)) = {f(n) : n ≥ n0를 만족하는 모든 n에 대해 0 ≤ f(n) ≤ cg(n)를 만족하는 양수인 상수 c, n0이 존재 }

f(n) = Θ(g(n))이면 f(n) = O(g(n))임.
이때 기울기가 양수인 임의의 선형 함수는 O(n2)임. 이건 단순 상한의 개념이기 때문이고, Θ는 좁은 한계이기 때문.
O 표기법을 사용하면 알고리듬의 실행 시간을 대충 구조만 보고 검사할 수 있음. 삽입 정렬 알고리듬은 이중 루프를 가지므로 대충 최악의 경우 O(n2)이라 하는 것.
O 표기법은 상한을 의미하기에 모든 입력에 대한 알고리듬의 실행 시간에 대한 한계점을 갖는 것. Θ는 삽입 정렬의 최악의 실행 시간을 한계로 갖긴 하지만 그게 모든 입력에 대해 그러한 한계를 갖지는 않음.
그래서 보통 O(n2)라고 하면 최악의 경우 실행 시간이 O(n2)라는 뜻.
Ω 표기법
O 표기법이 점근 상한이라면 Ω 표기법("빅 오메가" 혹은 "오메가"라 부름)은 점근 하한 asymptotic lower bound를 의미.
Ω(g(n)) = {f(n) : n ≥ n0를 만족하는 모든 n에 대해 0 ≤ cg(n) ≤ f(n)를 만족하는 양수인 상수 c, n0이 존재 }

다음 정리를 얻을 수 있음:
Theorem 3.1
임의의 두 함수 f(n), g(n)에 대해 f(n) = Θ(g(n)) ⇔ f(n) = O(g(n)) 그리고 f(n) = Ω(g(n))이다.
알고리듬의 실행 시간이 Ω(g(n))이란 뜻은 그 어떠한 값이 입력 크기로 정해지더라도 충분히 큰 n에 대해 최소한 g(n)의 상수 배율이라는 것.
그러므로 삽입 정렬의 실행시간은 Ω(n)이면서 O(n2). 물론 삽입 정렬의 최악의 경우 실행 시간을 Ω(n2)이라 할 수도 있다. 실제로 그러한 입력이 존재할 수도 있으니까.
방정식과 부등식에서 점근 표기법
공식에 점근 표기법이 등장하면 그건 그냥 임의의 함수 취급하겠다는 것. 즉, 2n2 + 3n + 1 = 2n2 + Θ(n)는 2n2 + 3n + 1 = 2n2 + f(n)랑 똑같이 보겠다는 것.
이걸 사용하면 2단원에서 병합 정렬의 최악의 경우 실행 시간 점화식을 다음과 같이 작성 가능:
T(n) = 2T(n / 2) + Θ(n)
표현식 안의 임의의 함수의 개수는 점근 표기법의 등장 횟수랑 같음. 즉,
∑i=1nO(i)
위에는 오로지 하나의 임의의 함수(i에 대한 함수)가 존재. 그러므로 이건 O(1) + O(2) + … + O(n - 1)와 다름.
만약 좌우항에 동시에 점근 표기법이 등장한다면, 마치 2n2 + Θ(n) = Θ(n2)처럼: 좌항에 그 어떤 임의의 함수가 있든지 간에 이 공식을 참으로 만드는 우항에 있는 임의의 함수를 정하는 방법은 반드시 존재함. 즉, 임의의 n에 대해 임의의 함수 f(n) ∈ Θ(n) 중에 2n2 + f(n) = g(n)를 만족하는 어떤 g(n)∈ Θ(n2)이 존재함. 방정식의 우항이 좌항보다 더 높은 위상의 디테일을 제공함.
이걸 활용하면
2n2 + 3n + 1 = 2n2 + Θ(n)
= Θ(n2)
o 표기법
O 표기법으로 주어진 상한은 점근적으로 좁지 않을 수도 있음. o 표기법으로 좁은 상한을 표현하도록 함. o(g(n)) ("리틀 오"라 부름)을 다음의 집합으로 정의.
o(g(n)) = {f(n) : n ≥ n0를 만족하는 모든 n에 대해 0 ≤ f(n) < cg(n)를 만족하는 양수인 상수 c, n0이 존재 }
O 표기법이랑 정의가 비슷해보이지만 f(n) = O(g(n))은 어떤 상수 c > 0에 대해 범위가 0 ≤ f(n) ≤ cg(n), f(n) = o(g(n))은 모든 상수 c > 0에 대해 범위가 0 ≤ f(n) < cg(n). 즉, o 표기법에서 함수 f(n)이 n이 무한대로 갈 때 g(n)와 상당히 가까운 관계가 됨.
limn→∞ f(n) / g(n) = 0
이라는 뜻.
ω 표기법
o 표기법과 마찬가지로 점근적으로 좁은 하한을 의미. ω(g(n)) ("리틀 오메가"라 읽음)은 다음의 집합으로 정의.
ω(g(n)) = {f(n) : n ≥ n0를 만족하는 모든 n에 대해 0 ≤ cg(n) < f(n)를 만족하는 양수인 상수 c, n0이 존재 }
한계가 존재한다면
limn→∞ f(n) / g(n) = ∞
가 됨을 내포하기도.
함수 비교
- 이행성 Transitivity:
- f(n) = Θ(g(n)) 그리고 g(n) = Θ(h(n))일 경우 f(n) = Θ(h(n))
- f(n) = O(g(n)) 그리고 g(n) = O(h(n))일 경우 f(n) = O(h(n))
- f(n) = Ω(g(n)) 그리고 g(n) = Ω(h(n))일 경우 f(n) = Ω(h(n))
- f(n) = o(g(n)) 그리고 g(n) = o(h(n))일 경우 f(n) = o(h(n))
- f(n) = ω(g(n)) 그리고 g(n) = ω(h(n))일 경우 f(n) = ω(h(n))
- 재귀성 Reflexivity:
* f(n) = Θ(f(n))- f(n) = O(f(n))
- f(n) = Ω(f(n))
- 대칭성 Symmetry:
* f(n) = Θ(g(n)) ⇔ g(n) = Θ(f(n)) - 전이 대칭성 Transpose Symmetry:
* f(n) = O(g(n)) ⇔ g(n) = Ω(f(n))- f(n) = o(g(n)) ⇔ g(n) = ω(f(n))
이걸 두 실수 a와 b 간의 비교와 비유해서 이해 가능.
- f(n) = O(g(n))은 곧 a ≤ b
- f(n) = Ω(g(n))은 곧 a ≥ b
- f(n) = Θ(g(n))은 곧 a = b
- f(n) = o(g(n))은 곧 a < b
- f(n) = ω(g(n))은 곧 a > b
f(n) = o(g(n))일 때 f(n)이 g(n)보다 점근적으로 작다 asymptotically smaller고 하고, f(n) = ω(g(n))일 땐 점근적으로 크다 asymptotically larger고 함.
- 삼분법 Trichotomy: 임의의 두 실수 a, b에 대해 다음 중 한 가지는 반드시 참임: a < b, a = b, a > b
모든 실수는 서로 비교 가능한데 모든 함수들이 점근적으로 비교 가능하진 않음. 두 함수 f(n)과 g(n)에 대해 f(n) = O(g(n))랑 f(n) = Ω(g(n)) 둘 다 참이 아닐 수도 있음.
3.2. 표준 표기법과 공통 함수
단조성
- 단조 증가 monotonically increasing
- 단조 감소 monotonically decreasing
- 강증가 strictly increasing
- 강감소 strictly decreasing
바닥과 천장
생략
모듈러 산술
생략
용어:
- 나머지 remainder (혹은 잔여물 residue)
- 동치 equivalent
다항식
생략
용어:
- 차수 d를 갖는 *n*에 대한 다항식 polynomial in n of degree d
- 계수 coefficient
- 다항식 유계 polynomially bounded
- 어떤 상수 k에 대해 f(n) = O(nk)일 때 f(n)은 다항식 유계가 존재함
지수
생략
로그
생략
용어:
- 다항로그식 유계 polylogarithmically bounded
- 어떤 상수 k에 대해 f(n) = O(logk n)일 때 f(n)은 다항로그식 유계가 존재함
팩토리얼
생략
용어:
- 스털링 근사 Stirling's approximation
- n! = √2π(n/e)n(1 + Θ(1/n))
함수 반복
초기 값 n에 대해 함수 f(n)을 i 번 반복 적용하는 것을 f(i)(n)으로 표기.
반복 로그 함수
log* n ("로그 스타"로 읽음)이 반복 로그. f(n) = log n일 때 log(i)n이 있다고 가정. 로그의 성질 상 log(i - 1)n > 0여야만 log(i)n가 정의됨.
log* n = min {i ≥ 0 : log(i - 1)n ≤ 1 }
위가 반복 로그 함수의 정의.
반복 로그 함수는 매우 느리게 증가하는 함수:
- log* 2 = 1
- log* 4 = 2
- log* 16 = 3
- log* 65536 = 4
- log* (265536) = 5
피보나치 수
생략.
용어:
- 피보나치 수 Fibonacci numbers
- 황금율 Φ
- 얘랑 얘의 짝 Φ^이 방정식 x2 = x + 1의 두 해.
