[밑바닥부터 시작하는 비트코인] 1. 유한체

alg0r1thm·2022년 4월 26일

블록체인

밑바닥부터 시작하는 비트코인

목록 보기

1/4

유한체에 대한 내용을 읽기 전에 모듈러 연산 을 읽고오면 도움이 될 것이다.

1.1 유한체의 필요성

이번 장은 타원곡선 암호를 파악하기 위해 필요한 유한체를 공부한다.
타원곡선 암호는 비트코인의 핵심인 전자서명과 서명 검증 알고리즘을 이해하는 데에 필수적이기 때문이다.
이를 통하여 슈노어 서명, 기밀 트랜잭션 및 첨단 비트코인 기술에 대해 좀 더 쉽게 접근할 수 있다.

1.2 유한체의 정의

우선 유한체의 각각의 성질은 아래와 같다.
- 유한성 ( finiteness ) : 원소의 개수가 유한
- 폐쇄성 ( closure ) : 연산의 결과도 동일 집합의 원소
- 결합성 ( associativity ) : $a + (b + c) = (a+b) +c$ , $a × (b× c) = (a× b)× c$
- 교환성 ( community ) : $a + b =b+a$ , $a× b=b× a$
- 분산성 ( distribution ) : $a× (b+c)=a× b+a× c$
- 항등원 ( identity ) 존재 : 각 요소 $a$ 에 대해 덧셈 항등원과 곱셈 항등원 존재
- 역원 ( inverse ) 존재 : 각 요소 $a$ 에 대해 덧셈과 곱셈 역원 존재. 단, 덧셈 항등원에 대한 곱셈 역원은 존재하지 않는다.

수학에서의 유한체는 아래 성질을 만족하는 2개의 연산자 ( + , × ) 를 가진 집합이다.
- 여기서 체(Field) 란 원소들 간의 덧셈,곱셈의 연산 결과가 다시 그 안에 있는 닫힘성을 갖는 대수적 구조를 말한다.
  - *원소들이 집합을 이룰때, 덧셈과 곱셈 연산을 자유롭게 사용할 수 있다. ( 2개 연산자 사용 )*
  - *집합의 각 원소가 0이 아닌 원소로 나눌 수 있는 대수적 구조이다. ( 곱셈 역원 존재 )*
  - 즉, 0으로 나누는 것을 제외하고는, 사칙연산을 비교적 자유롭게 사용 가능한 대수적 구조이다.
이는 집합의 원소 수가 유한하다는 특징을 가진다.

$a$ 와 $b$ 가 집합에 속해있으면, $a$ + $b$ 와 $a$ × $b$ 도 집합 안에 있다. ( 집합 위에 두 연산 +, ×가 닫혀 있음. )
집합에 0으로 표기하는 원소가 존재하고, 집합 내 다른 원소 $a$ 와 + 연산 결과는 $a$ 다. ( + 연산에 대한 항등원 존재)
집합에 1로 표기하는 원소가 존재하고 집합 내 다른 원소 $a$ 와 × 연산 결과는 $a$ 다. ( + 연산에 대한 항등원 존재 )
집합의 원소 $a$ 와 + 연산 결과가 0이 되게 하는 원소 b가 역시 집합에 속해있고 이러한 $b$ 를 -a로 표기한다. ( + 연산에 대한 $a$ 의 역원 $-a$ 존재)
0이 아닌 집합의 원소 $a$ 에 대해 $a$ × $b$ = 1 이 되게 하는 원소 $b$ 가 역시 집합에 속해 있고 이러한 $b$ 를 $a^{-1}$ 로 표기한다 ( × 연산에 대한 $a$ 의 역원 $a^{-1}$ 존재 )

각각의 성질을 풀어보면,
- 1번 성질
  - 덧셈과 곱셈에 대하여 닫혀있다.
  - 덧셈과 곱셈의 연산 결과가 집합 안에 있도록 두 연산을 정의해야한다.
  - 원소가 { 0, 1, 2 } 인 집합이 있다고 가정 할 때, 덧셈에 대해 닫혀있지 않다.
    - 1 + 2 = 3 이고, 3은 집합 안에 없기 때문이다.
    - 2 + 2 = 4 인 경우에도 4는 집합 안에 없기 때문이다.
  - 반면 원소가 { 1, 0, -1 } 인 집합이 있다고 가정 할 때, 일반 곱셈에 대해 닫혀있다.
    - 임의의 2개 원소의 곱셈 결과가 항상 집합 안에 존재하기 때문이다.
  - 수학에서는 위 2개의 집합이 모두 곱셈에 대하여 닫혀있도록 정의 가능하다.
  - 하지만 여기서 알아야할 중요한 개념은 다른 방식으로 곱셈과 덧셈이 정의 가능하다는 점이다.
- 2번과 3번 성질
  - 덧셈과 곱셈에 대한 항등원이 집합 내에 있다는 개념이다.
  - 이들은 각각 집합에서의 0 과 1 을 의미한다.
- 4번 성질
  - 덧셈에 대한 역원이 집합 내에 있다는 뜻이다.
  - 집합 내에 $a$ 가 존재 할 때 $-a$ 또한 집합 내에 존재한다는 뜻이다.
  - 이는 덧셈에 대한 역원을 사용하여 뺄셈 또한 정의가 가능하다는 것을 의미한다.
- 5번 성질
  - 곱셈에 대하여 4번과 똑같은 성질을 지닌다는 것을 의미한다.
  - $a$ 가 집합 내에 존재할 때, $a^{-1}$ 또한 집합 내에 존재할 수 있다는 것을 의미한다.
  - 즉 $a$ × $a^{-1}$ = 1 이다.
  - 이는 곱셈에 대한 역원을 사용하여 나눗셈 또한 정의가 가능하다는 것을 의미한다.
  - 하지만 유한체 내에서 나눗셈을 정의하는 것이 가장 까다롭다.
  - 그림1 에 대한 부연설명
    - 덧셈 연산에서 1+2 를 예시를 모듈러 연산을 통해 설명하면 아래와 같다.
      $(1+2)\ mod\ 3 = 0$
  - 유한 개수의 숫자를 원소로 하는 집합이 있을 때, 해당 집합의 원소 개수는 유한하다.
  - 따라서 집합의 크기를 표현하는 어떠한 값을 정할 수 있는데 이를 집합의 위수 라고 한다.
  - 집합의 위수는 값 $p$ 로 표현한다.

닫혀있다는 의미에 대하여..

위에 나와있는 설명중 닫혀있다는 뜻이 이해가 가지 않을 수 있다.
그 이전에 왜 유한체에서 소수만을 사용하는지 먼저 설명하고 넘어가겠다.
예시를 위해 위수 $p$ 가 $7$ 인 경우를 생각해보자.
$F_{7}=\{\ 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6\ \}$ 일 때, 대수적 구조에 의해 사칙연산에 대하여 닫혀있다고 말한다.
간단하게 말하면 사칙연산에 대한 값을 해당 집합이 포함하고 있는 구조라는 것을 의미한다.
즉, 연산을 통해 나온 값이 해당 집합의 원소여야 한다는 뜻이다.
이런 경우를 해당 연산에 대하여 닫혀있다고 표현한다.

요약
집합 $A$ 에 속하는 원소 $a$ 와 $b$ 를 대상으로 연산을 진행할 때, 결과 역시 $A$ 에 속해 있는 경우.

1.3 유한집합의 정의

유한체 집합의 위수가 $p$ 일때, 집합의 원소는 0, 1, 2, ... $p$ -1 로 정의할 수 있다.
굳이 일반적인 0 과 자연수 값을 가지는 집합의 원소로 생각할 필요는 없다.
일반 숫자의 성질도 지니지만 덧셈, 뺄셈, 곱셈 방법에 있어 차이가 있다.
일반적으로 유한체의 집합은 다음과 같이 표기한다.

F_p = \{\ 0,\ 1,\ 2,\ ...\ ,\ p-1\ \}

이 때 중괄호 안에 있는 것은 집합의 원소이며 $F_p$ 는 위수 $p$ 의 유한체라고 읽는 특정 유한체이다.
- $*F_p$ 에서 $p$ 는 집합의 위수로 집합 안의 원소 개수를 의미한다.*
중괄호 사이의 0, 1, 2 등으로 표기한 숫자들은 유한체 내에서의 서로 다른 원소를 의미한다.
예시로 위수 7의 유한체는 다음과 같이 표기할 수 있다.

F_{7} = \{\ 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6\ \}

유한체의 위수는 항상 가장 큰 숫자 원소보다 하나가 더 많은 것을 볼 수 있다.
또한 유한체는 위수가 소수로 표기되는데, 유한체는 반드시 소수이거나 소수의 거듭제곱을 위수로 가져야 한다.
소수가 아닌 경우에는 각각 연산에 대한 역원이 존재하지 않는 경우가 있기 때문에 유한체의 성질에 위배되기 때문이다.

1.4 파이썬을 통한 유한체 구현

파이썬을 통해 유한체의 원소를 표한하는 코드를 작성해보자.
jupyter notebook 을 실행 후 code-ch01/Chapter1.ipynb 를 통하여 결과값을 볼 수도 있다.

class FieldElement:
    
    def __init__ (self, num, prime):
        if num >= prime or num <0: #1
            error = 'Num {} not in field range 0 to {}'.format(
                num, prime -1
            )
            raise ValueError(error)
        self.num = num #2
        self.prime = prime
        
    def __repr__(self):
        return 'FieldElement_{}({})'.format(self.prime, self.num)
    
    def __eq__(self, other):
        if other is None:
            return False
        return self.num == other.num and self.prime == other.prime #3

각각 주석 처리 된 부분을 단계별로 풀어서 이해해보자.
1. num과 prime을 인수로 받은 후 num의 경곗값을 포함해 0 과 prime - 1 의 사이값인지 조사한다.
  아닌 경우에는 FieldElement가 유효하지 않은 값이므로 ValueError를 반환한다.
  ( 이 때, ValueError 는 부적절한 값을 얻을 시 발생하는 오류이다. )
2. init 메소드의 나머지 부분에서 조사된 인수 값으로 객체를 초기화 한다.
3. eq 메소드는 FieldElement Class 의 두 개체가 같은지 검사한다.
  ( num과 prime 속성이 같은 경우 True 를 반환한다. )
실행 시 아래와 같은 값을 볼 수 있을 것이다.

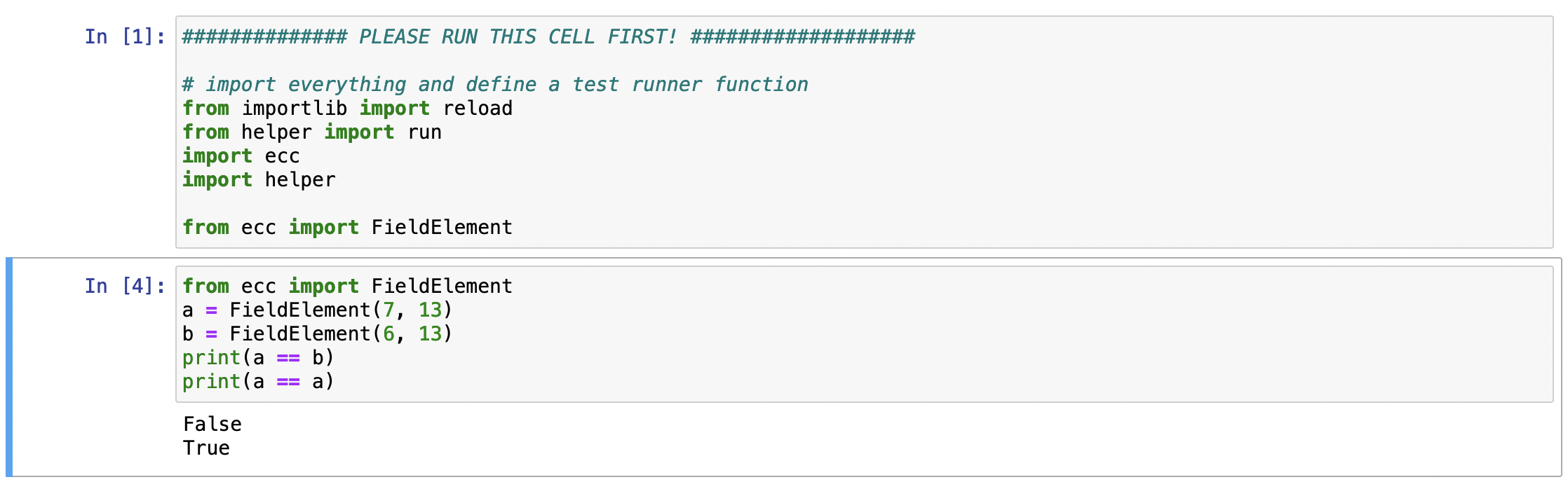
1.5 파이썬을 통한 나머지 연산 구현

이번 문단을 통해 덧셈, 뺄셈, 곱셈, 나눗셈 연산에 대해 닫힌 유한체를 구현해보자.
간단한 예시를 통해 간단히 되짚어보고 넘어가보자.

현재 시간이 3시라면, 지금으로부터 47시간 후는 몇시가 될까?

일반적인 계산식으로 해당 시간을 구하면 아래와 같이 표현 할 수 있다.

(\ 3+47\ )\ \%\ 12=2

수식으로만 보았을 때 잘 이해가 가질 않는다면 아래 그림을 보고 다시 이해해보자.

12시간이 지날 때 마다 원을 한바퀴씩 돌게되고, 처음 시작할 때의 위치로 돌아가는 모습을 볼 수 있다.
음수에 대해서도 마찬가지로 연산을 동일하게 수행할 수 있다.

현재 시간이 3시라면, 지금으로부터 16시간 전은 몇 시일까?

위와 마찬가지로 간단한 수식을 통해 시간을 구할 수 있다.

(\ 3-16\ )\ \%\ 12=11

그럼 현 시간이 12분이라면, 지금으로부터 350분 이후는 몇 분일까?

분이라고 해도 문제 될 것 없이 배웠던 대로 수식을 작성해보자.

(\ 12+350\ )\ \%\ 60=15

시 와는 다르게 분은 60분이 기준이 되므로 60으로 나머지 연산을 수행하여 값을 구할 수 있다.
그럼 파이썬을 통해 나머지 연산을 수행해보자.

>>> print( 7 % 3 )
1

>>> print( -27 % 13 )
12

1.6 유한체 덧셈과 뺄셈

그럼 위 개념을 바탕으로 유한체의 덧셈과 뺄셈을 정의해보자.
유한체에서는 덧셈을 정의할 때 결과가 유한체 내에 속해 있도록 해야한다.
이는 덧셈에 대하여 수학적으로 닫혀있어야함을 의미한다.

1.6.1 유한체 덧셈의 개념

우선 19를 위수로 하는 유한체가 있다고 가정해보자.

F_{19}=\{\ 0,\ 1,\ 2,\ ...\ 18\ \}

집합론에 의해 $a$ , $b$ ∈ $F_{19}$ 가 되며 $**a$ , $b$ 는 $F_{19}$ 의 원소**이다.
수학적으로 덧셈에 대해 닫혀있어야 한다는 뜻은 아래와 같다.

a\ +\ _{f}b \in\ F_{19}

일반 정수에서의 덧셈과 구별하기 위해 $+$ 가 아닌 $+_{f}$ 로 구분하여 유한체 연산임을 표시했다.

1.6.2 유한체 덧셈의 이해

이러한 식은 나머지 연산을 사용하면 항상 만족하며, $a+_{f}b$ 를 다음과 같이 정의할 수 있다.

a\ +_{f}b=(\ a\ +\ b\ )\ \%\ 19

간단한 수식을 통해 예를 들어보면 아래와 같이 표현할 수 있다.

7\ +_{f}8=(\ a\ +\ b\ )\ \%\ 19 =15\\11\ +_{f}17=(\ 11\ +\ 17\ )\ \%\ 19=9

결국 임의의 수 2개를 꺼내 더한다음 그 수를 위수로 나눈 나머지를 구하면 된다.

1.6.3 유한체 덧셈의 일반형 정의

결과적으로 이를 일반화 하면 아래와 같은 수식으로 표현 가능하다.

a\ +_{f}b=(\ a+b\ )\ \%\ p \\이\ 때,\ p는\ 위수이다.

1.6.4 역원을 통한 뺄셈의 이해

덧셈에 대한 역원 또한 아래와 같이 정의 가능하다.

-_{f}a=(\ -a\ )\ \%\ p

간단한 수식을 통해 예를 들어보면 아래와 같이 표현할 수 있다.

-_{f}9=(\ -9\ )\ \%\ 19\ =10

여기서\ -_{f}9(\ =10\ )\ 은\ 9의\ 역원이므로,\\9+_{f}10=0\ 으로\ 표현\ 가능하다.

이를 통해 10은 9의 덧셈에 대한 역원임을 알 수 있다.

1.6.5 역원을 통한 뺄셈의 정의

그럼 이 방식을 통해 유한체에서도 동일하게 뺄셈에 대하여 정의가 가능하다.

a-_{f}b=(\ a-b\ )\ \%\ p \\\Rightarrow\ a,\ b\ \in\ F_{p}

간단한 수식을 통해 예를 들어보면 아래와 같이 표현할 수 있다.

11-_{f}9=(\ 11-9\ )\ \%\ 19=2 \\ 6-{f}13=(\ 6-13\ )\ \%\ 19=12

1.7 파이썬을 통한 유한체 덧셈과 뺄셈 구현

앞서 작성했던 유한체 코드 내에서 새로운 메소드를 정의 가능하다.
add 와 sub 메소드로 아래와 같이 명령을 실행 가능하다.

>>> from ecc import FieldElement
>>> a = FieldElement(7,13)
>>> b = FieldElement(12,13)
>>> c = FieldElement(6,13)

>>> print(a+b==c)
True

그럼 우선 덧셈을 정의하는 add 메소드를 구현해보자.
나머지 연산을 활용하여 아래와 같은 새 메소드를 FieldElement 에 아래와 같이 작성 가능하다.

class FieldElement:
...
						def __add__(self, other): #1
							if self.prime != other.prime:
								raise TypeErroe('Cannot add two numbers in differnet Fields')
							num = (self.num + other.num) % self.prime #2
							return self.__class__(num, self.prime) #3

각각 주석 처리 된 부분을 단계별로 풀어서 이해해보자.
1. 더해지는 수와 더하는 수의 위수가 동일한지 검증한다. 위수가 다르면 계산의 의미가 없기 때문이다.
2. 나머지 연산을 활용하여 유한체 덧셈을 정의한다.
3. FieldElement Class ( 자기 자신 클래스 ) 의 인스턴스를 반환하여 self.class 로 쉽게 접근 할 수 있게 한다. 인스턴스를 생성하기 위하여 num과 self.prime 으로 정의된 2개의 인수를 클래스 생성자에게 넘기고 내부적으로 init 메소드가 앞서 정의된 인수를 통해 초기화한 인스턴스를 반환한다.

       class FieldElement:
       ...
       	def __sub__(self, other):
       		if self.prime != other.prime:						
       			raise TypeError('Cannot subtract two numbers in different Fields')
       		num = (self.num - other.num) % self.prime
       		return self.__class_(num, self.prime)

1.8 유한체 곱셈과 거듭제곱

유한체에서의 덧셈과 동일하게 곱셈도 닫혀있게 정의 가능하다.
나머지 연산을 이용하여 곱셈과 거듭제곱을 정의해보자.

1.8.1 유한체 곱셉 이해

우선 익숙한 정수집합에서의 곱셈의 기본 개념은 ‘여러 번 더하기’ 이다.

5\ \times\ 3 = 5+5+5=15

유한체에서의 곱셈도 비슷하게 정의 가능하다.
위수 $p$ 가 19인 유한체 $F_{19}$ 를 예시로 들면 아래와 같이 표현 가능하다.

5\ \times_{f}3=5+_{f}5+_{f}5

그럼 앞에서 배운 덧셈과 비슷하게 이 식을 풀어 나간다면 아래와 같다.

5\ \times_{f}3=(\ 5+5+5\ )\ \%\ 19 \\ \therefore 5\ \times_{f}3=15

하지만 일반적인 곱셈 연산과 다르게 결과값이 생각하는 것과 다르게 나옴을 알 수 있다.

1.8.2 유한체 거듭제곱 이해

거듭제곱은 한 숫자를 여러번 곱하는 것이다.

7^3=7\ \times\ 7\ \times\ 7=343

유한체에서도 나머지 연산을 이용하여 거듭제곱을 할 수 있다.
동일하게 $F_{19}$ 에서 정의하면 아래와 같다.

7^3=343\ \%\ 19=1 \\ 9^{12}=7

거듭제곱의 결과 또한 곱셈 연산 결과처럼 일반적인 값과 다른 값이 나온다.
하지만 위에 설명한 바와 같이 유한체 내에서의 연산 결과는 항상 유한체 안에 속해야한다.
곱셈의 결과는 항상 집합 $\{\ 0,\ 1,\ ...\ ,p-1\ \}$ 에 속해야하므로 저런 값이 나오게 된다.

1.9 파이썬을 통한 유한체 곱셈과 거듭제곱 구현

1.9.1 유한체 곱셈 구현

위 설명을 통해 유한체 곱셈의 정의를 이해했다면 FieldElement Class 에서 메소드를 구현해보자.

>>> from ecc import FieldElement
>>> a = FieldElement(3,13)
>>> b = FieldElement(12,13)
>>> c = FieldElement(10,13)
>>> print(a*b==c)
True

그럼 곱셈을 위한 Python 코드로 mul 메소드를 작성해보자.

class FieldElement:
...
	def __mul__(self,other):
		if self.prime != other.prime:
			raise TypeError('Cannot multiply two numbers in differnet Fields')
		num = (self.num * other.num) % self.prime #1
		return self.__class__(num, self.prime)

num 부분의 코드를 직관적으로 해석하면, 곱셈 연산을 통해 나온 결과값을 유한체 연산을 통해 값을 저장함을 보인다는 것을 알 수 있을 것이다.

1.9.2 유한체 거듭제곱 구현

위와 같은 방식으로 거듭제곱도 구현 가능하다.
아래의 빈칸을 채워넣는 형식으로 코드를 완성 해보자.

class FieldElement:
...
	def __pow__(self,exponent):
		num = (                    ) % self.prime
		return self.__class_(num, self.prime)

1.10 유한체 나눗셈

1.10.1 유한체 나눗셈 정의

지금까지 사칙연산중 나눗셈을 제외한 나머지가 유한체에서 어떻게 연산 되는지 설명했다.
하지만 나눗셈은 이와 다르게 일반 대수의 나눗셈과 비교해야한다.
일반 대수에서의 나눗셈은 곱셈의 역연산이다.

7\ \times\ 8=56\ 은 \\ 56\div 8 =7\ 과\ 같다.

이는 유한체 나눗셈에서도 유효하며, 일반 대수와 마찬가지로 0으로 어떠한 값을 나눌 수 없다.

3\ \times_{f}7=21\ \%\ 19=2\ 로부터 \\ 2\ \div_{f}7=3\ 의\ 등식이\ 성립한다.

유한체 $F_{19}$ 에서 이를 적용하면 아래와 같다.

3\ \times_{f}7=21\ \%\ 19=2\ 로부터 \\2\ \div_{f}7=3\ 이\ 성립한다.

9\ \times_{f}5=45\ \%\ 19=7\ 로부터 \\7\ \div_{f}5=9\ 가\ 성립한다.

나눗셈 결과를 보면 일반 수학 상식의 나눗셈과 다른 모습을 보인다는 것을 알 수 있다.
이는 유한체 원소끼리의 나눗셈 연산이기 때문이다.
유한체에서 닫혀 있는 나눗셈이 가능한 이유는 이와 같이 일반 수학 상식과 다르기 때문이다.
그렇다면 $3\ \times_{f}7=2$ 를 모르는 상황에서는 $2\ \div_f7$ 을 어떻게 계산할까?
이는 페르마의 소정리를 통해 항상 아래와 같음을 알 수 있다.

n^{p-1}\ \%\ p=1 \\ 여기서\ p는\ 소수이다.

지금까지 소수를 위수로 하는 유한체를 사용했기 때문에 이 정리를 통해 계산 가능하다.

나눗셈은 사칙연산에서 곱셈의 역연산이기 때문에 아래와 같이 정의 가능하다.

a\ \div\ b = a\ \times_{f}(\ 1\ \div\ b\ )=a\ \times_{f}b^{-1}

\therefore b^{p-1}=1

$p$ 는 소수기이 때문에 요약 정리 하면 아래와 같이 정리 할 수 있다.

b^{-1}=b^{-1}\ \times_{f}1=b^{-1}\ \times_{f}b^{(p-1)}=b^{(p-2)}

\therefore\ b^{-1}=b^{(p-2)}

그렇다면 유한체 $F_{19}$ 에서 0이 아닌 모든 원소에 대해 $b^{18}=1$ 을 의미하게 된다.
따라서 $b^{-1}=b^{17}$ 임을 알 수 있다.

1.10.2 효율적인 유한체 나눗셈

나눗셈은 지수에 따라서 값이 커질 수 있기 때문에 계산 시간이 길어질 수 있다.
이러한 이유때문에 나눗셈 연산은 시간이 가장 많이 걸리는 연산이다.
파이썬에서는 내장함수 pow( ) 를 통하여 거듭제곱을 통해 나눗셈을 구현 가능하다.

>>> pow (2,4,3)
1

>>> pow(2,4) % 3
1

파이썬 pow ( ) 함수의 3번째 인자는 모듈러 연산이기 때문에 나머지가 1이 출력됨을 볼 수 있다.

1.11 유한체 거듭제곱

1.11.1 유한체 거듭제곱 수정

앞서 작성했던 거듭제곱의 메소드를 음의 지수를 처리할 수 있게끔 수정해보자.

>>> from ecc import FieldElement
>>> a = FieldElement(7,13)
>>> b = FieldElement(8,13)
>>> print(a**-3==b)
True

현재 정의한 pow 메소드는 $a^{-3}$ 과 같은 음의 거듭제곱을 사용할 때 오류가 발생한다.
내장함수 pow ( ) 의 정의에 따라 두 번째 매개변수는 반드시 양수여야 하기 때문이다.
이 문제를 해결하기 위해 페르마의 소정리를 활용한다.

a^{p-1} = 1

$a^{p-1}$ 은 항상 $1$ 과 같으므로 $a^{p-1}$ 을 어떠한 수식에든 곱할 수 있다.

a^{-1}=a^{-1}\ \times\ a^{(p-1)}=a^{(p-4)}

위와 같은 식으로 음의 지수를 양의 지수로 변경 가능하며, 코드로 옮기면 아래와 같다.

class FieldElement:
...
	def __pow__(self,exponent)
	n = exponent
	while n<0:
			n+=self.prime-1 #1
	num = pow(self.num, n, self.prime) #2
	return self.__class__(num, self.prime)

위 코드를 주석에 따라 해석하면 아래와 같다.
1. 양의 지수를 얻을 때 까지 self.prime -1 값을 계속 더한다.
2. 계산 효율이 좋은 내장함수 pow ( ) 를 사용하여 계산한다.
하지만 위 코드에서 나머지 연산자를 사용하면 값을 계속 더하거나 while 루프 없이 코드를 작성할 수 있다.

class FieldElement:
...
	def __pow__(self, exponent):
		n = exponent % (self.prime-1) #1
		num = pow(self.num, n, self.prime)
		return self.__class__(num, self.prime)

위 코드를 주석에 따라 해석하면 아래와 같다.
1. exponent 를 $0$ 과 $p-2$ 의 사잇값으로 변환한다.
이런식으로 구현 된 함수는 큰 음수의 지수를 가져도 거듭제곱을 빠르게 실행 가능하다.

alg0r1thm

블록체인 한입

다음 포스트

[밑바닥부터 시작하는 비트코인] 2. 타원곡선

2개의 댓글

Finite field of order 57

2024년 5월 19일

안녕하세요. 유한체 F_{57}는 존재하지 않습니다. 비록 57이 Grothendieck prime이라고 불릴지라도 57은 소수가 아니며 소수의 거듭제곱도 아닙니다. 감사합니다.

1개의 답글