2.1 타원곡선의 필요성
- 이번장에서는 타원곡선암호 ( ECC; Elliptic Curve Cryptography ) 를 이해하기 위해 타원곡선에 대하여 공부한다.
- 비트코인에서는 타원곡선 디지털서명 알고리즘(ECDSA; Elliptic Curve Digital Signature Algorithm) 을 사용하기 때문에 앞서 배운 유한체와 타원곡선에 대한 이해가 필요하다.
2.2 타원곡선의 정의
- 타원곡선은 대수기하학에서 방정식으로 정의되는 대수 곡선을 의미한다.
- 아래와 같이 정의 가능하다.
- 타원곡선 그래프 위의 점들의 집합을 라고 할때, 아래의 조건을 만족한다.
- 에 속한 임의의 점 에 대하여 또한 에 속한다.
- (P+Q)+R=P+(Q+R)$ 이다.
- 이상점 이 있으며, P+0=0+P=P 이다.
- 가 의 역원이면, 이다.
- P+Q=Q+P 이다.
- 비트코인에서 채택한 타원곡선은 secp256k1 이라고 하며, 아래와 같이 정의된다.
2.2.1 방정식이란?
- 그 전에 앞서 등식에 대해서 알아보자
- 위와 같이 두식의 값이 같다고 표현한 식을 등식이라고 한다.
- 위 등식에서는 숫자만 들어있지만 변수와 함께 작성하여 참으로 만드는 변수 값을 찾는것을 방정식이라 한다.
- 위와 같은 형식으로 값이 성립될 때, 방정식이라고 한다.
- 이 때의 식이 성립되도록 하는 의 값을 방정식의 해 라고 한다.
2.2.2 1차방정식
- 위에서 설명한 방정식과 유사한 형태로 다른 식을 구성할 수 있다.
- 아래는 1차방정식의 형태이다.
- 위 식은 아래 그래프와 같은 형태로 나타낼 수 있다.
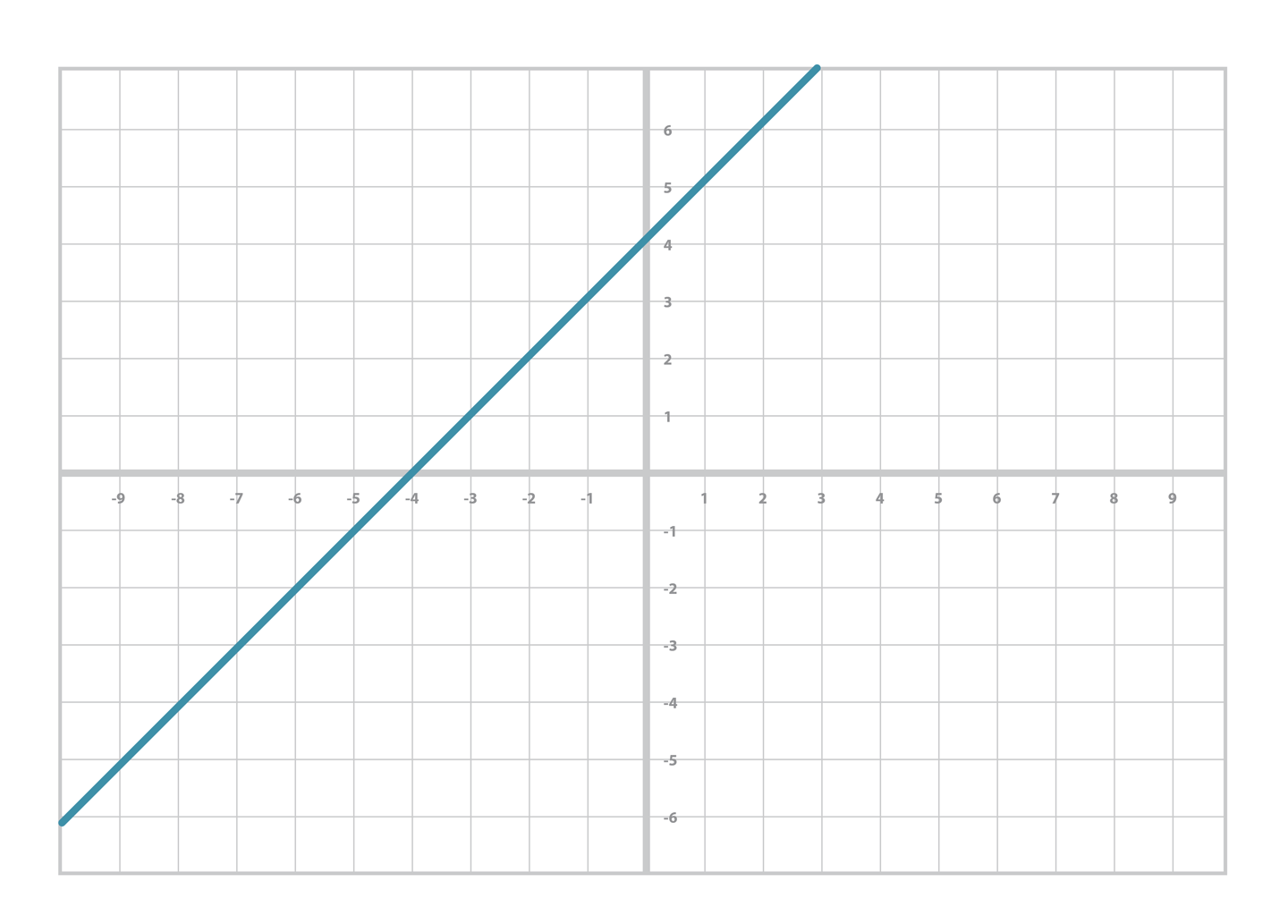
- 1차방정식은 직선으로 나타낼 수 있으며, 기울기와 절편값에 따라 그래프의 형태가 달라진다.
2.2.3 2차방정식
- 2차방정식은 위 1차방정식의 미지수 의 지수를 올려 아래와 같이 작성 가능하다.
- 또한 위 식을 그래프로 그리면 아래와 같은 형태로 나타낼 수 있다.
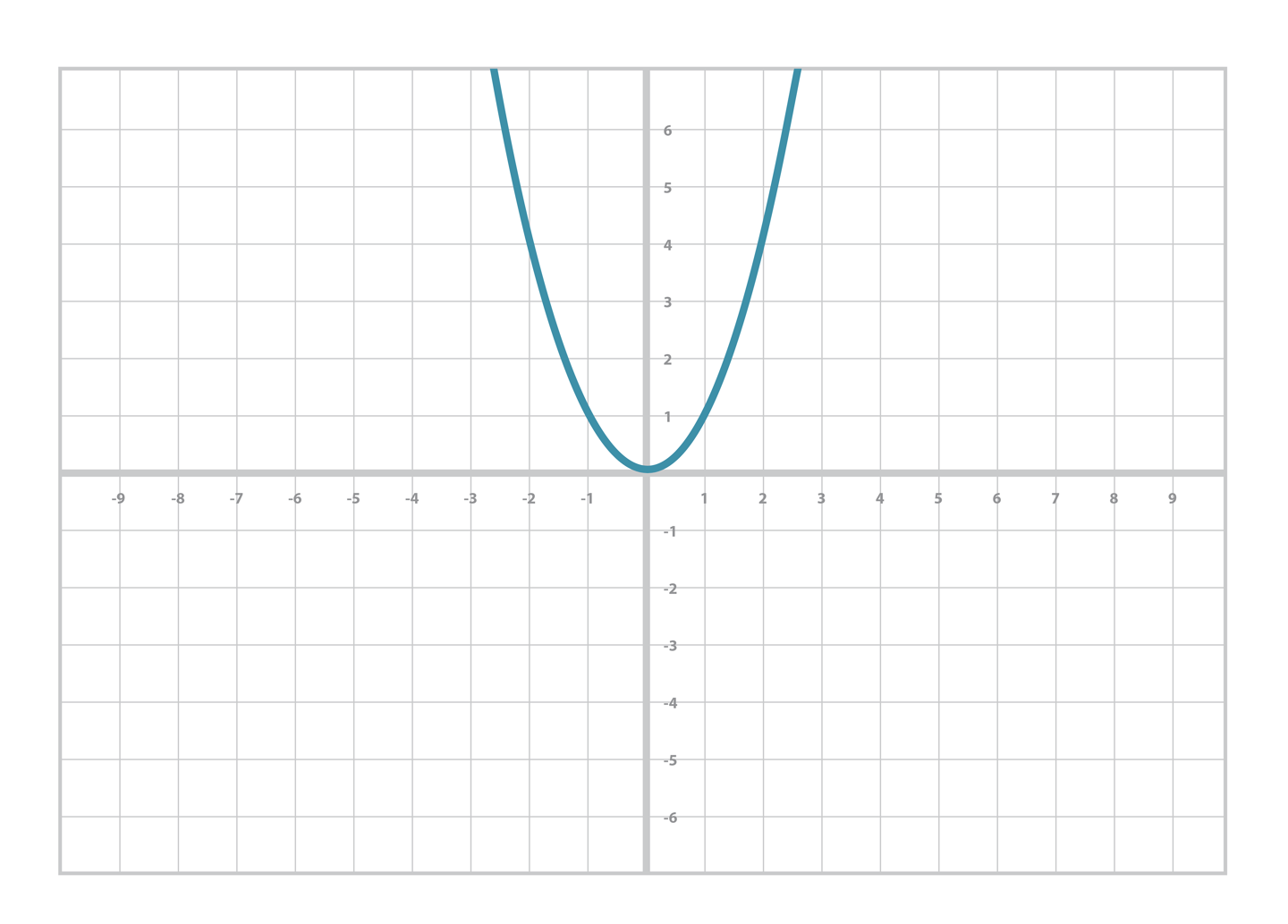
- 2차방정식은 위와 같이 곡선으로 나타낼 수 있으며, 이때의 곡선을 이차곡선 이라고 한다.
2.2.4 3차방정식
- 그럼 위 예시와 같이 미지수 의 차수를 3차로 올릴 때 아래와 같이 표현 가능하다.
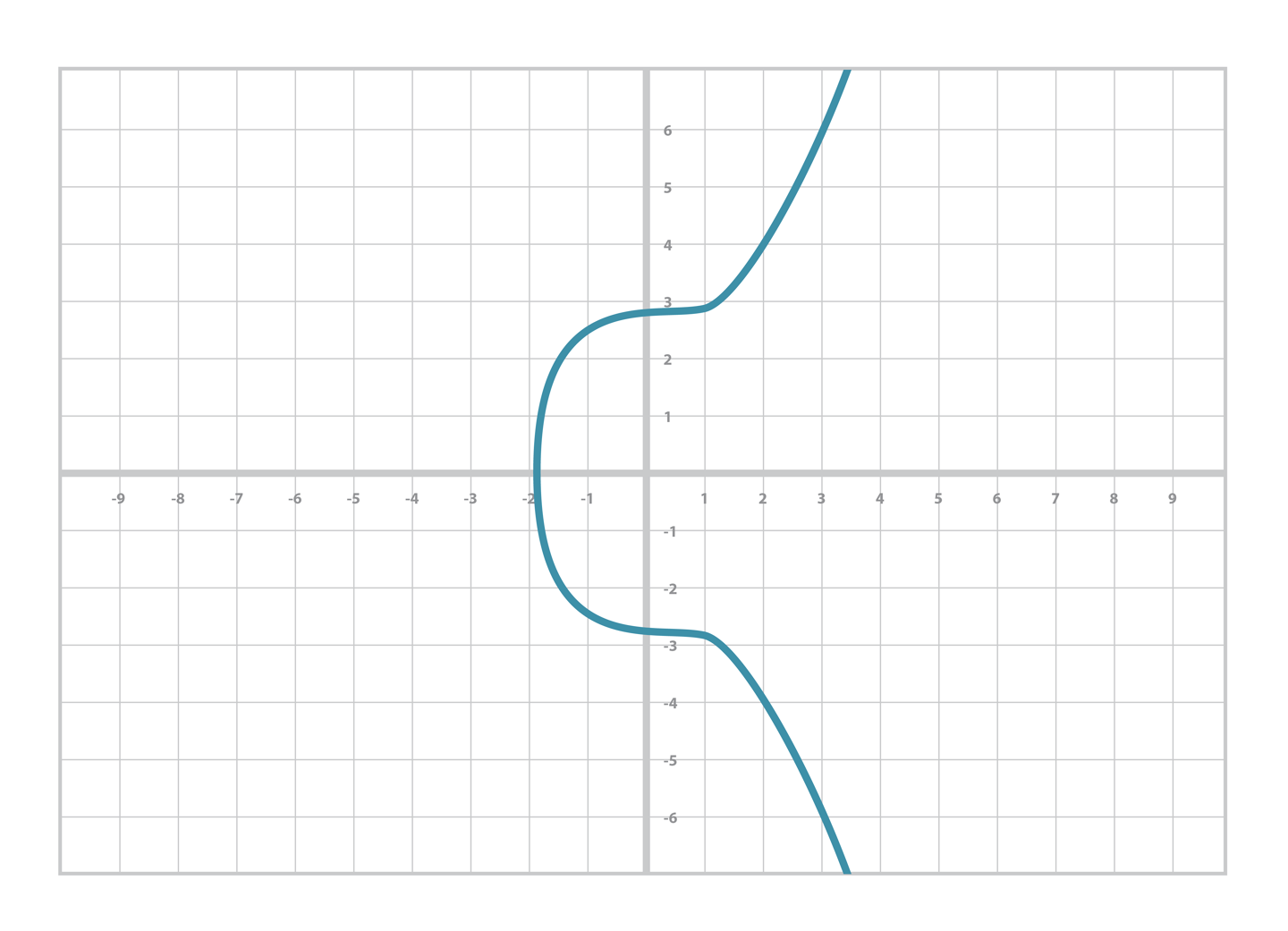
- 위의 수식을 그래프로 표현하면 아래와 같다.
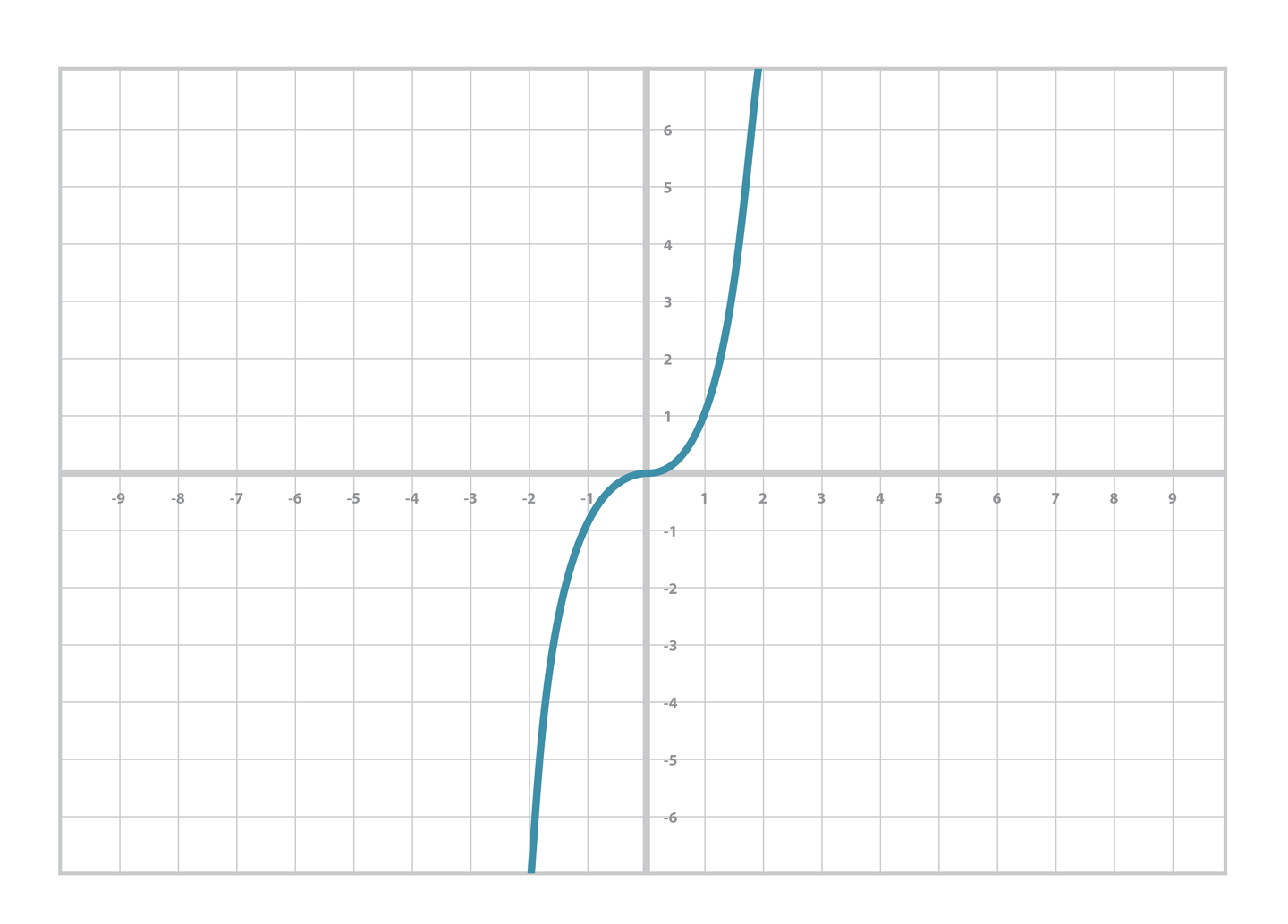
- 그래프의 형태를 보면 극한으로 발산하는 형태를 볼 수 있다.
2.2.5 타원곡선 방정식
- 타원곡선의 형태도 위와 크게 다르지 않다.
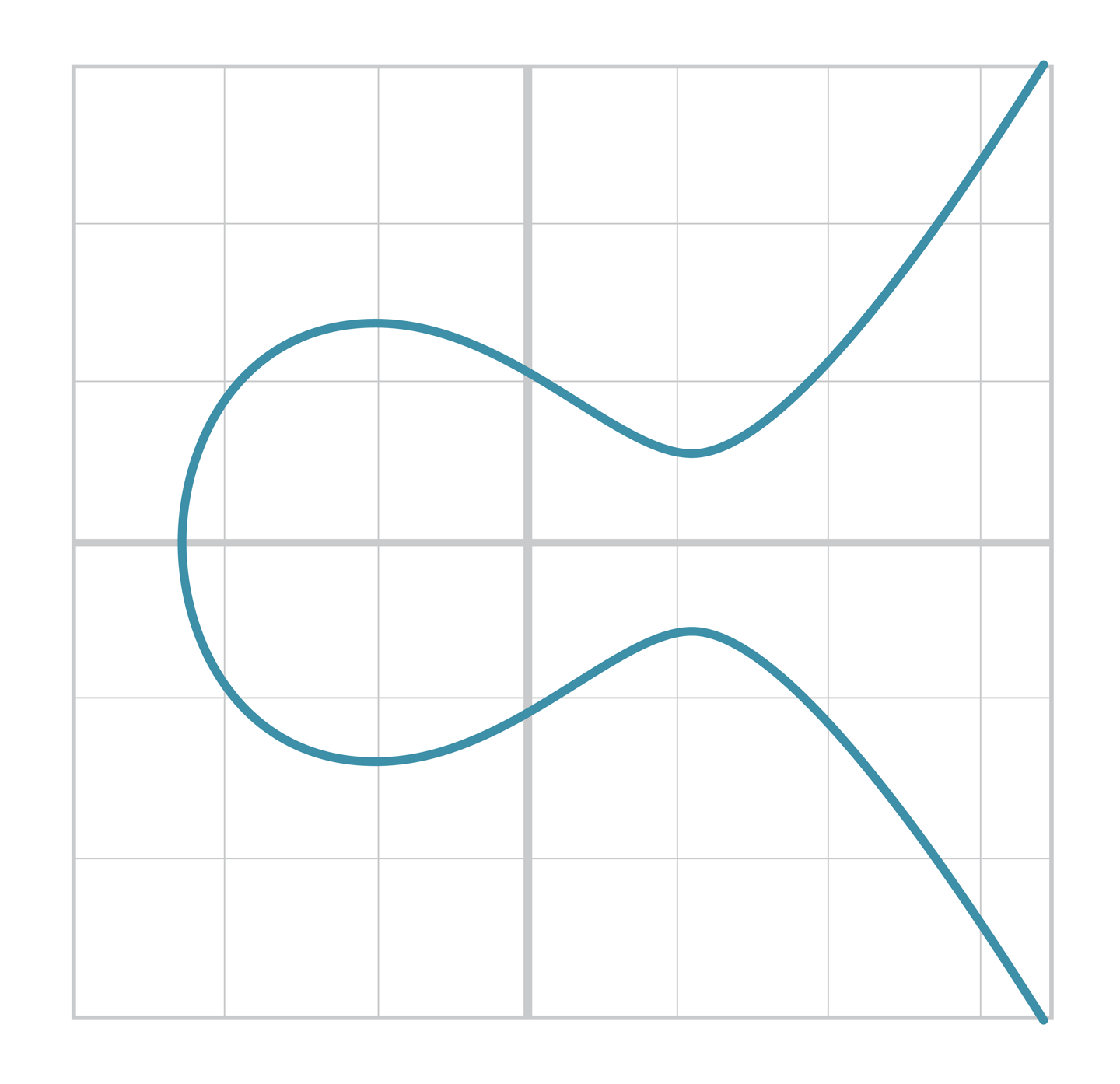
- 위 식을 그래프의 형태로 표현하면 아래와 같다.
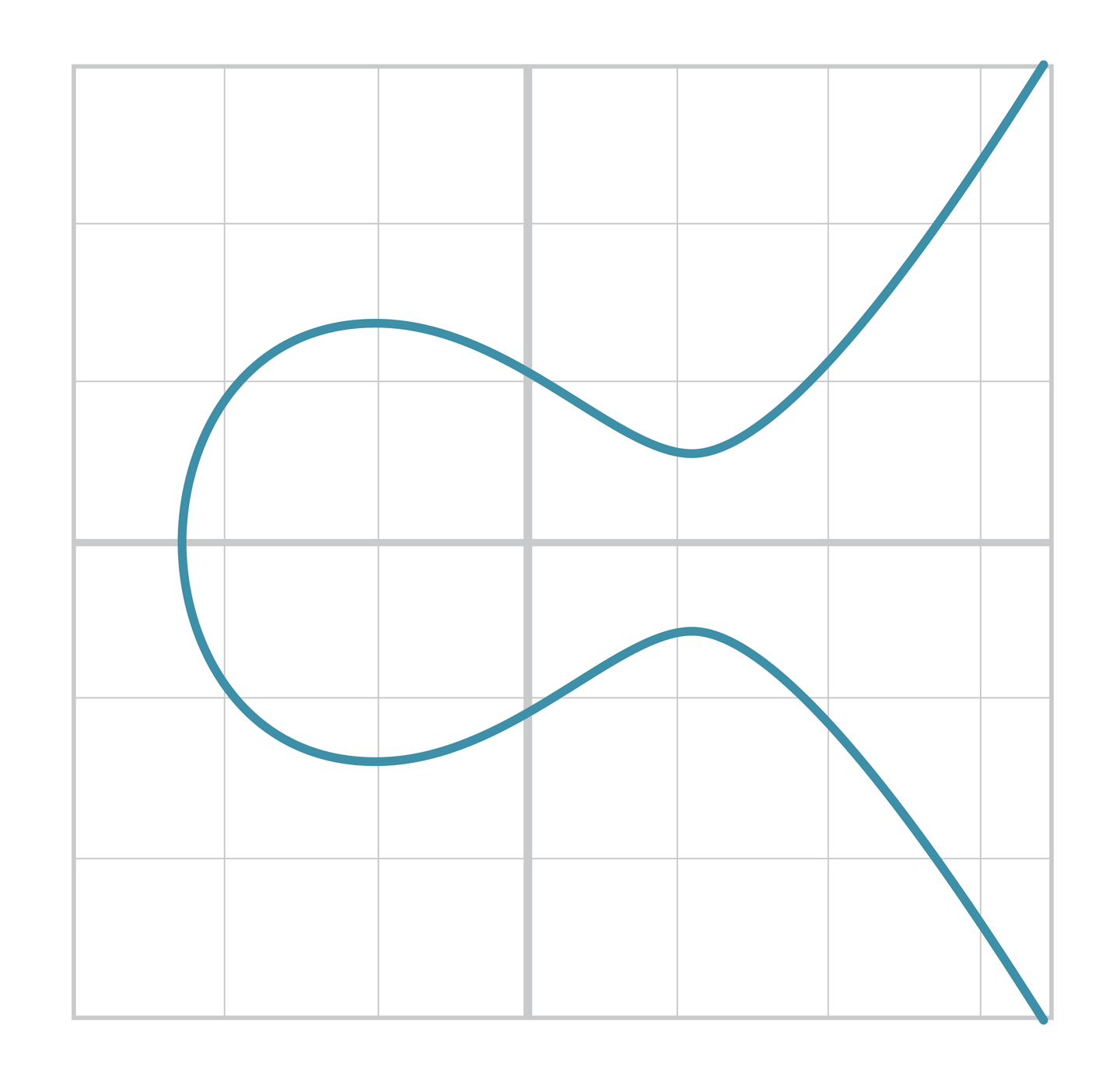
- 타원곡선과 위 3차방정식의 차이는 왼쪽 항에 있다.
- 으로 인해 그래프가 축에 대칭인 모습을 볼 수 있다.
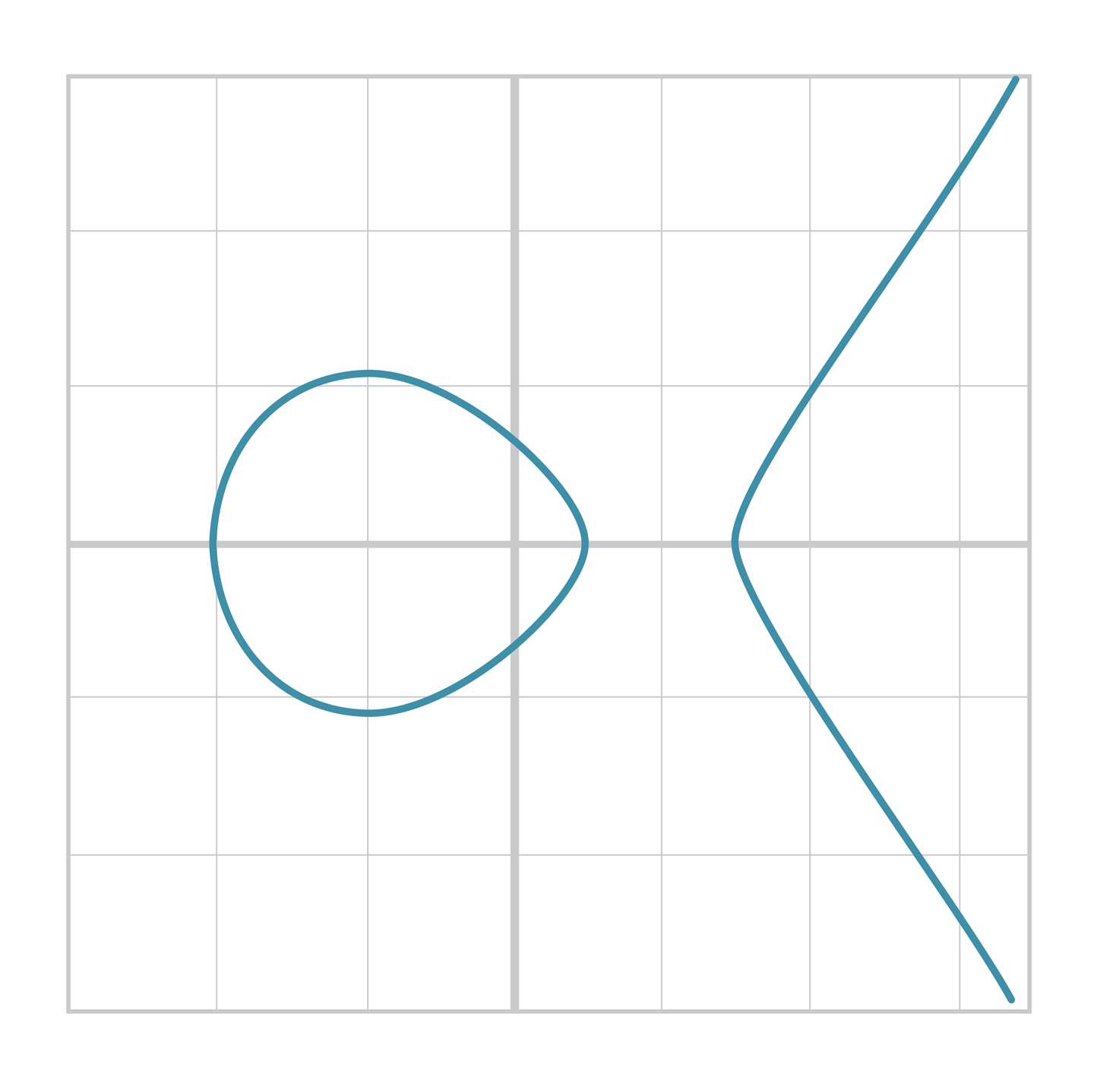
- 타원곡선은 3차방정식의 그래프보다 기울기가 완만한 모습을 볼 수 있는데, 이 또한 왼쪽 항 때문이다.
- 계수의 값에 따라서 곡선이 하나로 이어지지 않고 분리되는 모습을 보이기도 한다.
2.2.6 3차방정식 그래프로 타원곡선 그래프 유도
- 아래 [그림8] 의 3차방정식 그래프로부터 타원곡선 그래프의 형태로 유도해보자.
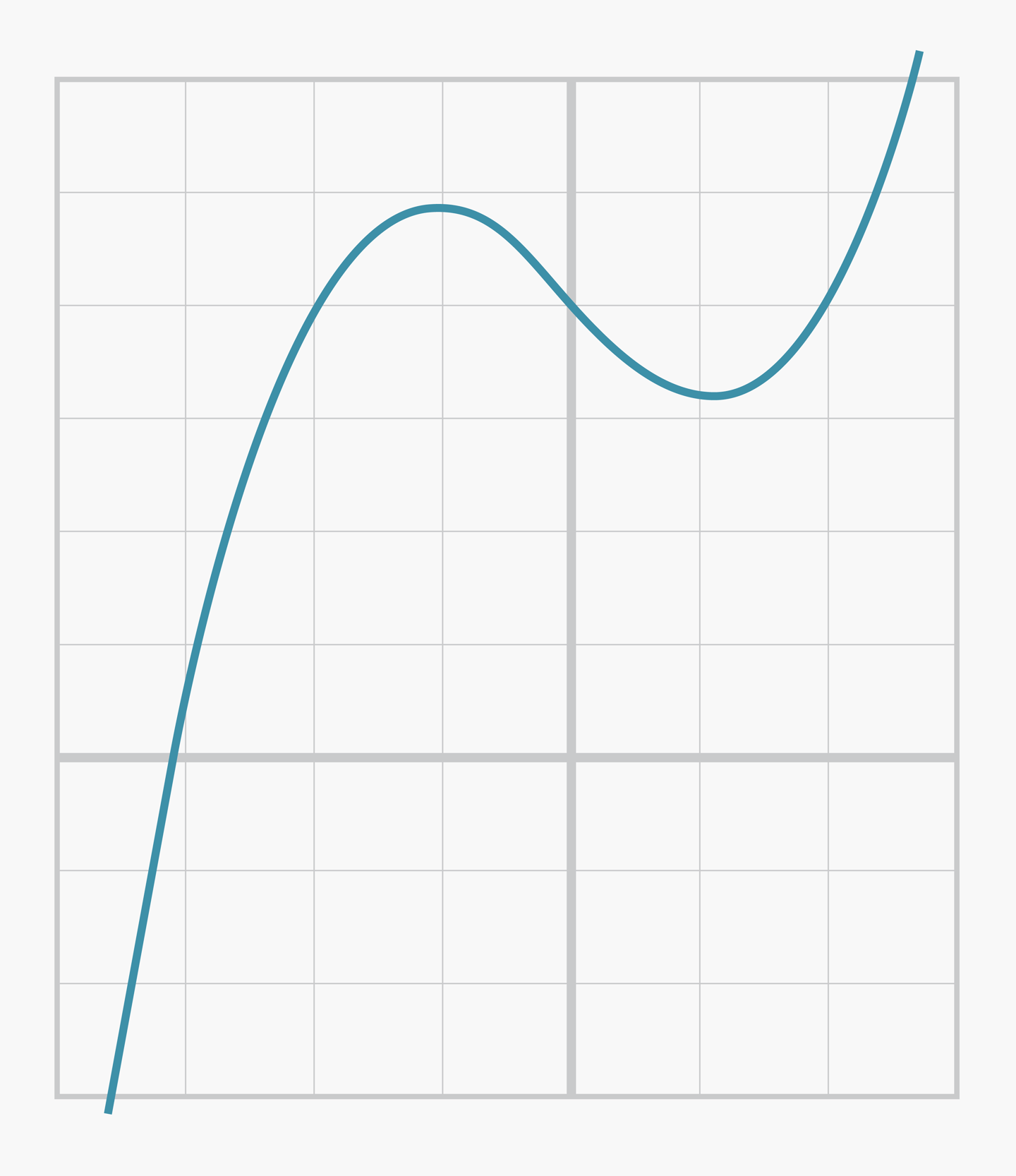
- 위 3차방정식의 그래프에서 인 부분에 대하여 곡선을 완만하게 만들면서 타원곡선 그래프의 형태로 만들어보자.
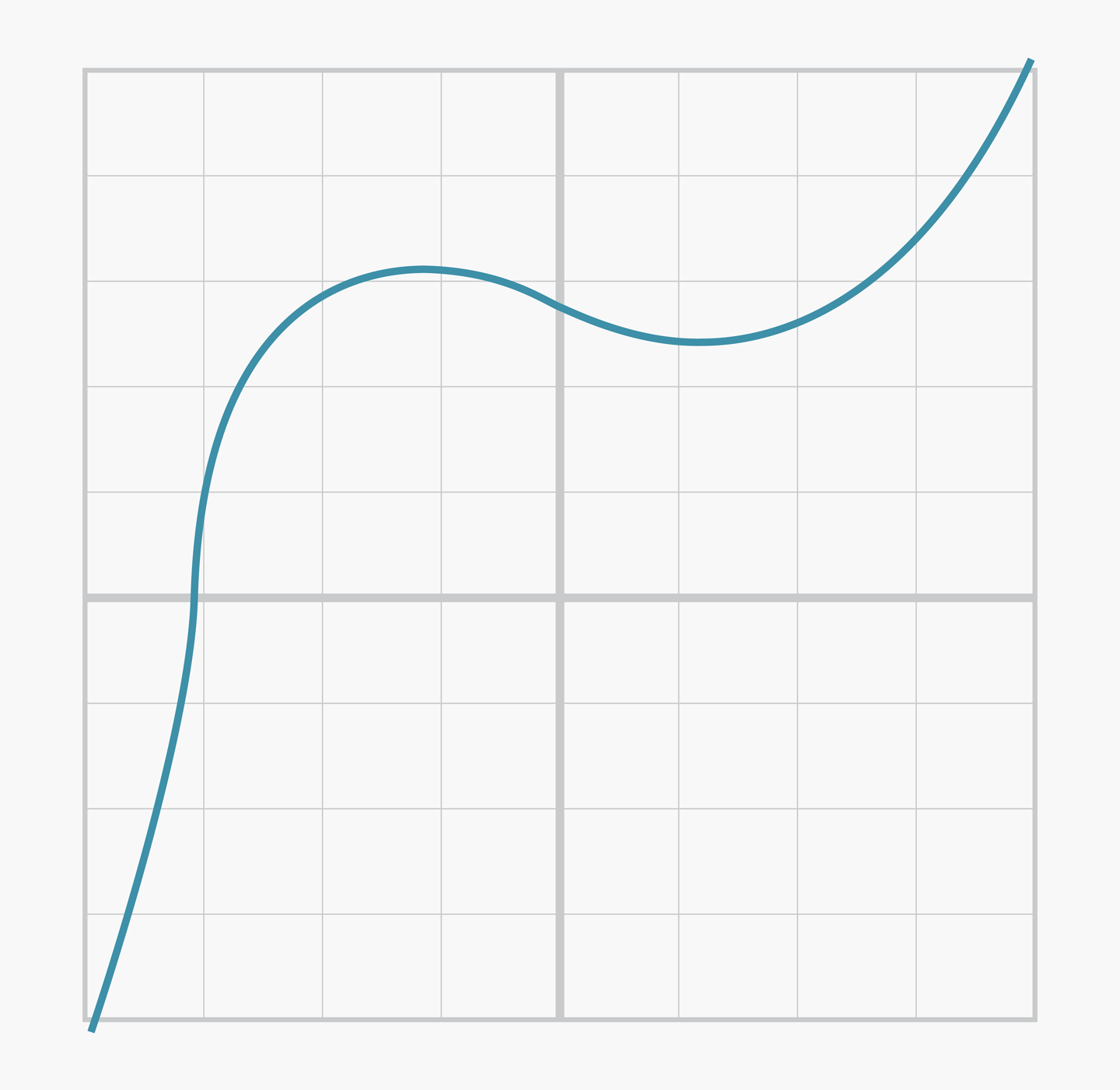
- 완만하게 만들어진 그래프를 인 부분에 대하여 축에 대칭인 그래프로 만들면 타원곡선의 형태가 나온다.
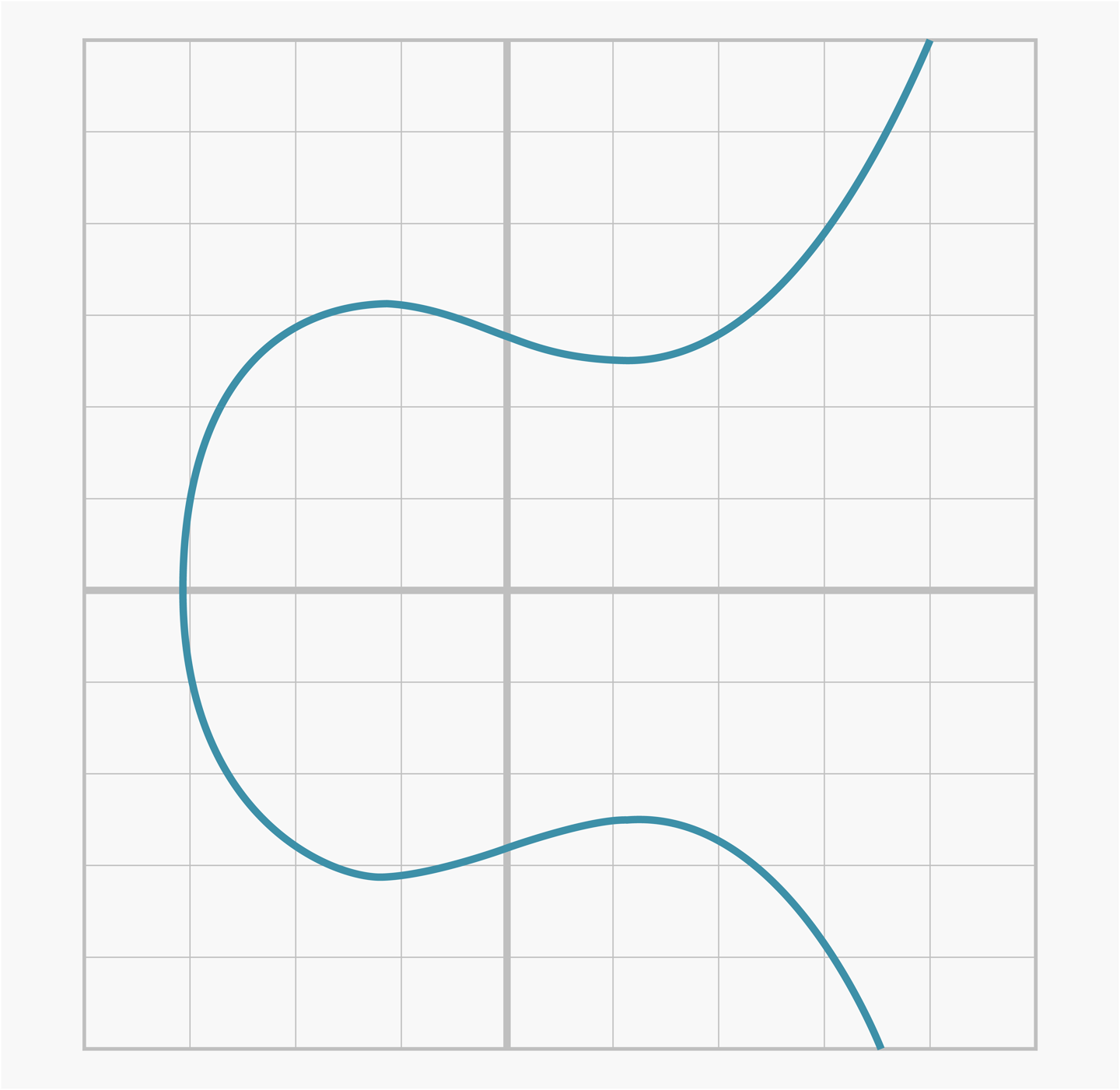
- 비트코인에서 사용되는 타원곡선은 secp256k1 이라고 하며 아래와 같은 방정식으로 표현한다.
- 일반 정규식에서 계숫값이 인 곡선으로 정의되며 아래와 같다.
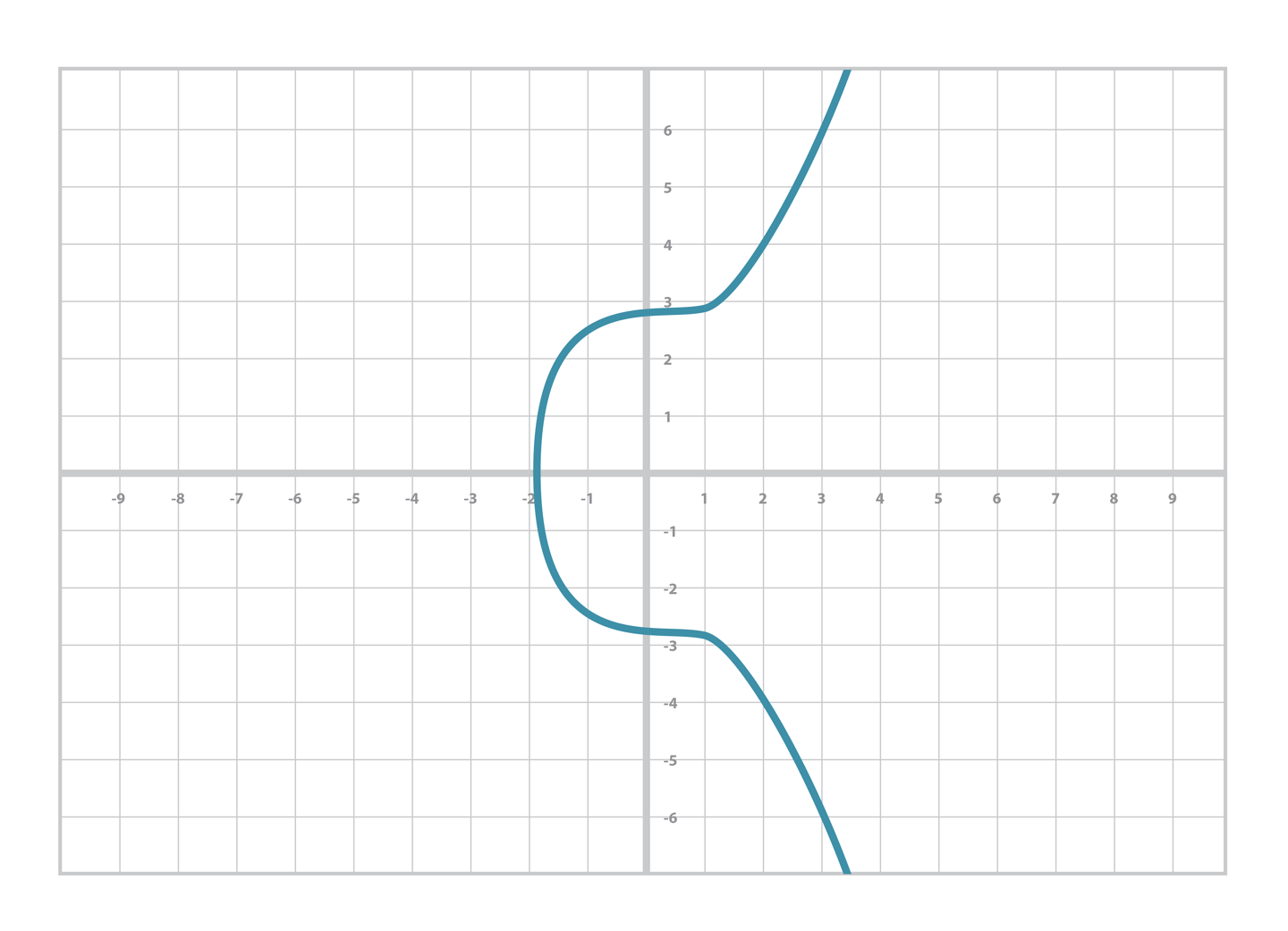
2.3 파이썬을 통한 타원곡선 코딩
- 타원곡선 자체에 대한 내용보단 곡선 위의 개별 점들이 중점적으로 파악해야할 부분이다.
- 이는 이어서 나오는 내용을 보면서 의미가 분명해질 것이다.
- 우선 특정 한 점으로부터 클래스를 정의해보자
- 위와같은 일반형 곡선의 형태로 각각의 계수값으로 곡선을 특정해보자
class Point:
def __init__(self,x,y,a,b):
self.a = a
self.b = b
self.x = x
self.y = y
if self.y**2 != self.x**3 + a * x + b: #1
raise ValueError('({}, {}) is not on the curve'.format(x,y))
def __eq__(self,other): #2
return self.x == other.x and self.y == other.y \
and self.a == other.a and self.b == other.b- 주석표시된 부분을 중점으로 코드를 설명하면 아래와 같다
- 그래프 위의 점들의 집합 안에 점이 존재하는지 검사한다.
- 집합 안에 있는 점 가 존재하고, 그 좌표값들이 각각 동일한지 판정한다.
>>> from ecc import Point
>>> p1 = Point(-1,-1,5,7)
>>> p2 = Point(-1,-2,5,7)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "ecc.py", line 143, in __init__
raise ValueError('({}, {}) is not on the cureve'.format(self.x, self.y))
ValueError: (-1, -2) is not on the curve- 점이 곡선 위에 존재하지 않기 때문에 init 생성자 메소드에서 예외가 발생함을 볼 수 있다.
2.4 타원곡선에서의 두 점의 덧셈
- 타원곡선의 두 점의 덧셈을 정의하기 위해 어떠한 연산을 거치는지 알아보자.
- 이 연산 과정은 일반적인 덧셈 연산과 어느정도 공통점을 가지기 때문에 점과 점의 덧셈이라고 한다.
2.4.1 직선과 타원곡선의 관계
-
일반적으로 모든 타원곡선에 대하여 몇가지 예외를 제외하면 반드시 아래와 같다.
- 곡선과 함께 그려진 직선은 반드시 곡선과 한 점에서 만난다.
- 곡선과 함께 그려진 직선은 반드시 곡선과 세 점에서 만난다.
-
곡선과 한 점에서 만나는 경우
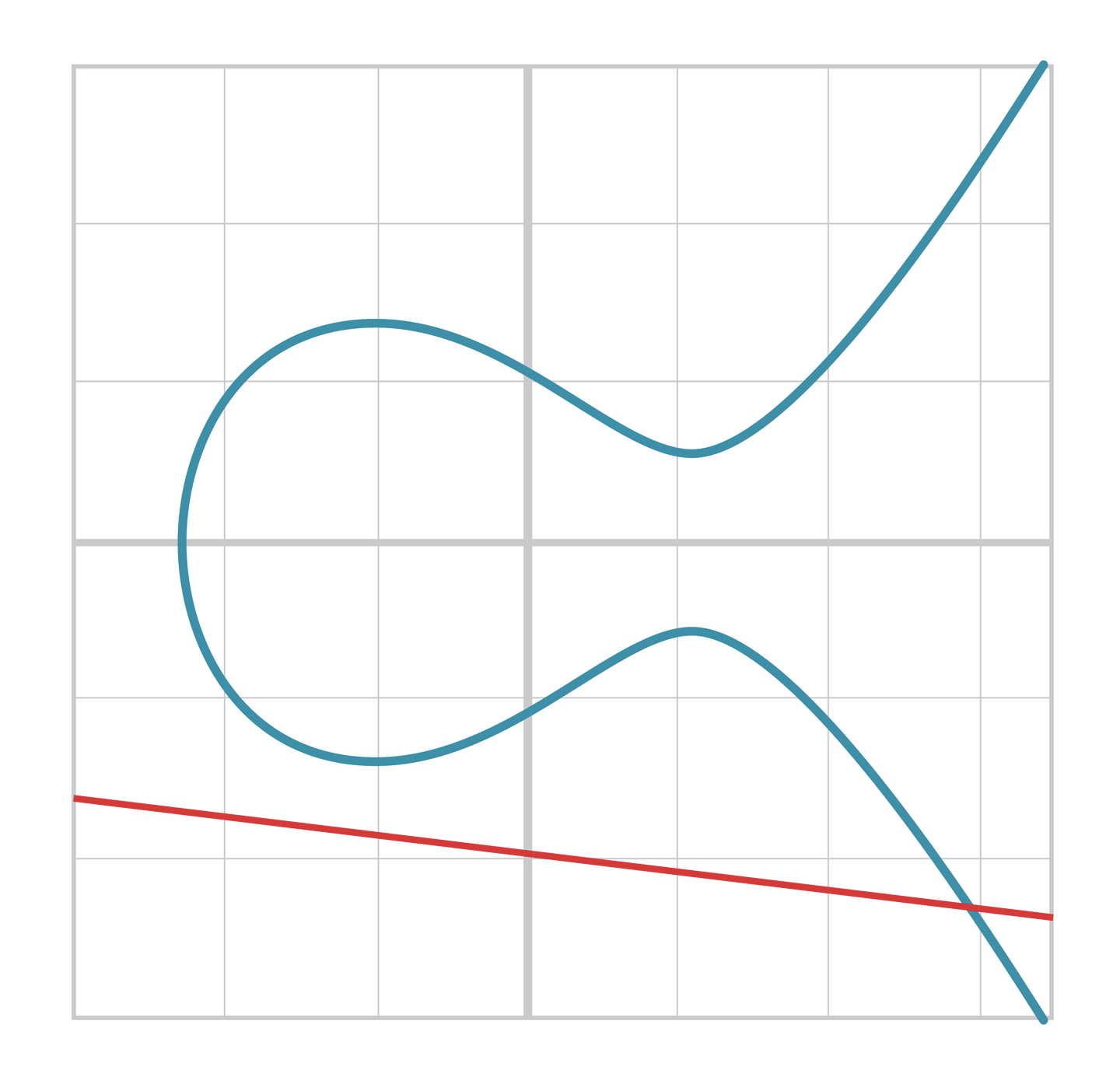
-
곡선과 세 점에서 만나는 경우
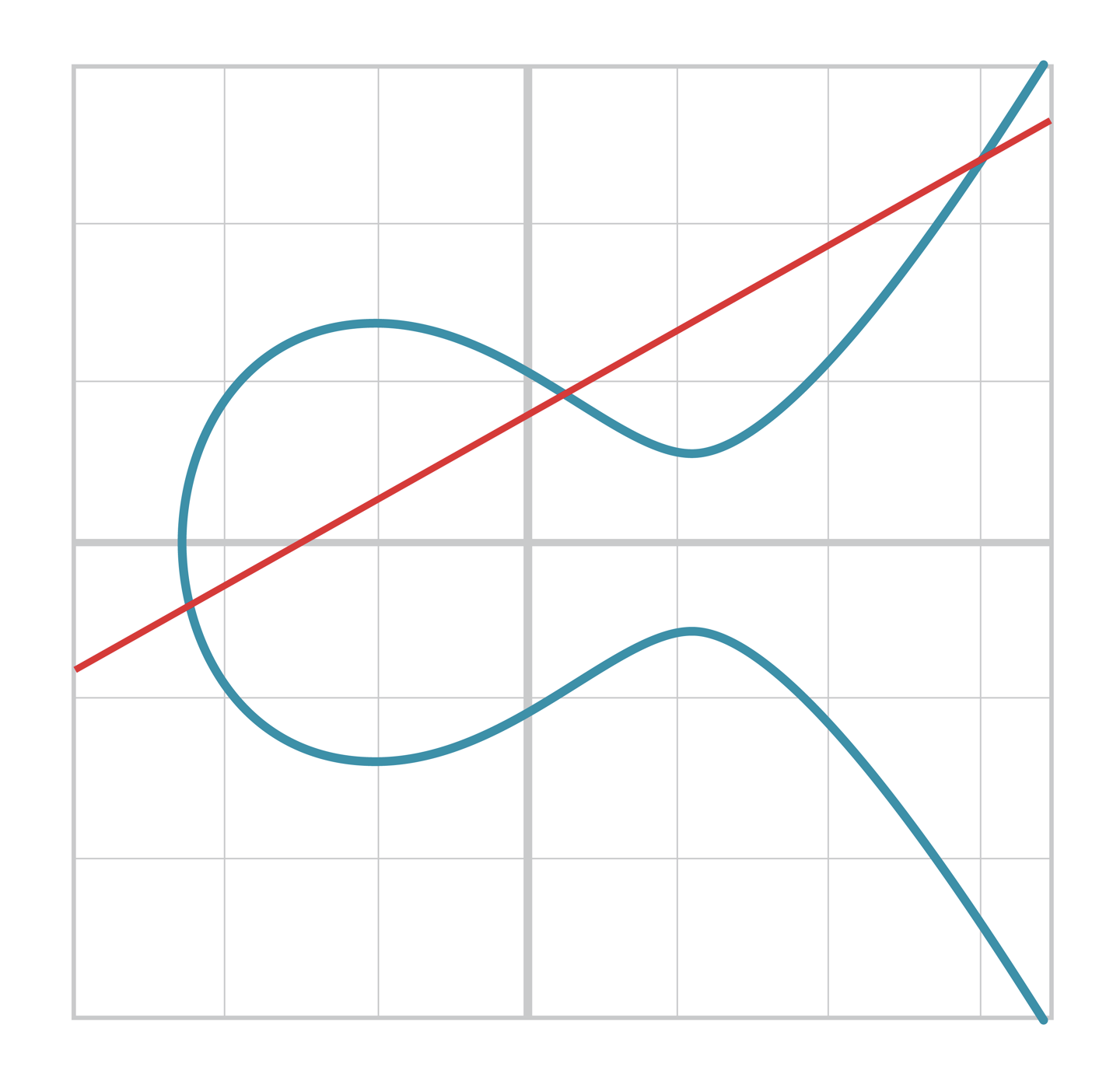
-
곡선의 한 점에 접하는 접선인 경우
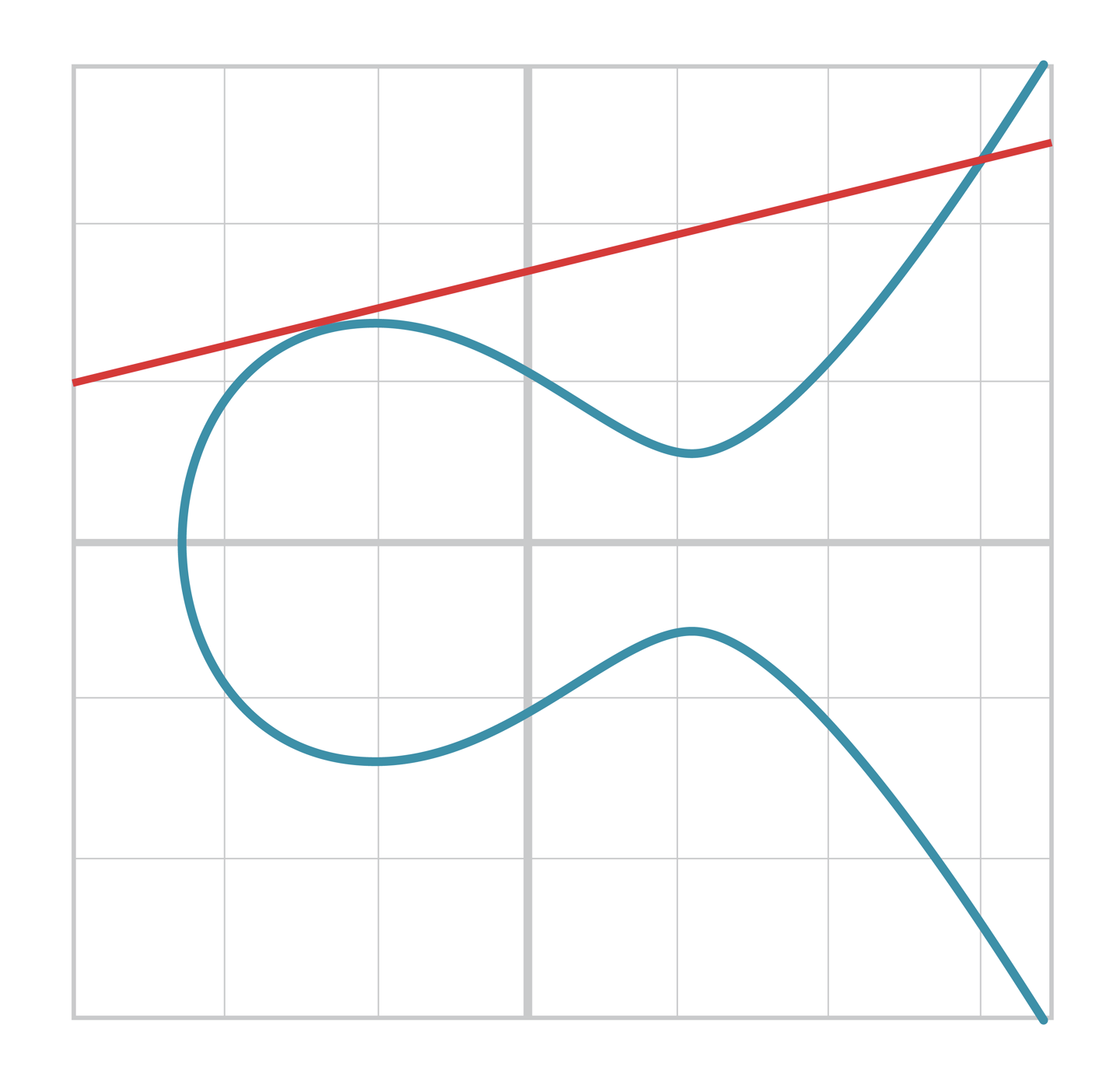
2.4.2 점 덧셈의 정의
- 타원곡선에서 점 덧셈 방법은 아래와 같다.
- 두 점 와 를 지나가는 직선이 타원곡선과 새롭게 만나는 점 를 찾는다.
- 그 점과 축에 대하여 대칭인 점이 덧셈의 결과 이다.
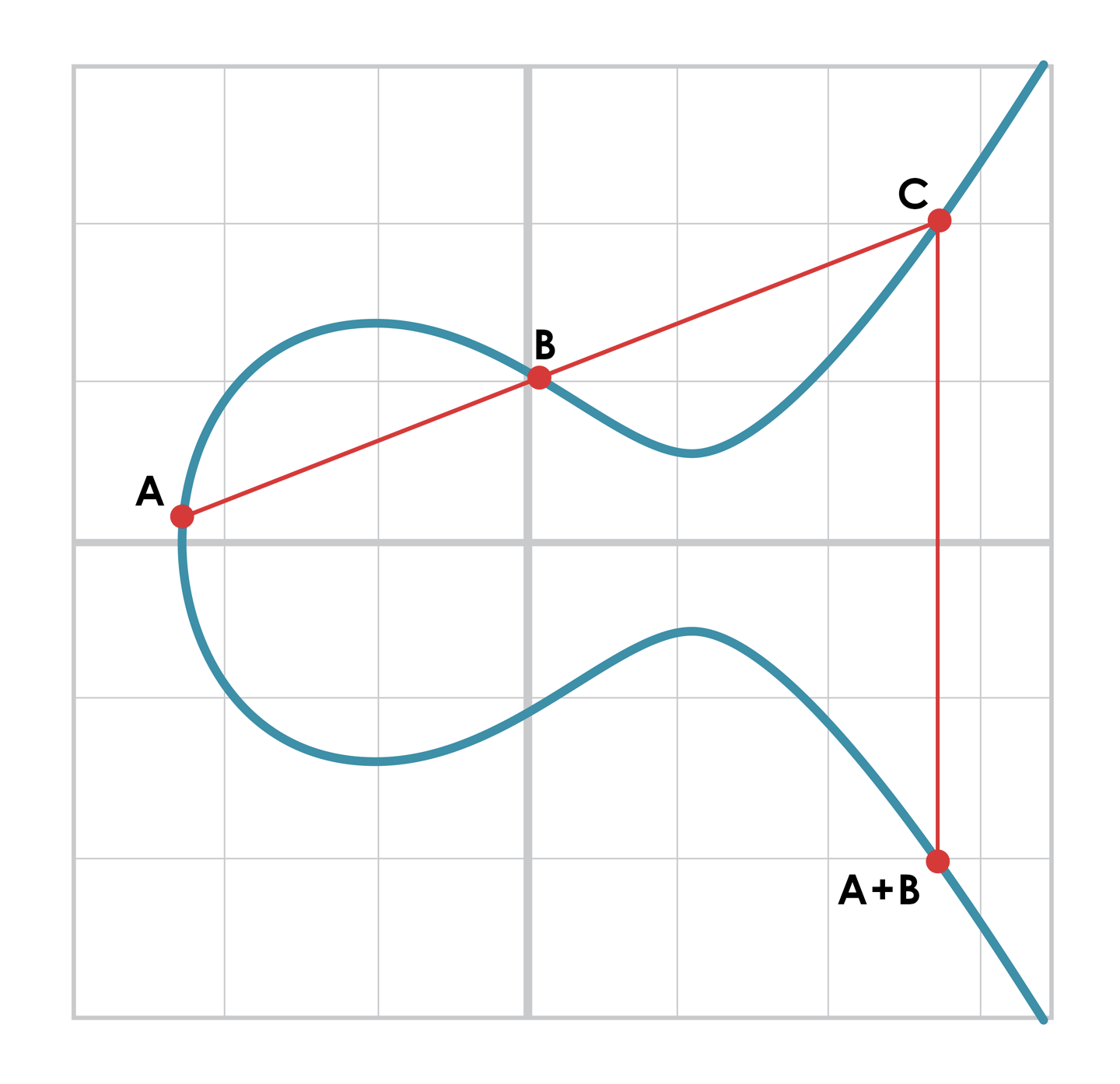
- 이를 통해 아래와 같이 점 덧셈에 대하여 정의가 가능하다.
- 점 덧셈의 결과를 쉽게 예측할 수 없다.
- 점 덧셈은 비선형 연산이다.
2.4.3 점 덧셈의 성질
- 점 덧셈은 일반 덧셈 연산과 유사한 성질을 만족한다.
- 항등원이 존재한다.
- 교환법칙이 성립한다.
- 결합법칙이 성립한다.
- 역원이 존재한다.
- 여기서 항등원이란, 대수의 과 같은 의미의 점이 존재한다는 뜻이다.
- 곡선 위의 라는 점이 존재하고, 라는 점과 더한 결과는 가 된다.
-
이 때의 점을 무한원점 이라고 한다.
- 이는 덧셈에 대한 역원과도 관련이 있다.
- 어떤 라는 점에 대하여 라는 점이 존재하고, 그 합은 항등원이 된다는 것이다.
- 다시 말해 로 정의 할 수 있다는 것**이다.
-
그래프로 볼 때, 이 점들은 축에 수직인 직선과 곡선의 교점이다.
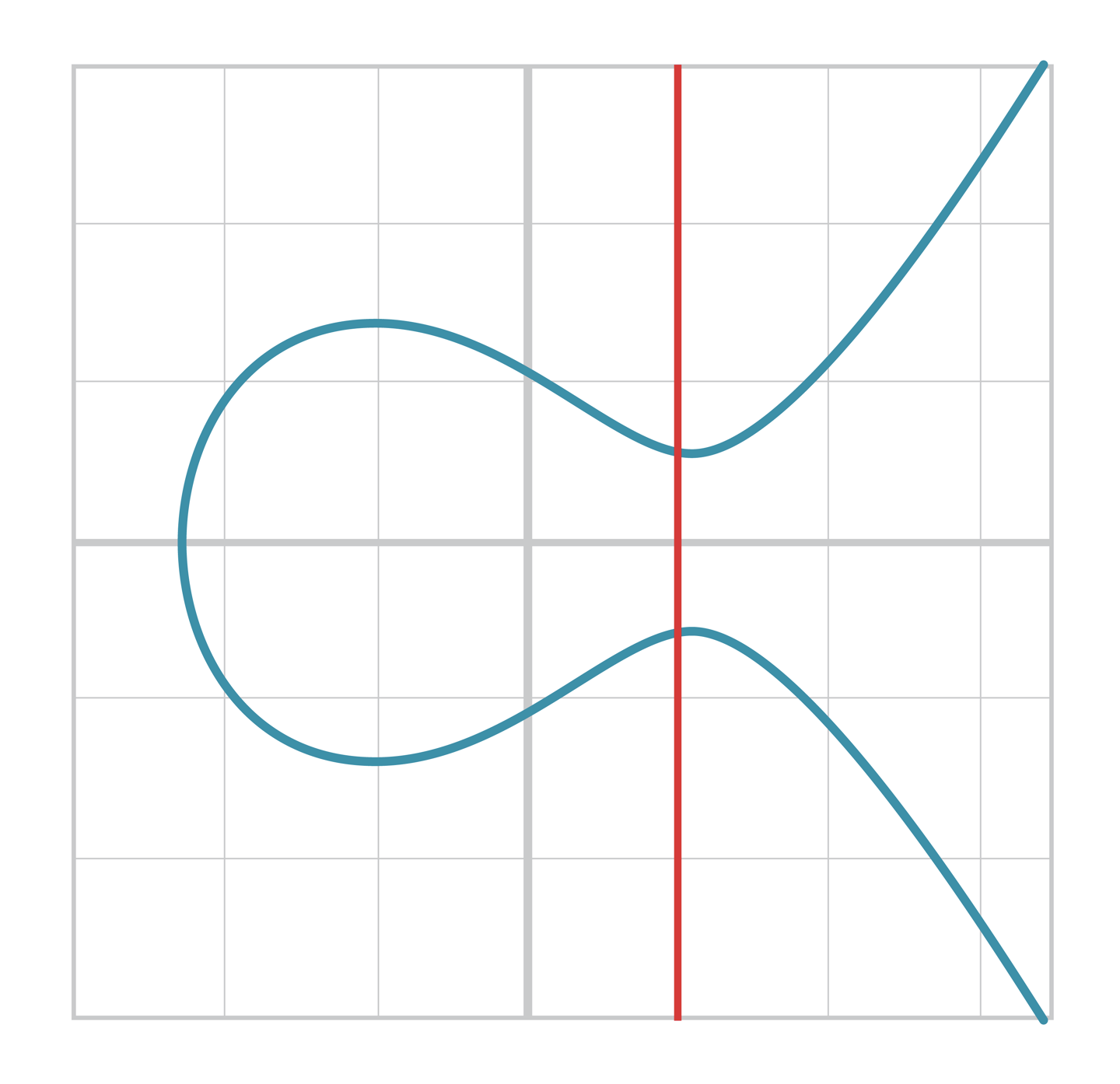
-
축에 수직인 직선과 타원곡선이 만나는 세 번째 점은 영원히 만나지 않으므로 무한대에 있다.
- 이러한 성질때문에 무한원점이라고 부른다.
-
교환법칙
- 연산 순서를 바꿔도 결과가 같다는 뜻이다.
- 와 를 지나는 직선은 순서를 바꿔도 동일한 위치에서 곡선과 만난다.
-
결합법칙
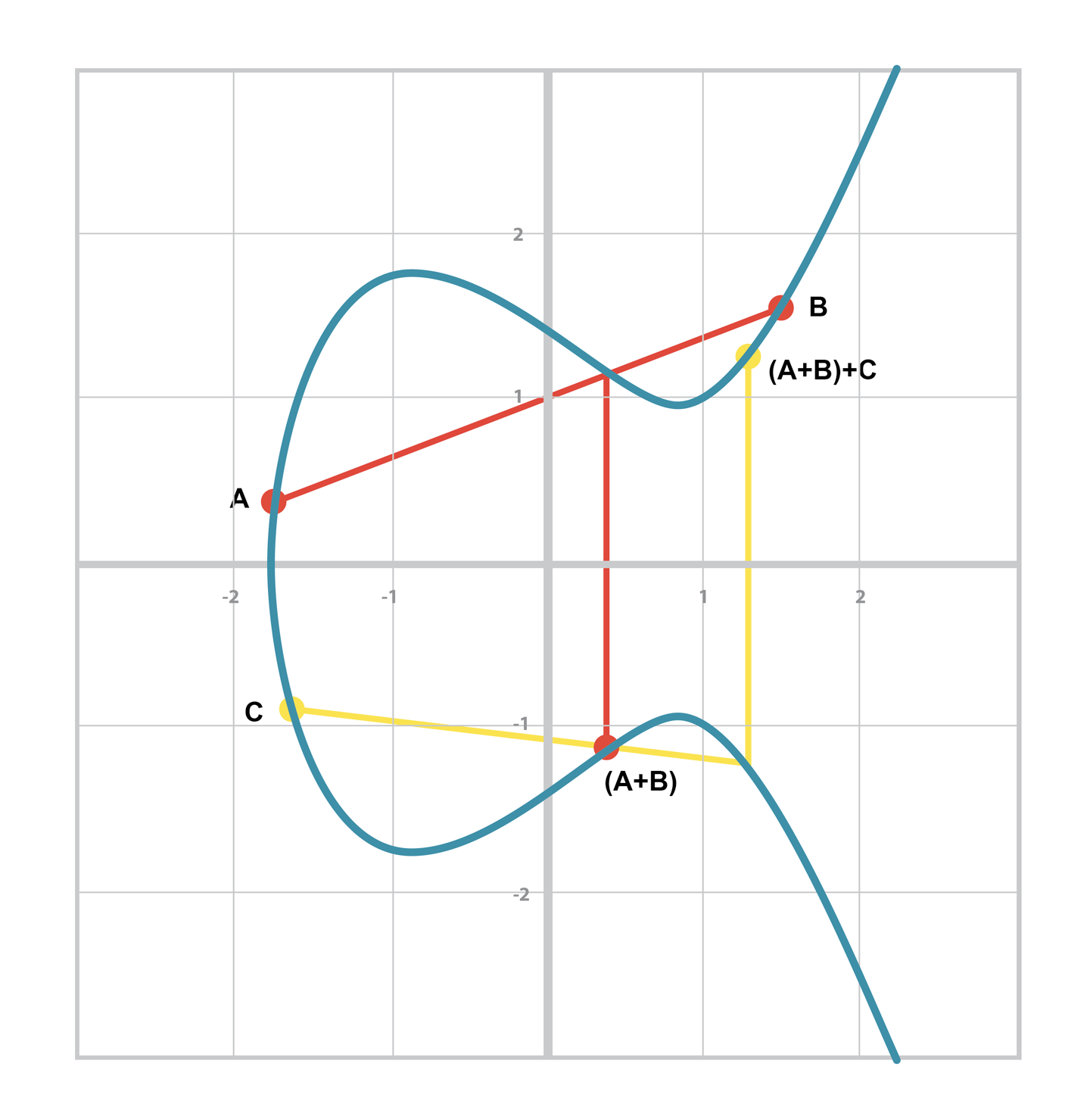
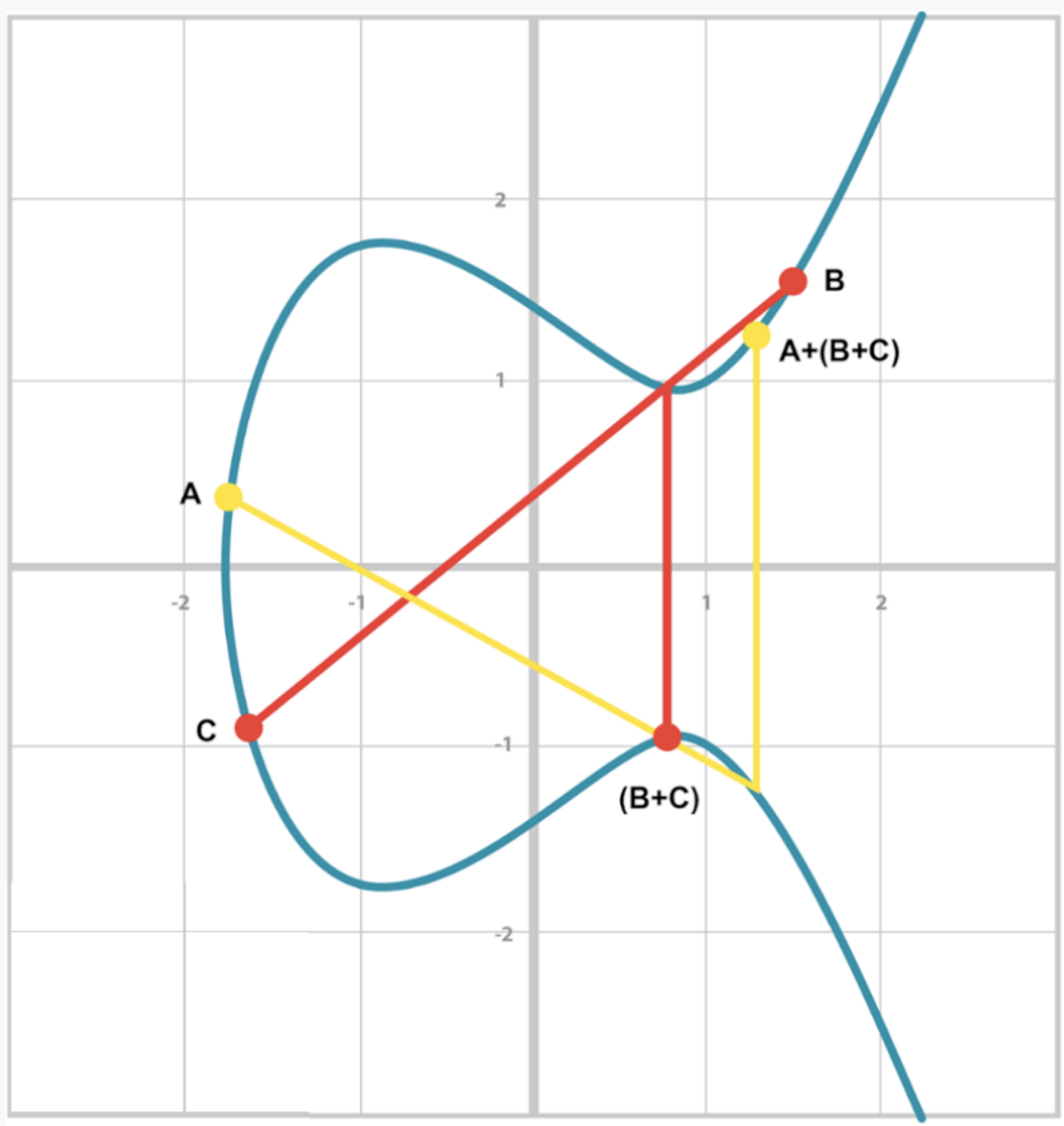
- 3개 이상의 덧셈에서 어느 두 항을 먼저 더해도 결과가 동일하다는 뜻이다.
-
위 연산을 통한 최종 결과는 아래와 같다.
2.5 파이썬을 통한 점 덧셈 구현
- 우선 점 덧셈을 구현하기 위하여 더하는 두 점을 기준으로 세가지 경우로 나누어보자.
- 두 점이 축에 수직인 직선 위에 있는 경우
- 두 점이 축에 수직인 직선 위에 있지 않은 경우
- 두 점이 같은 경우
2.5.1 무한원점 정의
- 항등원에 해당하는 무한원점부터 시작해보자.
- 파이썬에서 무한대 값을 표현하는 것은 쉽지 않기 때문에 None 값으로 정의한다.
>>> from ecc import Point
>>> p1 = Point(-1,-1,5,7)
>>> p2 = Point(-1,1,5,7)
>>> inf = Point(None,None,5,7)
>>>print(p1+inf)
Point(-1,-1)_5_7
>>>print(inf+p2)
Point(-1,1)_5_7
>>>print(p1+p2)
Point(infinity)-
위와 같이 실행되기 위해서는 앞서 작성한 클래스에서 두가지가 추가되어야한다.
- 무한원점을 의미하는 None 값이 인수로 들어올 때, 이후 방정식 로직을 확인하지 않도록 해야한다.
- FieldElement 클래스처럼 덧셈 연산자를 정의해야한다.
-
각각의 조건을 만족하기 위해 init 메소드를 수정하고 add 메소드를 추가하자.
class Point:
def __init__(self,x,y,a,b):
self.a = a
self.b = b
self.x = x
self.y = y
if self.x is None and self.y is None: #1
return
if self.y**2 != self.x**3 + a * x + b:
raise ValueError('({}, {}) is not on the curve'.format(x,y))
def __add__(self,other): #2
if self.a != other.a or self.b != other.b:
raise TypeError('Points {}, {} are not on the same curve'.format
(self,other))
if self.x is None: #4
return other
if other.x is None: #4
return self- 주석표시된 부분을 중점으로 코드를 설명하면 아래와 같다
- None 값을 가지는 의 좌표값은 무한원점을 의미하므로 조건문 실행 이전에 리턴한다.
리턴하지 않을 경우에는 다음 조건문에서 ValueError 가 발생한다. - add 메소드 정의를 통해 연산자를 재정의**한다.
- self.x 가 None 이라는 것을 통해 self 가 덧셈에 대한 항등원 ( 무한원점 ) 임을 뜻하므로 other를
반환한다. - 3번과 동일하게 other가 항등원임을 뜻하므로 self를 반환한다.
- None 값을 가지는 의 좌표값은 무한원점을 의미하므로 조건문 실행 이전에 리턴한다.
2.5.2 ≠ 인 경우
-
축에 대하여 수직인 직선을 위에서 구현했으니 두 점이 다른 경우를 생각해보자.
-
가 다른 두 점의 덧셈은 공식을 통해 해결 가능하다.
-
먼저 두 점을 지나는 직선의 기울기를 유도한다.
-
점 덧셈에 대한 결과값은 기울기로 구한 점을 축에 대해 대칭한 것이다.
-
따라서 는 직선이 곡선과 만나는 교점의 값과 반대 부호를 가지게 된다.
-
그럼 위 공식을 이용하여 add 메소드를 수정해보자.
class Point:
...
def __add__(self,other):
...
if self.x != other.x:
s = (other.y - self.y) / (other.x - self.x)
x = s**2 - self.x - other.x
y = s * (self.x - x) - self.y
return self.__class__(x,y,self.a,self.b)2.5.3 = 인 경우
- 두 점의 좌표는 같고 좌표는 다른 경우 두 점은 축을 사이에 두고 서로 대칭구조를 이룬다.
- 이를 수식으로 표현하면 아래와 같다.
- 이런 경우는 아래와 같은 코드로 구현 가능하다.
class Point:
...
if self.x == other.x and self.y != other.y:
return self.__class__(None, None, self.a, self.b)- 하지만 인 경우는 위와 다르게 두 점을 이은 직선일 때에는 그 점에서의 접선을 의미하게 된다.
- 따라서 그래프 위의 점 에서 접하는 접선을 계산해야한다.
- 이는 접선이 곡선의 다른 부분에서 만나는 교점을 찾아야 함을 의미한다.
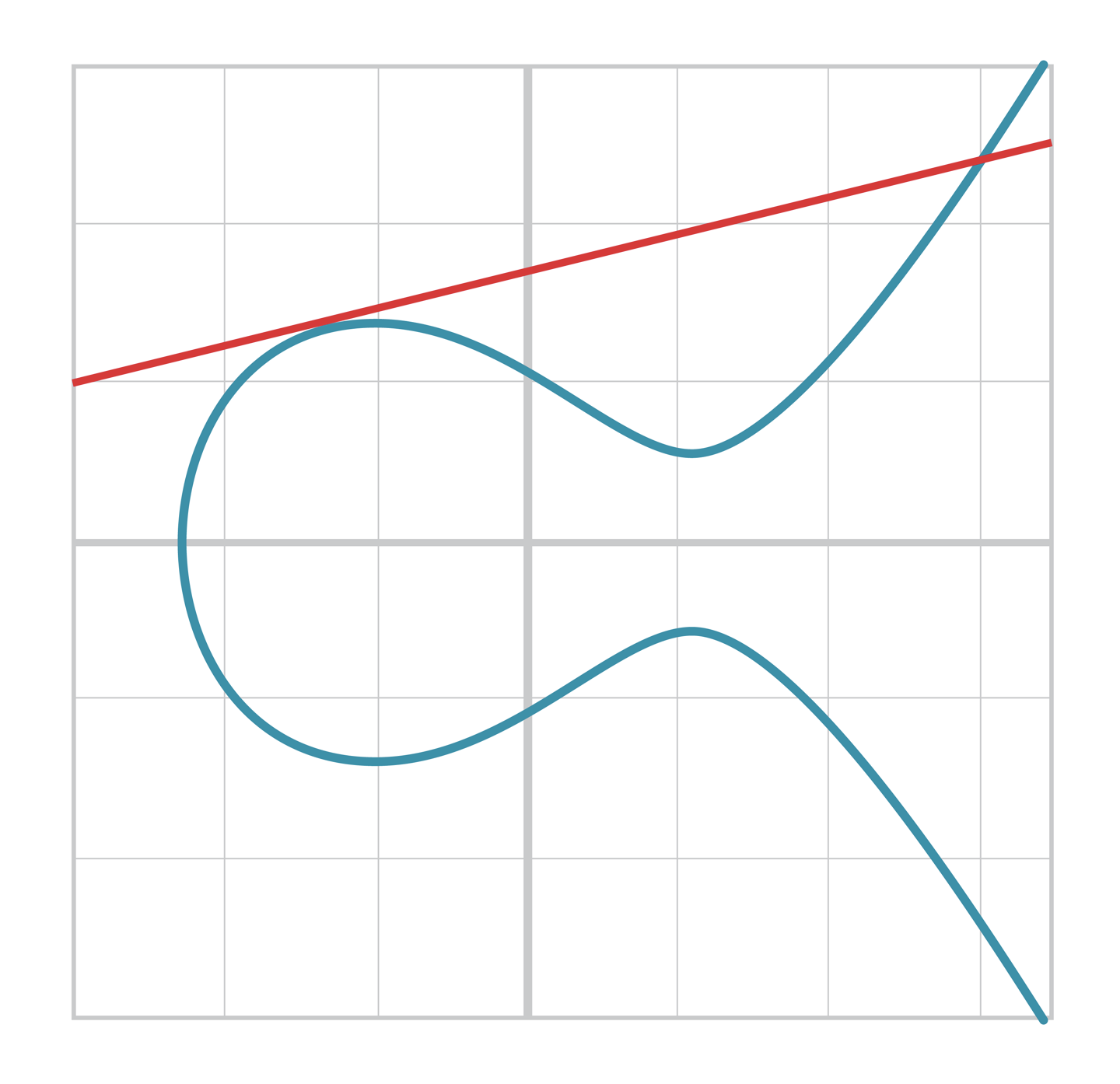
- 이 때의 접선의 기울기를 구하면 다음과 같다.
- 에 대한 공식은 이전 유도 결과에 대입하면 구할 수 있다.
- 그럼 두 점이 같은 경우도 포함하여 메소드를 수정해보자
class Point:
...
def __add__(self,other):
...
if self == other:
s = (3 * self.x**2 + self.a) / (2 * self.y)
x = s**2 - 2 *self.x
y = s * (self.x - x) - self.y2.5.4 예외처리
- 마지막으로 한가지 예외처리 단계가 남았다.
- 접선이 축에 대하여 수직인 경우이다.
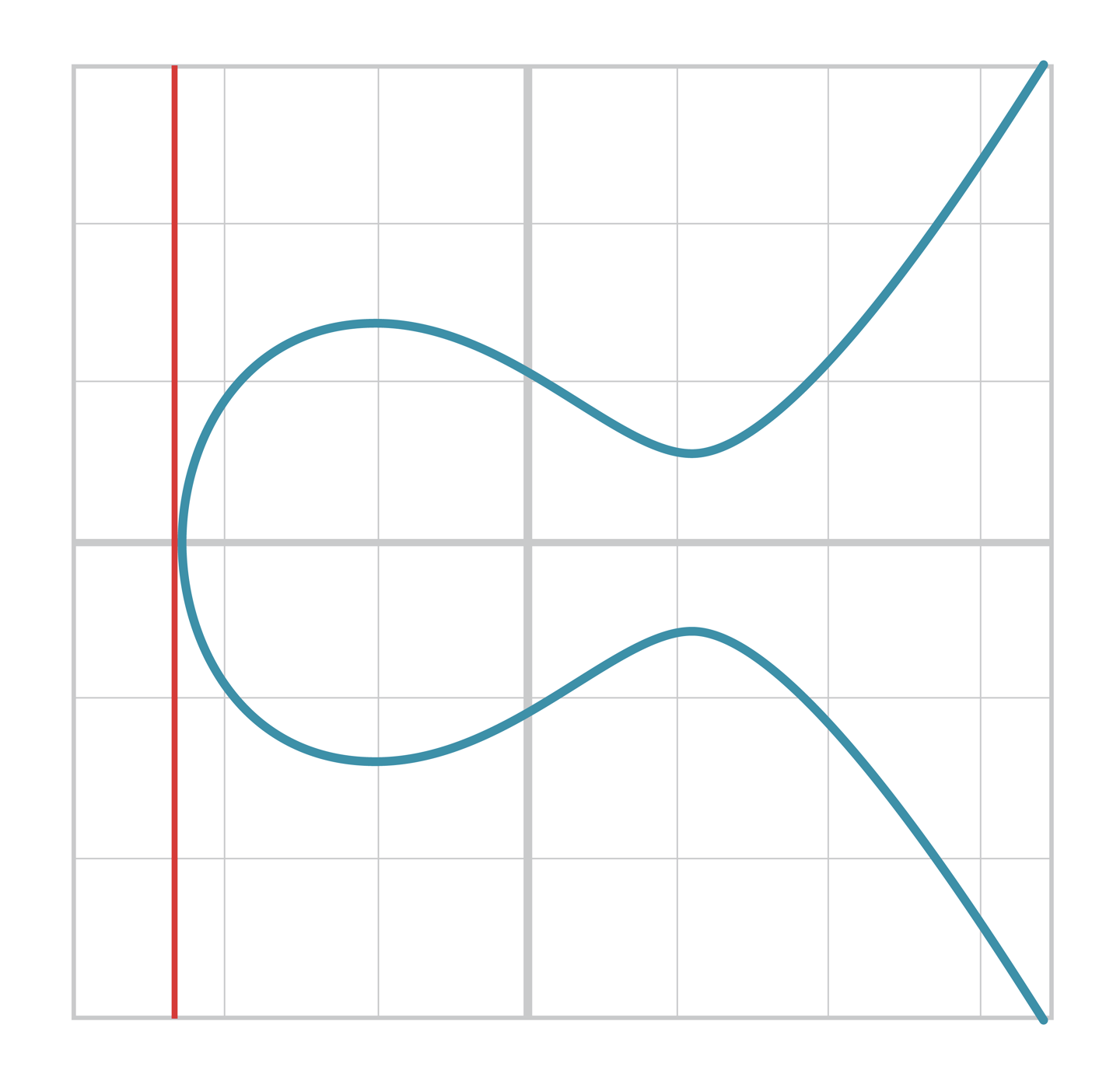
- 위 그림처럼 이면서 동시에 좌표가 인 경우가 존재한다.
- 이 경우에는 분모가 이 되므로 계산 오류가 발생한다.
- 따라서 아래와 같이 예외처리를 해줘야한다.
class Point:
...
def __add__(self,other):
...
if self == other and self.y == -*self.x:
return self.__class__(None, None, self.a, self.b)- 조건문을 통하여 두 점이 같고 좌표가 인 경우 무한 원점을 반환한다.
- *self.y == 0 으로 정의하지 않은 이유는 self.x가 FieldElement 클래스의 객체인 경우 0 * self.x는
클래스에서 정의된 rmul 메소드에 의해 처리되기 때문에 결과는 FieldElement(0,p)가 된다.*
- *self.y == 0 으로 정의하지 않은 이유는 self.x가 FieldElement 클래스의 객체인 경우 0 * self.x는
