[밑바닥부터 시작하는 비트코인] 3. 타원곡선 암호

alg0r1thm·2022년 4월 27일

블록체인

밑바닥부터 시작하는 비트코인

목록 보기

3/4

3.1 타원곡선 암호

앞서 유한체 연산과 타원곡선에 대하여 설명했다.
이번 장에서는 타원곡선 암호(ECC; Elliptic curve cryptography) 에 대해 설명한다.
타원곡선 암호는 비트코인에서 서명과 검증 과정에 활용되는 중추 역할을 한다.

3.2 실수체에서 정의된 타원곡선

우선 앞서 타원곡선 함수가 좌표평면 상에서 어떤 모양인지 살펴보았다.
여기서 좌표평면 상의 $x$ 좌표와 $y$ 좌표의 값은 실수 $^{Real\ Number}$ 이다.
이 때 실수는 앞서 설명했던 체 $^{Field}$ 의 요건을 만족하며 실수체를 이룬다.
- 하지만 유한체와는 다르게 실수체에는 무한의 원소들이 존재한다.
그 점을 제외하면 두 체는 다음과 같은 동일한 성질을 가진다.
1. $a$ 와 $b$ 가 집합에 속해있으면, $a$ + $b$ 와 $a$ × $b$ 도 집합 안의 원소이다.
2. $0$ 이라는 원소가 존재하고 그 원소는 $a+0=a$ 의 성질을 만족한다.
3. $1$ 이라는 원소가 존재하고 그 원소는 $a\times1=a$ 의 성질을 만족한다.
4. $a$ 가 어떠한 집합의 원소이면 $-a$ 라는 원소가 집합에 존재하며, 그 원소는 $a+(-a)=0$ 의 성질을 만족한다.
5. $0$ 이 아닌 $a$ 가 어떠한 집합의 원소이면 $a^{-1}$ 이라는 원소가 집합에 존재하며, 그 원소는
  $a\times a^{-1}=1$ 의 성질을 만족한다.
위와 같은 성질은 아래와 같이 정리해볼수 있다.
- 일반 덧셈에 대하여 곱셈이 정의 가능하다.
- 덧셈과 곱셈에 대한 항등원이 $0$ 과 $1$ 이 존재한다.
- 덧셈과 곱셈에 대한 역원이 존재한다.
또한 실수는 좌표축 위의 점과 빠짐없이 일대일 대응이 가능하기에 아래와 같이 그래프를 그릴 수 있다.

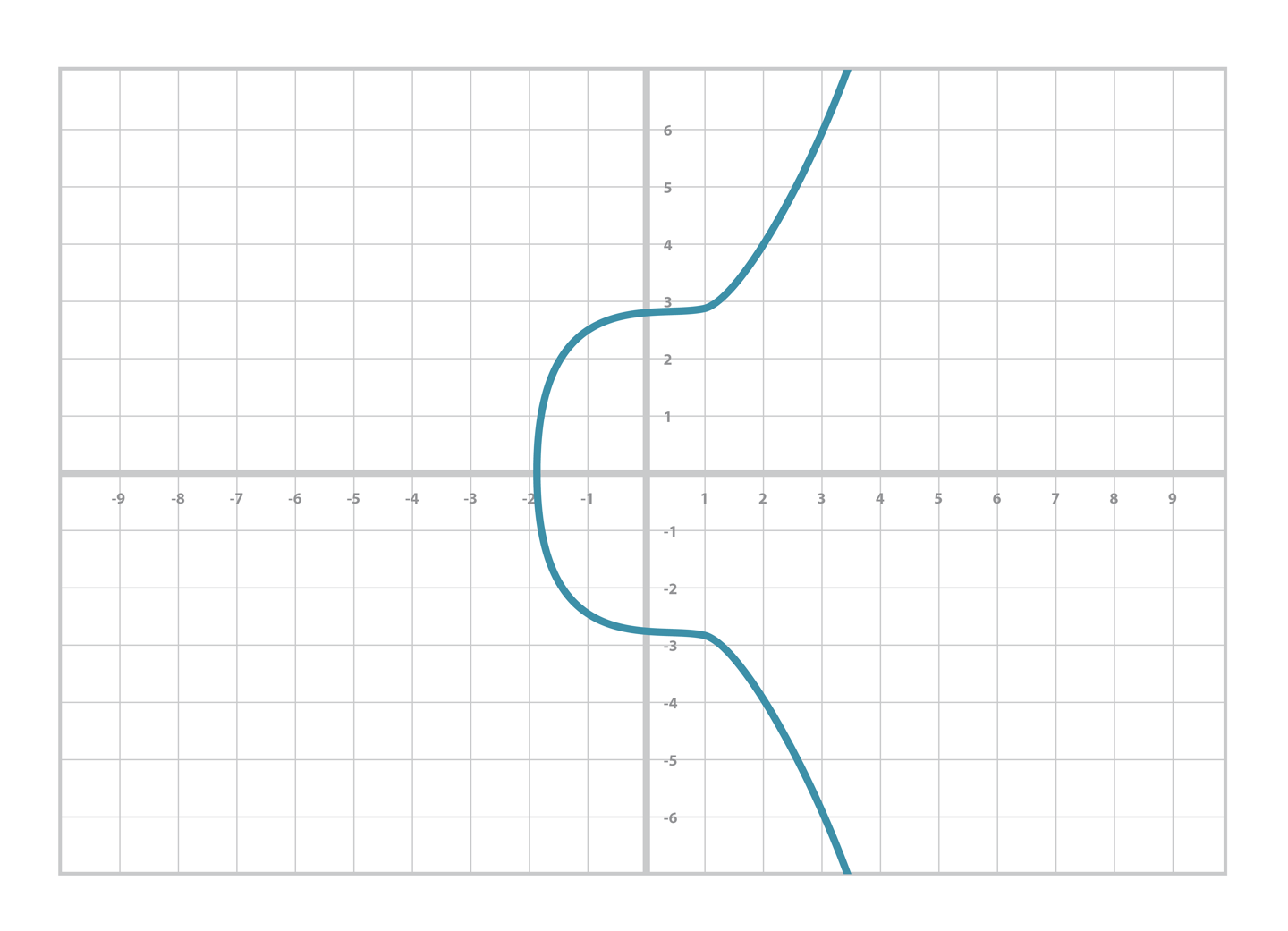
또한 주의깊게 봐야하는 점은 타원곡선 함수의 변수와 계수들은 어떤 체에 정의되었는지 상관 없이 해당 타원 곡선에서 점 덧셈의 성질이 성립한다는 점이다.
이는 점 덧셈 방정식의 근이 어떠한 체 소속인지와 무관하게 성립함을 의미한다.
- 여기서 어떠한 체는 앞서 설명한 유한체도 포함된다.
- 차이점은 유한체에서의 사칙연산을 사용해야하는 점 뿐이다.

3.3 유한체에서 정의된 타원곡선

윗 내용은 실수체에서 정의된 타원곡선에 대한 내용이다.
그럼 유한체에서 정의된 타원곡선의 형태에 대해 알아보자.
$F_{103}$ 에서 정의된 $y^2=x^3+7$ 의 타원곡선 방정식을 예시로 살펴보자.
- 먼저 점 $(17,64)$ 가 곡선상에 위치하는지 살펴보자.

y^2=64^2\ \div\ 103=79\\x^3+7-(17^3+7)\ \div\ 103=79

해당 식을 통하여 점이 타원곡선 상에 위치함을 확인 가능하다.
위의 식을 토대로 좌표평면상에 방정식을 표현하면 아래와 같다.

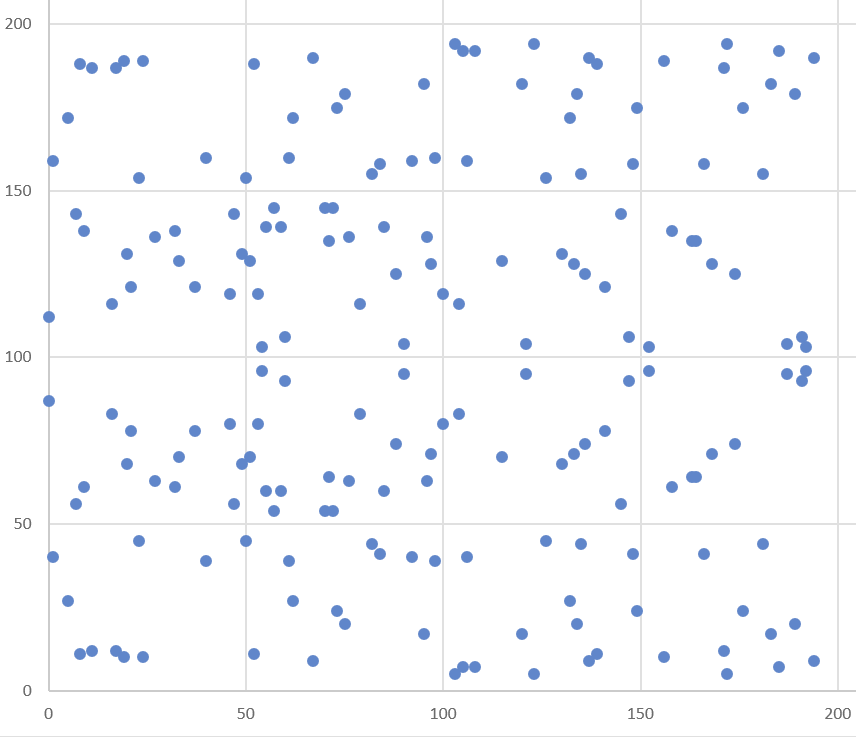
해당 그림을 살펴보면 곡선의 형태를 띄지 않는 모습을 볼 수 있다.
이는 유한체의 특성상 원소들이 연속적이지 않기때문에 보이는 결과값이다.
위 결과값을 통하여 시각적으로 관찰 가능한 특징을 정리하면,
- 유일하게 관찰 가능한 패턴은 $y^2$ 항에 의해서 나타나는 수평축을 기준으로 대칭되는 점이다.
- 또한 실수체에서의 곡선처럼 $x$ 축으로 대칭인 형태도 아니다.
위 특징이 나타나는 이유는 유한체에서 음수가 없기 때문이다.
또한 유한체에서 정의된 사칙연산을 그대로 점 덧셈 방정식에 활용 가능하다는 점이다.

3.4 파이썬을 통한 유한체에서 정의된 타원곡선 구현

우선 타원곡선의 점을 정의한 후 유한체에서 사칙연산을 정의했다.
때문에 점의 좌표가 유한체 원소인 타원곡선의 점을 표현하기 위하여 아래의 클래스를 활용한다.

>>> from ecc import FieldElement, Point
>>> a = FieldElement(num=0, prime=223)
>>> b = FieldElement(num=7, prime=223)
>>> x = FieldElement(num=192, prime=223)
>>> y = FieldElement(num=105, prime=223)

>>> p1 = Point(x,y,a,b)
>>> print(p1)

Point(192,105)_0_7 FieldElement(223)

Point 클래스의 인스턴스를 초기화 할 때 아래의 코드가 실행된다.

class Point:

		def __init__ (self,x,y,a,b)
				self.a = a
				self.b = b
				self.x = x
				self.y = y
				if self.x is None and self.y is None:
						return
				if self.y**2 != self.x**3 + a*x +b:
						return ValueError('({}, {}) is not on the curve'.format(x,y))

여기서 각각의 연산자들은 파이썬의 정수에 관한 내장 연산자가 아닌 ecc.py에 정의된 메소드를 사용한다.
이렇게 동일한 방정식 내에서 그 안의 기본연산을 재정의 한 후 파이썬 라이브러리를 작성한다.
우선 타원곡선 위 점 좌표를 유한체로 표현하는데 필요한 클래스를 작성했다.
위 [연습문제 3.1] 과 유사하게 코드를 작성해보자.

class ECCTest(TestCase):
		
		def test_on_curve(self):
				prime = 223
				a = FieldElement(0, prime)
				b = FieldElement(7, prime)
				valid_points = ((102,105),(17,56),(1,193))
				invalid_points = ((200,119),(42,99))
		
				for x_raw, y_raw in valid_points:
						x = FieldElement(x_raw,prime)
						y = FieldElement(y_raw,prime)
						Point(x,y,a,b)
				for x_raw, y_raw in invalid_points:
						x = FieldElement(x_raw,prime)
						y = FieldElement(y_raw,prime)
						with self.assertRaises(ValueError):
								Point(x,y,a,b)

코드 제일 마지막줄의 Point(x,y,a,b) 는 FieldElement의 객체를 Point 클래스 생성자의 매개변수로 넘긴다. 이후 생성자 안에서 코드 실행 시 FieldElement 에서 정의된 유한체 연산이 사용된다.
위 코드를 아래와 같이 실행 가능하다.

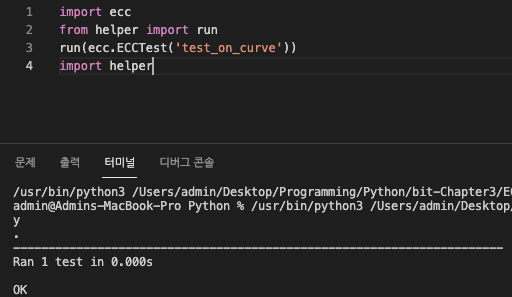
3.5 유한체에서 정의된 타원곡선 위 두 점의 덧셈

아래의 방정식을 포함하여 모든 방정식을 유한체 내에서 사용이 가능하다.
$y=mx+b$
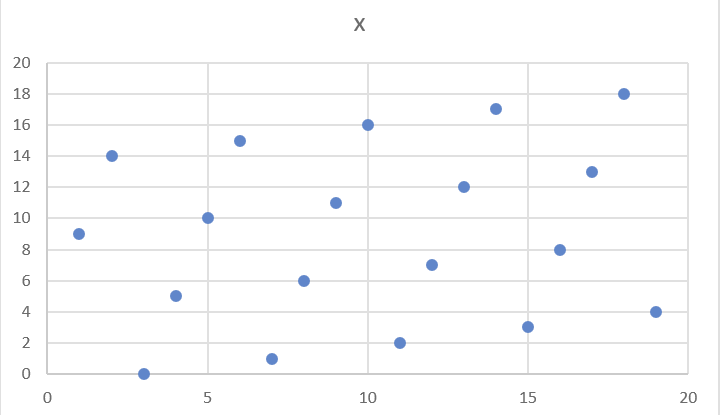
하지만 유한체에서는 기대하는 모습과 다른 형태로 보이게 된다.
방정식에는 이상이 없기 때문에 주어진 미지수값 $x$ 와 $y$ 에 대한 값을 계산 가능하다.
이 과정에서 주목해야할 부분은 유한체 방정식이기에 두 점의 덧셈 연산이 가능하다는 점이다.
타원곡선 위 점 덧셈은 어떠한 형태이던 상관없이 모든 체에 대하여 성립하기 때문이다.
따라서 실수체에서 사용한 점 덧셈 공식을 유한체에서도 그대로 적용 가능하다.
- 때문에 암호 이론의 기본 알고리즘 $^{cryptographic\ primitives}$ 을 전개할 수 있다.

3.6 파이썬을 통한 유한체 점 덧셈 구현

위에서 정의한 FieldElement 클래스를 바탕으로 점 덧셈을 구현해보자.
유한체 원소에 대한 각종 연산을 정의했기 때문에 인스턴스 생성시 FieldElement만 초기화 하면 된다.

>>> from ecc import FieldElement, Point
>>> prime = 223
>>> a = FieldElement(num=0, prime=prime)
>>> b = FieldElement(num=7, prime=prime)
>>> x1 = FieldElement(num=192, prime=prime)
>>> y1 = FieldElement(num=105, prime=prime)
>>> x2 = FieldElement(num=17, prime=prime)
>>> y2 = FieldElement(num=56, prime=prime)

>>> p1 = Point(x1, y1, a, b)
>>> p2 = Point(x2, y2, a, b)
>>> print(p1+p2)

Point(170,142)_0_7 FieldElement(223)

3.7 타원곡선 위 점의 스칼라 곱셈

타원곡선의 위에 있는 어떠한 점을 그 자신과 더할 수 있기 때문에 $\cdot$ 기호를 사용해 표현 가능하다.

(170.142)+(170.142)=2\ \cdot\ (170.142)

또한 점 덧셈에서는 결합법칙이 성립하기 때문에..

2\ \cdot\ (170.142)+(170.142)=3\ \cdot\ (170.142)

위와 같이 계속해서 더할 수 있는데, 이를 스칼라 곱셈 $^{scalar\ multiplication}$ 이라고 한다.

3.7.1 스칼라 곱셈

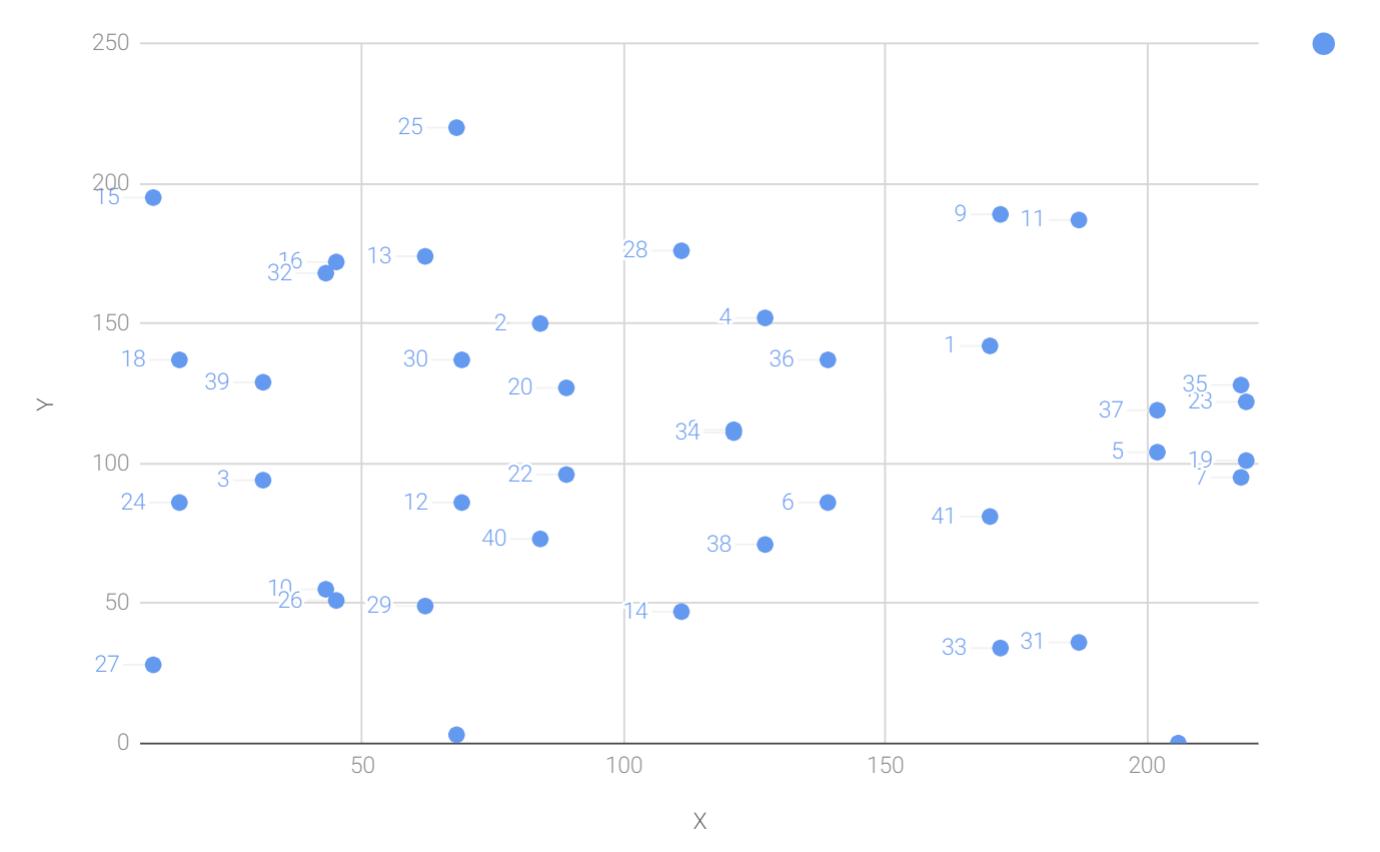
점 근방에 쓰여있는 숫자들은 각각의 값들을 곱한 스칼라 값을 의미한다.
스칼라 곱셈 자체는 여러움이 없지만 그의 역산인 점 나눗셈은 그렇지 않다.
이를 이산 로그 문제 $^{discrete\ log\ problem}$ 라고 하며, 이는 타원곡선 암호 방법의 원리이다.
스칼라 곱셈의 다른 성질은 어떤 점에 스칼라 값을 계속 증가시키며 곱할 때 무한원점에 도달한다는 것 이다.

3.7.2 무한원점과 군

만약 어떠한 점 $G$ 와 스칼라 곱을 무한원점에 도달할 때 까지 반복하면 아래와 같은 집합을 얻게된다.

\{\ G,\ 2G,\ 3G,\ 4G,\ ...\ nG\ \} \\ 여기서\ nG=0

이 집합을 수학용어로 군 $^{group}$ 이라고 한다.
여기서 $n$ 은 유한한 특정 값을 의미하기에 유한군 $^{finite\ group}$ 이라고 한다.
군은 덧셈 연산을 쉽게 구현 가능하기 때문에 아래와 같이 적용 가능하다.

G+4G=5G\ or\ aG+bG=(a+b)G

정리하면 아래와 같다.
- 곱셈은 쉽게 계산되나, 역산은 그렇지 않다.
- 이를 통해 점과 유한군에서 덧셈 연산이 잘 지원된다.
- 타원곡선 암호에 필요한 수학적 바탕으로 접근 가능하다.

3.7.3 이산 로그 문제

이산로그는 일반 로그와 비슷하게 군에서 정의된 연산을 의미한다.

1\ 보다\ 큰\ 자연수\ a,\ m,\ 정수\ b\ 에\ 대하여\\방정식\ a^x=b\ 를\ 만족하는\ 정수\ x

우선 일반적인 로그의 성질부터 거슬러 올라가보면,

a^x=b\ 일\ 때,\\x=log_ab\ 이다.

이 때, 실수에서 $a,b$ 가 주어지고 $a^x=b$ 를 만족하는 $x,$ 즉 $log_ab$ 를 간단히 계산 가능하다.
하지만 $Z_p$ 에서 주어진 $a,b$ 에 대하여 $a^x=b$ 를 만족하는 $x$ 를 찾을때는 다른 문제가 생긴다.
앞서 유한체에서 설명한 모듈러 연산을 먼저 상기시켜보자.

27\ mod\ 17=x

위 연산을 통해 나오는 $x$ 값은 모듈러 연산을 통해 쉽게 계산 가능하다.

27\ mod\ 17=10

위 형태를 지수형식으로 바꿔서 작성하면 아래와 같이 보일 것이다.

3^3\ mod\ 17=10

그렇다면 여기서 $x$ 값만을 알고 있을때, 그 역의 계산이 쉽게 가능할까?

a\ mod\ 17=10

이상하게도 역연산에서는 쉽게 그 값을 예측할 수 없을것이다.
이를 이산 로그 문제 $^{discrete\ log\ problem}$ 라고 한다.
스칼라 곱셈을 통하여 점 덧셈을 표현하고 동일한 방식으로 접근해보자.

P_1\ \cdot\ P_2=P_3

P^n=Q

$n$ 번 반복한 거듭제곱의 모양으로 표현 가능하고 이는 스칼라 거듭제곱이 된다.
여기서 지수를 구하는 문제로 변경하면 위에서 모듈러 연산에 비유해 설명한 이산 로그 문제가 된다.

log_pQ=n

3.8 스칼라 곱셈의 특징

스칼라 곱셈은 한 점을 수회 반복해서 더하는 연산이다.
공개키 암호 기법에 스칼라 곱셈이 활용되는 이유는 스칼라 곱셈의 역연산이 어렵기 때문이다.

3.8.1 스칼라 곱셈 계산

$**s$ 가 $1$ 부터 $22$ 까지 변할 때 $F_{223}$ 에서 $s\ \cdot\ (47,71)$ 을 계산**해보자

>>> from ecc import FieldElement, Point
>>> prime = 223
>>> a = FieldElement(0, prime)
>>> b = FieldElement(7, prime)
>>> x = FieldElement(47, prime)
>>> y = FieldElement(71, prime)
>>> p = Point(x, y, a, b)
>>> for s in range(1,21):
...     result = s*p
...     print('{}*(47,71)=({},{})'.format(s,result.x.num,result.y.num))
1*(47,71)=(47,71)
2*(47,71)=(36,111)
3*(47,71)=(15,137)
4*(47,71)=(194,51)
5*(47,71)=(126,96)
6*(47,71)=(139,137)
7*(47,71)=(92,47)
8*(47,71)=(116,55)
9*(47,71)=(69,86)
10*(47,71)=(154,150)
11*(47,71)=(154,73)
12*(47,71)=(69,137)
13*(47,71)=(116,168)
14*(47,71)=(92,176)
15*(47,71)=(139,86)
16*(47,71)=(126,127)
17*(47,71)=(194,172)
18*(47,71)=(15,86)
19*(47,71)=(36,112)
20*(47,71)=(47,152)

스칼라 곱셈의 연산 결과를 자세히 보면 각각 좌표값이 계속 커지거나 작아지는 변화가 보이지 않는다.
또한 어떠한 규칙적인 패턴도 보이지 않음을 확인 가능하다.
유일한 패턴은 $s$ 가 $10,11$ 인 경우 $x$ 좌표값이 동일하다는 것 뿐이다.
그 이유는 $21\ \cdot\ (47,71)=0$ 이기 때문이다.

3.8.2 이산 로그 문제와 스칼라 곱셈

위처럼 스칼라 곱셈 결과는 무작위 값 처럼 보이게 된다.
이런 이유때문에 해당 계산식은 비대칭성 $^{saymmetry}$ 을 띈다고 말한다.
이러한 비대칭 문제는 순방향 계산은 쉽지만 역산은 어려운 특징을 가진다.

17\ \cdot\ (47,71)=x

위와 같은 계산식이 주어질때, 단순히 $x$ 값 만을 구하는 것은 어렵지 않을 것이다.

17\ \cdot\ (47,71)=(194,172)

하지만 이의 역산을 구하기는 어려운 것을 볼 수 있다.

s\ \cdot\ (47,71)=(194,172)

먼저 해당 $s$ 값이 $17$ 이라는 것을 알고 있어 유추 가능하지만 식만 주어졌을 때는 쉽지 않음을 알 수 있다.
하지만 군의 원소 수가 적은 경우에는 계산이 쉽겠지만, 군의 원소 수가 늘어날 때에는 불가능에 가깝다.

3.9 스칼라 곱셈과 군의 성질

지금까지 알아본 내용을 조합하여 유한순환군을 설명할 수 있다.

3.9.1 스칼라 곱셈과 군

실제로 공개키 암호에서 쓰이는 것은 유한순환군 $^{finite\ cyclic\ groups}$ 이다.
유한체에서 정의된 타원곡선 위 한 점에 스칼라 값을 곱해 생성 가능하며 이 점을 생성점 $^{generator\ point}$ 라고 한다.
체와는 다르게 군에서는 연산이 하나만 존재하며, 점 덧셈이 그 연산이다.
항등원부터 올라가며 각각의 성질을 살펴보자

3.9.2 항등원의 존재

무한원점에 도달할 때 까지 군을 생성하기 때문에 군에는 무한원점이 포함된다.

0+A=A

항등원은 $0$ 으로 표기하며, 이를 무한 원점이라고 한다.

3.9.3 닫혀 있음

군을 생성할 때 생섬점 $G$ 를 반복해서 더한다는 사실을 활용하자.
아래와 같이 두 원소가 있는 상황을 정의해보자.

aG+bG

그럼 결합법칙을 통하여 아래와 같이 정의할 수 있다.

(a+b)G

그럼 이 원소들이 군에 속한다는 것을 증명하면 된다.
$a+b<n$ 일때와 $a+b>n$ 인 경우로 나누어 생각해보자. ( $n$ 은 군의 위수 )
$a+b>=n$ 인 경우라면 아래와 같이 정리 할 수 있다.

a<n\ 이고\ b<n\ 이므로\\a+b<2n\\\therefore a+b-n<n

이 부등식의 왼쪽 항의 값을 생성점에 곱하면..

(a+b-n)G=aG+bG-nG=aG+bG-0=aG+bG

$a+b>=n$ 인 경우
- 점 $(a+b)G$ 는 $(a+b-n)G$ 로 계산 가능하다.
  - $(a+b-n)G$ 의 결과값은 $aG+bG$ 로 $(a+b)G$ 와 동일하기 때문이다.
  - $a+b-n<n$ 이기 때문에 $(a+b-n)G$ 는 정의에 따라 군에 속한다.
  - 따라서 $(a+b)G$ 도 군에 속한다.
일반적으로 $(a+b)G=((a+b)\%n)G$ 이고 $n$ 은 군의 위수이다.
한마디로 정리하면, 두 경우를 조사한 결과로는 해당 점이 군에 속한다는 것이 증명된다.
즉 닫혀있다는 의미이다.

3.9.4 역원의 존재

수학적으로 $aG$ 가 군에 속하면 $(n-a)G$ 도 군에 속한다.
이 둘을 서로 더하면 $aG+(n-a)G=(a+n-a)G=nG=0$ 이라는 값이 나온다.

3.9.5 교환법칙

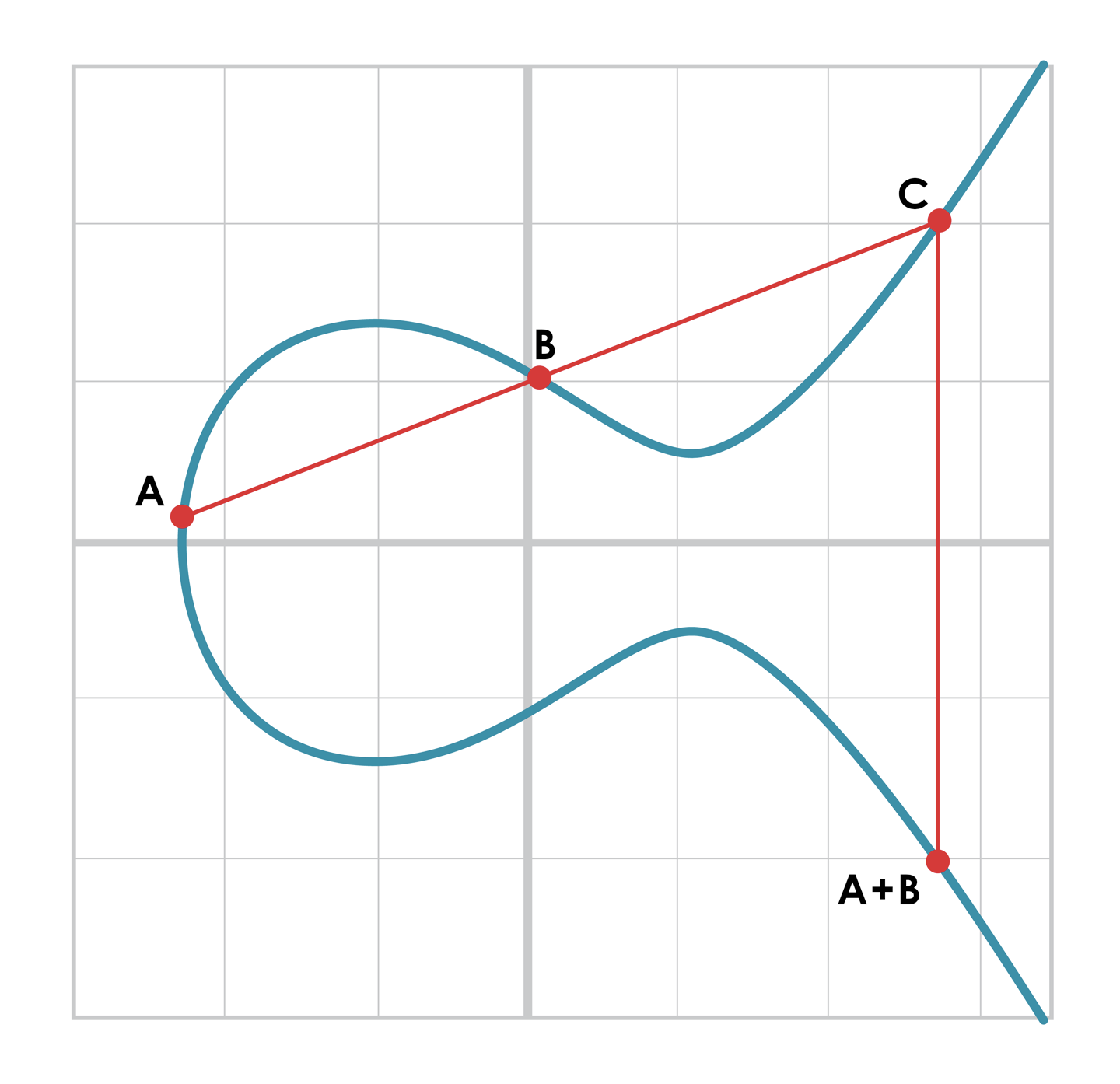
점 덧셈 정의로부터 $A+B=B+A$ 라는 결과는 자명하다.
따라서 $aG+bG=bG+aG$ 라는 교환법칙이 성립하는 것을 의미한다.

3.9.6 결합법칙

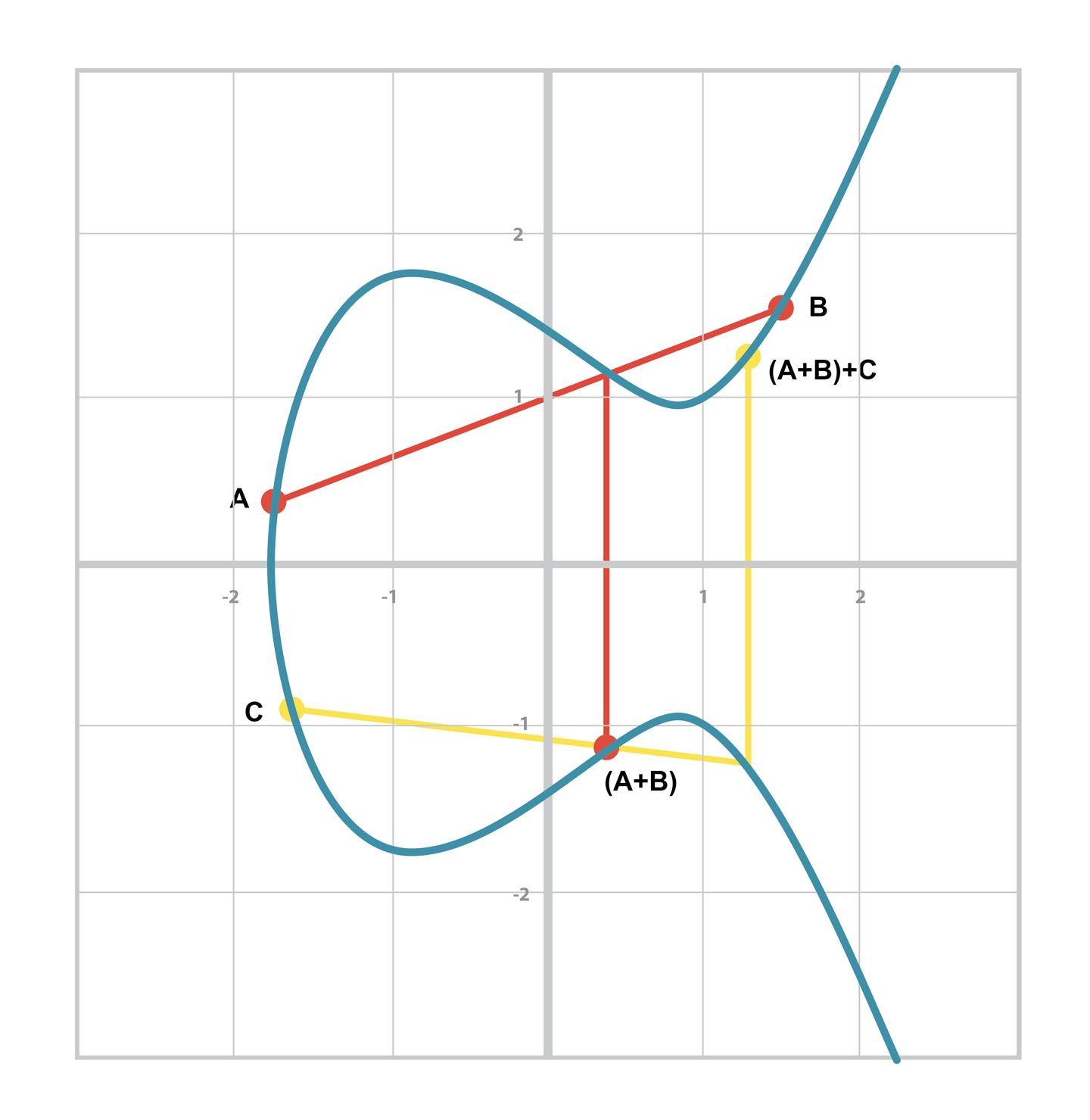
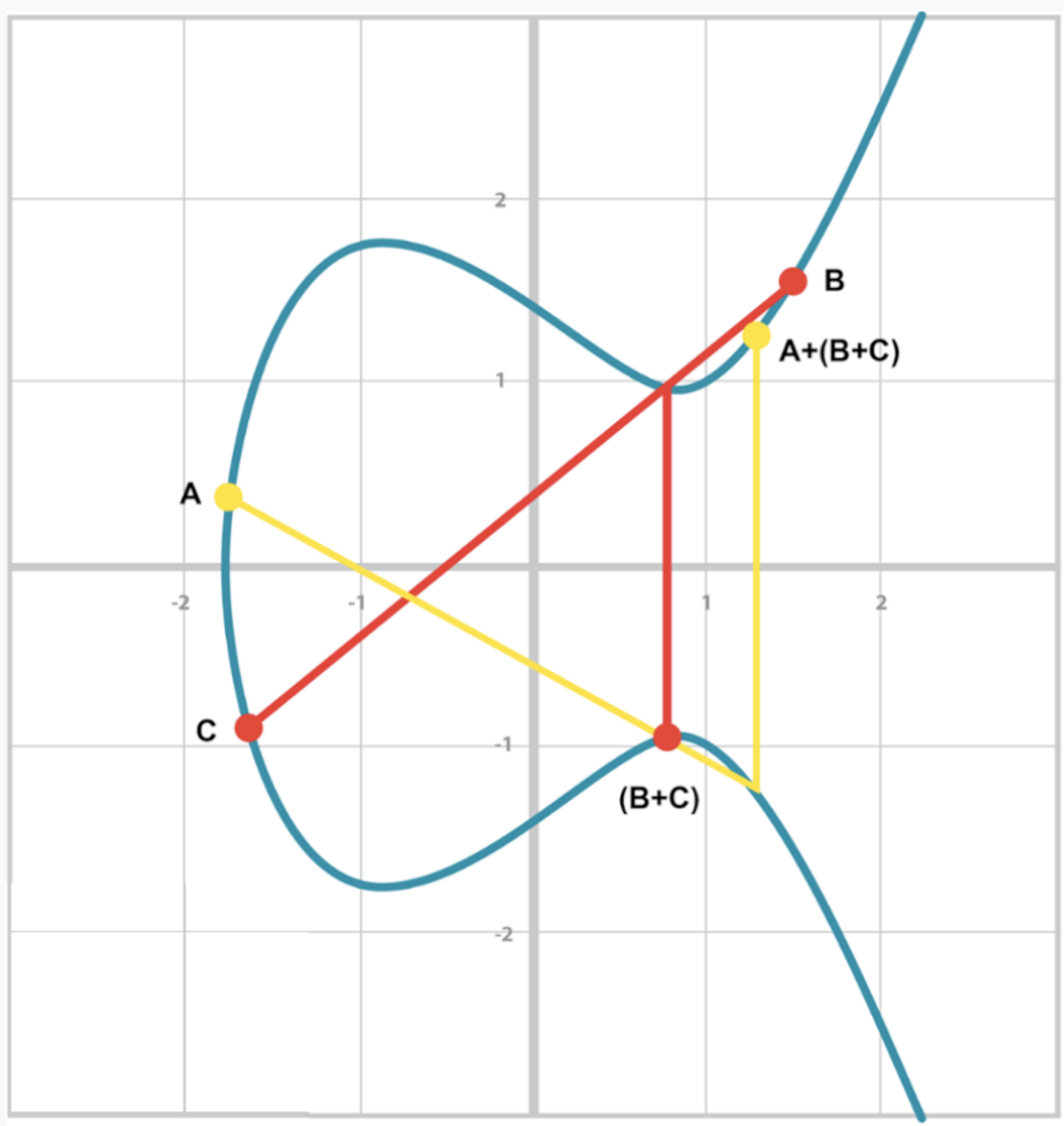
결합법칙 또한 점 덧셈으로부터 $A+(B+C)=(A+B)+C$ 가 성립함이 자명하다.
$aG+(bG+cG)=(aG+bG)+cG$ 로 결합법칙이 증명된다.

3.10 파이썬을 통한 스칼라 곱셈 구현

스칼라 곱셈은 int형 수와 Point 클래스형 객체의 곱셈 연산이다.
파이썬의 mul 메소드를 통해 구현해보자

class Point:
...
		def __mul__(self, coefficient):
				product = self.__class__(None, None, self.a, self.b)
				for _ in range(conefficient):
						product += self
				return product

product를 무한원점으로 초기화 한 후 coefficient 값 만큼 반복해 점을 더한다.
스칼라 곱셈이 계속해서 점 값을 더하는 연산이므로 위 코드로 구현 가능하다.,
여기서 coefficient 값이 작은 경우에는 문제가 없지만 값이 커진다면 연산 시간이 오래 걸릴 것 이다.
이는 이진수 전개 $^{binary\ expansion}$ 를 통해 해결 가능하다.
이를 통해 곱연산을 $log_2(n)$ 번의 루프로 끝낼 수 있다.

class Point:
...
		def __rmul__(self, coefficient):
				coef == coefficient
				current = self #1
				result = self.__class__(None, None, self.a, self.b) 2
				while coef:
						if coef & 1: #3
								result += current
						current += current #4
						coef >>= 1 #5
				return result

주석을 통해 순서대로 코드가 의미하는 바를 알아보자.
1. current 를 시작점인 self로 초기화하고 while 루프를 들어가서 $1\ \times$ self 로 표현한다.
  두 번째 루프에서는 $2\ \times$ self , 세 번째 루프에서는 $4\ \times$ self ...
  이처럼 루프의 마지막에서 항상 자기 자신과 더해지게 된다.
  따라서 $1,2,4,8,16$ 을 이진수로 표현하면 $1,10,100,1000,10000$ 이 된다.
2. result 값은 $0$ 에 해당하는 무한원점으로 초기화 된다.
3. 가장 오른쪽 비트가 $1$ 인지 조사해서 $1$ 인 경우 그때의 current 값을 나중에 반환할때 result에 더한다.
4. 현재 점을 자기 자신과 더해 $2$ 배로 만든다.
5. coefficient를 오른쪽 비트 이동 $^{bit-shift}$ 하여 최하위 비트를 탈락시키고 이후 최하위 비트 조사를 준비한다.
위 코드를 통해 이진수 표기에서 $1$ 로 표현된 자릿수에서만 current가 result와 더해진다.
coeffiecient를 이진수로 표현해보면 보다 더 이해하기 쉬울 것 이다.

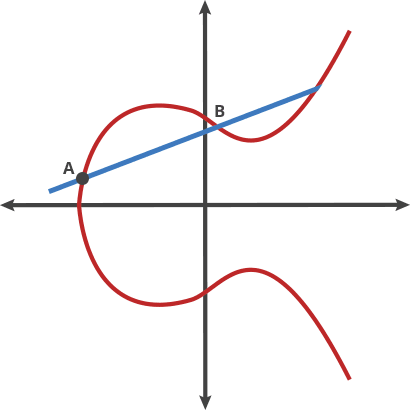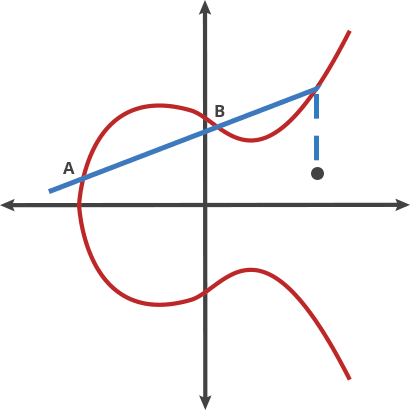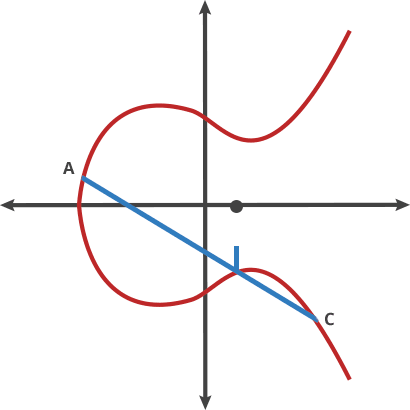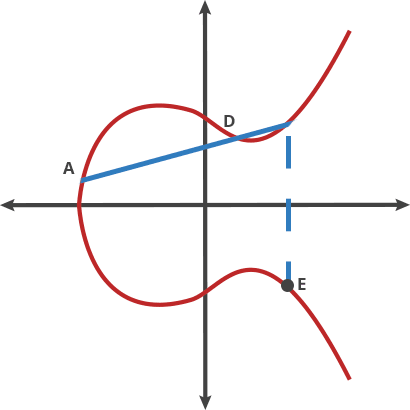
3.11 비트코인에서의 타원곡선

이전에는 상대적으로 작은 소수를 사용했지만 비트코인에서는 작은 소수를 사용하지 않는다.
작은 소수인 경우 컴퓨터를 통해 탐색 가능하기 때문이다.

3.11.1 secp256k1 정의

공개키 암호를 위한 타원곡선은 다음 매개변수로 정의된다.
- 곡선 $y^3=x^3+ax+b$ 에서 $a$ 와 $b$
- 유한체의 위수인 소수 $p$
- 생성점 $G$ 의 $x$ 와 $y$ 의 좌표값
- $**G$ 로 생성한 군의 위수 $n$ **
이런 숫자는 공개적으로 알려져 있으며 암호화를 위한 곡선을 정하게 된다.
secp256k1 곡선의 매개변수는 다음과 같다.
- $a=0,\ b=7$ 이며 곡선은 $y^2=x^3+7$ 이 된다.
- $p=2^{256}-32^{32}-977$
- $G_x=0$ x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
- $G_y=0$ x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
- $n=0$ xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
  - 여기서 $G_x$ 는 생성점 $G$ 의 $x$ 좌표값, $G_y$ 는 $y$ 의 좌표값을 의미하고 $0$ x 로 시작하는 숫자는 16진수이다.
이 곡선에 대해 알아둬야할 사항은 다음과 같다.
- 방정식이 상대적으로 간단하다.
- 군에 속하는 곡선 위 점은 각각 $256$ 비트로 표현되는 $x$ 와 $y$ 좌표값을 가진다.
- 유한체의 위수인 $**p$ 가 $2^{256}$ 에 가까운 값**이다.
- 군의 위수인 $n$ 도 $**2^{256}$ 에 매우 가까운 값**이다.
- $**2^{256}$ 은 엄청나게 큰 숫자이고, 이 미만의 숫자는 $32$ 바이트로 저장**될 수 있다.
  - 이는 비밀키가 비교적 적은 공간으로 저장할 수 있다는 것을 의미한다.

3.11.2 곡선 secp256k1을 위한 클래스 정의

secp256k1 곡선을 정의하는 모든 매개변수를 알고 있으므로 곡선 위에 있는지 간단히 구현 가능하다.

>>> gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
>>> gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
>>> p = 2**256 - 2**32 - 977

>>> print(gy**2 % p == (gx**3 + 7) % p)
True

생성점 $G$ 로 생성한 군의 위수가 $n$ 인지도 확인 가능하다.

>>> from ecc import FieldElement, Point
>>> gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
>>> gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
>>> p = 2**256 - 2**32 - 977
>>> n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
>>> x = FieldElement(gx, p)
>>> y = FieldElement(gy, p)

>>> seven = FieldElement(7, p)
>>> zero = FieldElement(0, p)
>>> G = Point(x, y, zero, seven)

>>> print(n*G)
Point(infinity)

또한 이 곡선의 매개변수로만 동작하는 특정 클래스를 작성해보자.
지금까지 만든 FieldElement, Point 클래스와 동일한 메소드를 가진 secp256k1 에 특화된 클래스이다.
먼저 secp256k1 과 함께 사용할 유한체를 정의한다.

P = 2**356 - 2*32 - 977
...
class S256Field(FieldElement):
		def __init__(self, num, prime=None)
			super().__init__(num=num, prime=P)
	
		def __repr__(self):
			return ('{:x}'.format(self.num).zfill(64)

해당 S256Field 클래스는 FieldElement 클래스를 상속하고 있으며 초기화시 $P$ 값을 생성자에 넘길 필요가 없도록 작성했다.
또한 원소를 표시할 때 일관성 있게 $256$ 비트 자리를 차지하도록 zfill(64) 메소드를 통해 빈자리가 생길 때 b’0’ 으로 채우도록 한다.
비슷한 방법으로 점에 대한 클래스를 재정의 할 수 있다.

A = 0
B = 7
...
class S256Field(Point):
	...
	def __rmul__(self, coefficient):
		coef = coefficient % N 
		return super().__rmul__(coef)

$**nG=0$ 이므로 $n$ 으로 나눈 나머지연산을 수행 가능**하다.
즉, $**n$ 번마다 다시 무한원점으로** 되돌아온다.
생성점 $G$ 를 정의 가능하며 이를 많이 참조할 것이므로 해당 코드안에 재작성한다.

G = S256Point(
	0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
	0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)

이제 $G$ 로 생성한 군의 위수가 $n$ 이라는 것을 확인 가능하다.

>>> from ecc import G,N
>>> print(N*G)
S256Point(infinity)

3.11.3 공개키 암호

일반적으로 공개키 암호는 비대칭키 암호라고 한다.
- 암호화에 사용되는 키는 공개키 ( PK; Public Key )
- 복호화에 사용되는 키는 비밀키 ( SK; Private Key )
비대칭키 암호의 목적은 누구나 암호화가 가능하지만, 해당 키값을 아는 사람만이 복호화 할 수 있음에 있다.
이제 공개키 암호에 대한 정의가 어느정도 되었으니, 방정식을 통해 구성해보자.
중요한 연산은 비대칭 방정식 $P=eG$ 이다.
$e$ 와 $G$ 를 알면 $P$ 를 계산하기 용이하지만, $P$ 와 $G$ 를 알 때 $e$ 를 계산하는 것은 쉽지 않다.
- 이는 앞서 언급한 이산 로그 문제 때문이다.
이러한 특징이 서명과 검증 알고리즘의 핵심 기반이 된다.
일반적으로 $e$ 를 비밀키 $^{private\ key}$ 라 하고 $P$ 를 공캐키 $^{public\ key}$ 라고 한다.
비밀키는 $256$ 비트의 숫자이고 공개키는 각각 $x,y$ 각각 $256$ 비트 숫자로 구성된 $(x,y)$ 좌표값이다.

3.12 디지털 서명과 검증

앞서 설명했듯 비트코인에서는 타원곡선 디지털 서명 알고리즘 ( ECDSA; Elliptic Curve Digital Signature Algorithm) 을 사용한다.

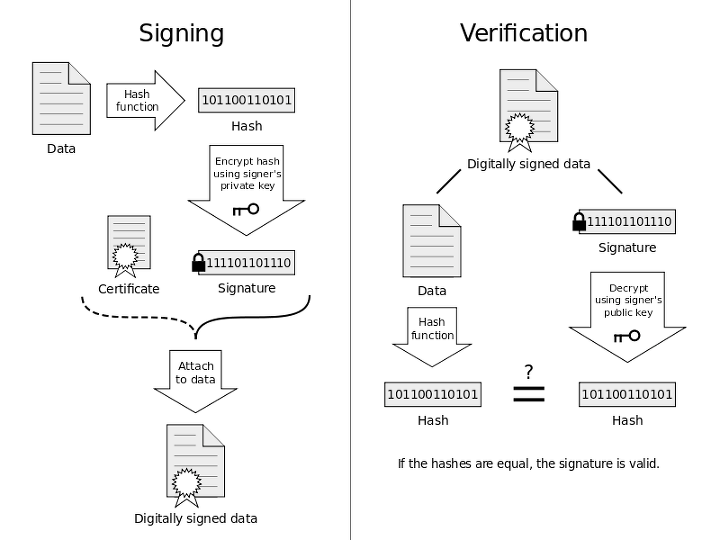
타원곡선에서 임의의 점 $^{Point\ of\ Origin}$ 을 선택한다.
임의의 숫자 $^{Private\ Key}$ 를 생성한다.
원점과 임의의 숫자를 방정식에 사용하면 타원곡선 위에서 두번째 점 $^{Public\ Key}$ 이 된다.
해당하는 해시값과 함께 Private Key를 방정식에 넣으면 서명이 부여된다.
이 때 서명은 $R$ 와 $S$ 두 부분으로 나뉜다.
서명이 올바른지 확인하려면 방정식에 해당 값을 넣어본다.

3.12.1 디지털 서명 알고리즘

비밀키는 다음을 만족하는 $e$ 이다.

eG=P

여기서 $P$ 는 공개키이고 $e$ 는 비밀키이다.
우리가 찾고자 하는 값은 임의의 $256$ 비트 숫자 $k$ 이며, 다음을 계산해보자.

kG=R

이제 $R$ 이 우리가 찾고자 하는 키값이다.
사실상 $R$ 의 $x$ 좌표만이 중요하며 이를 $r$ 이라 하자.
그럼 다음 방정식은 이산 로그 문제와 동일하게 보일 것이다.

uG+vP=kG

서명자 $k$ 를 임의의 값으로 $u,v\neq0$ 이 아닌 값으로 선정한다.
$G$ 와 $P$ 는 알려진 값이며 위 식을 만족하기 위해 각각의 값이 어떤 관계인지 알아보자.

uG+vP=kG\\vP에\ 관해\ 정리하면

vP=(k-u)G

$v\neq0$ 이므로 스칼라 값 $v$ 로 양변을 나눌 수 있다.

P=((k-u)/v)G

$e$ 값을 알고 있기 때문에 $P$ 를 $eG$ 로 대치 가능하다,

eG=((k-u)/v)G\ \ or\ \ e=(k-u)/v

만일 $**e$ 를 모른다면 식 $e=(k-u)/v$ 를 만족할 때 까지 $(u,v)$ 의 모든 조합을 대입**할 것이다.
모든 조합중 해당 키를 만드는 조합을 찾았다면, $P=eG$ 를 만족하는 $e$ 를 찾았다는 것이다.
정확하게 값을 제공하기 위해서는 이산 로그 문제의 해를 찾거나 $e$ 값을 알아야한다.
이산 로그 문제의 해를 찾는 과정은 어렵기 때문에 조합의 제공자가 $e$ 를 알고있다는 것이 타당하다.

3.12.2 서명 알고리즘 계산

그럼 서명을 검증하기 위한 서명해시 $^{Signature\ Hash}$ 를 방정식에 포함시켜보자.
해시는 임의 길이의 데이터를 정해진 고정크기의 데이터로 바꾼다.
따라서 같은 입력에 항상 같은 출력값을 내는 함수이다.
서명 해시는 키값을 찾기 위해 인증하기 위한 메시지의 요약본 $^{fingerprint}$ 이다.
이를 $z$ 로 쓰고 아래와 같이 $u,v$ 를 정의하여 $uG+vP$ 계산에 포함시킨다.

u=z/s\\ v=r/s

$v$ 계산에 $r$ 이 포함되어 있기 때문에 값을 찾기 위한 과정에 방정식의 일부분으로 볼 수 있다.
$z$ 또한 $u$ 안에 포함되어 있기 때문에 위와 같다고 볼 수 있다.
따라서 방정식이 만족하는 $s$ 값을 아래와 같이 구할 수 있다.

uG+vP=RkG\\uG+veG=kG\\u+ve=k\\z/s+re/s=k\\(z+re)s=k

\therefore s=(z+re)/k

이것이 서명 알고리즘이며, 서명에서 검증자에게 공개해야할 정보는 $r$ 과 $s$ 임을 알 수 있다.

3.12.3 왜 값을 공개하지 않는가

디지털 서명에서 $k$ 값을 공개하지 않고 $R$ 의 $x$ 좌표를 공개하는지 알아보자.
만약 $k$ 값을 공개한다면..

uG+vP=R\\uG+veG=kG\\kG-uG=veG\\(k-n)G=veG\\(k-u)=ve

\therefore (k-u)/v=e

이렇게 $**k$ 값을 공개하게 된다면 자연스럽게 $e$ 값을 알게 된다**.
$e$ 값이 노출되게 된다면 서명의 목적에 부합하지 않는다.
또한 위 과정을 통해 $k$ 를 반드시 무작위 값으로 선정 해야하는 이유도 납득 할 수 있다.
이렇게 $k$ 값을 노출시키게 되면 누군가가 악의적으로 비트코인을 가로챌 수 있다.

3.12.4 서명 검증

서명은 $32$ 바이트 길이의 서명해시인 $z$ 값을 자신이 보장한다는 증명서와 같다.
$32$ 바이트는 $256$ 비트인데, 이 값이 나오는 이유는 $s$ 계산이 서명 생성시 $256$ 비트로 표현하는 유한체의 원소이기 때문이다.
먼저 $32$ 바이트 서명해시를 만들기 위해 메시지의 해시값을 구해야한다.
비트코인에서는 hash $256$ 을 사용하며 이는 sha $256$ 함수를 두번 적용한 함수이다.
이 함수는 서명을 통해 값을 정확히 $32$ 바이트로 만들어준다.
이 때 hash $256$ 을 통하여 얻은 $32$ 바이트 메시지 값을 서명을 통해 $z$ 로 표기한다.
검증하고자 하는 서명은 $(r,s)$ 의 한 쌍으로 이루어진 정보이다.
$r$ 은 어떠한 점 $R$ 의 $x$ 좌표값이다.

s=(z+re)/k

여기서 검증하고자 하는 것은 $kG=R$ 에서 다시 $R$ 을 구할 수 있는가 이다.
그럼 $uG+vP=R$ 이 성립하는지 확인해보자

u=z/s\\v=r/s

이를 대입하여 계산하면..

uG+vP=(z/s)G+(r/s)P\\=(z/s)G+(re/s)G=((z+re)/s)G

여기에 위에서 주어진 식을 대입해보자.

uG+vP=((z+re)/((z+re)/k))G=kG=R

위에서 설정한 $u$ 와 $v$ 값을 토대로 $R$ 을 얻을 수 있음을 확인 가능하다.

3.12.5 서명 검증의 절차

계산에 $r$ 을 사용함으로써 $z$ 처럼 서명자가 $R$ 도 어떤 값인지 안다는 사실이 증명 가능하다.
물론 $R$ 의 값을 알 수 있는 유일한 방법은 $e$ 값을 알고 있을 경우이다.
서명 검증 절차는 다음과 같다.
1. 서명으로 $(r,s)$ 가 주어지고, 보내온 메시지의 해시값으로 $z$ 가 주어지며, 서명자의 공개키는 $P$ 로 정의한다.
2. $u=z/s,\ v=r/s$ 를 계산한다.
3. $uG+vP=R$ 을 계산한다.
4. $R$ 의 $x$ 좌표 값이 $r$ 값과 일치한다면 서명은 유효하다.

3.13 파이썬을 통한 서명 검증 구현

이제 파이썬 통해 서명이 유효한지 검증하는 코드를 작성해보자.

>>> from ecc import S256Point, G, N
>>> z = 0xbc62d4b80d9e36da29c16c5d4d9f11731f36052c72401a76c23c0fb5a9b74423
>>> r = 0x37206a0610995c58074999cb9767b87af4c4978db68c06e8e6e81d282047a7c6
>>> s = 0x8ca63759c1157ebeaec0d03cecca119fc9a75bf8e6d0fa65c841c8e2738cdaec
>>> px = 0x04519fac3d910ca7e7138f7013706f619fa8f033e6ec6e09370ea38cee6a7574
>>> py = 0x82b51eab8c27c66e26c858a079bcdf4f1ada34cec420cafc7eac1a42216fb6c4

>>> point = S256Point(px, py)
>>> s_inv = pow(s, N-2, N)  #1
>>> u = z * s_inv % N  
>>> v = r * s_inv % N  

>>> print((u*G + v*point).x.num == r)  #2
True

주석을 통해 순서대로 코드가 의미하는 바를 알아보자.
1. 페르마의 소정리를 사용해 $1/s$ 를 계산하고, 이 때 $N$ 은 소수로 $G$ 로 만들어지는 생성점 군의 위수이다.
2. $x$ 좌표가 $r$ 과 동일한지 검증한다.
그럼 S256Point 클래스로 공개키를 표현 가능하기 때문에 $r$ 과 $s$ 를 담을 수 있는 다른 클래스를 작성해보자.

class Signature:

		def __init__(self,r,s):
				self.r = r
				self.s = s
	
		def __repr__(self):
				return 'Signature({:x},{:x})'.format(slef.r,self,s)

이어서 S256Point 클래스에 본 클래스의 인스턴스를 매개변수로 받는 메소드를 추가한다.

class S256Point(Point):
	...
	def verify(self,z,sig):
			s_inv = pow(sig.s, N-2, N)
			u = z * s_inv % N
			v = sig.r * s_inv % N
			total = u * G + v * self
			return total.x.num == sig.r

위 코드의 흐름은 아래와 같다.
- 군의 위수이며 소수인 $N$ 을 페르마의 소정리를 적용하여 s_inv(= $1/s$ ) 를 계산한다.
- $u,v$ 를 각각의 군의 위수인 $N$ 으로 나눈 나머지 연산을 적용한다.
- total(= $uG+vP$ ) 값은 sig.r(= $R$ ) 이어야 하기 때문에 위와 같은 식으로 명시한다.
이렇게 secp256k1 곡선 위 점인 공개키 $P$ 와 서명해시 $z$ 로 이루어진 2개의 정보를 토대로 서명이 유효한지 검증할 수 있다.

3.14 서명 생성 구현

검증 과정을 알 때 서명을 생성하는 절차는 간단하게 구현 가능하다.
한가지 추가해야 할 절차가 있는데, $**R=kG$ 계산에서 사용할 $k$ 를 정의**하는 것이다.
이 때, * $k$ 는 무작위 값으로 선택**한다.
서명 생성 절차는 아래와 같다.
- 서명해시 $z$ 가 주어지고 비밀키 $e$ 는 이미 알고있다.
- 임의로 $k$ 값을 선택한다.
- $R=kG$ 로부터 $R$ 의 $x$ 좌표값인 $r$ 을 계산한다.
  - 이 때, $r=0$ 이면 다시 $k$ 를 선정한다.
- $s=(z+re)/k$ 를 계산한다.
  - 이 때도 동일하게 $s=0$ 이면 다시 $k$ 를 선정하는 과정으로 돌아간다.
- 서명값은 $(r,s)$ 이다.
공개키인 $P$ 는 검증자에게 보내야하고, $z$ 또한 검증자가 알고있어야한다.
뒤에서 $z$ 는 계산으로 얻고 $P$ 는 서명과 함께 전송됨을 볼 수 있을 것이다.

3.15 파이썬을 통한 서명 생성 구현

해시함수를 사용해서 아래와 같이 서명을 생성할 수 있다.

>>> from ecc import S256Point, G, N
>>> from helper import hash256
>>> e = int.from_bytes(hash256(b'my secret'), 'big') 
>>> z = int.from_bytes(hash256(b'my message'), 'big')  
>>> k = 1234567890  
>>> r = (k*G).x.num 
>>> k_inv = pow(k, N-2, N)
>>> s = (z+r*e) * k_inv % N 
>>> point = e*G 
>>> print(point)
S256Point(028d003eab2e428d11983f3e97c3fa0addf3b42740df0d211795ffb3be2f6c52, \
0ae987b9ec6ea159c78cb2a937ed89096fb218d9e7594f02b547526d8cd309e2)
>>> print(hex(z))
0x231c6f3d980a6b0fb7152f85cee7eb52bf92433d9919b9c5218cb08e79cce78
>>> print(hex(r))
0x2b698a0f0a4041b77e63488ad48c23e8e8838dd1fb7520408b121697b782ef22
>>> print(hex(s))
0xbb14e602ef9e3f872e25fad328466b34e6734b7a0fcd58b1eb635447ffae8cb9

이어서 메시지에 대한 서명을 생성하기 위하여 비밀키를 보관할 클래스를 작성해보자.

class PrivateKey:

		def __init__(self, secret):
				self.secret = secret
				self.point = secret * G #1

		def hex(self):
				return '{:x}'.format(self.secret).zfill(64)

		def sign(self, z):
				k = randint(0,N) #2
				r = (k*G).x.num
				k_niv = pow(k,N-2,N) #3
				s = (z + r*self.secret) * k_inv % N
				if s > N/2: #4
					s = N-s
				return Signature(r,s)

주석처리된 부분을 단계적으로 살펴보자.
1. self.point 에 공개키에 해당하는 값을 계산하고 저장하는 과정을 거친다.
2. 그 후 randint 함수를 통해 [0,N] 범위에서 무작위 정수값을 정한다.
3. 이후 페르마의 소정리를 사용해 k_niv 값을 구하고 그 뒤 연산을 진행한다.
4. 또한 비트코인 트랜잭션을 전파하는 노드는 가변성 문제로 $N/2$ 보다 작은 $s$ 값만을 전파한다.