230926 Parameteric Curve (2)

• Bezier Curves
  Hermite curve의 근사 버전. 기존 Hermite curve는 $P'(0), P'(1)$이 주어질 것을 요구했지만, 일반적으로 사용자에 의해 탄젠트값이 주어지지는 않기 때문에 근사하는 방법이 선호된다.

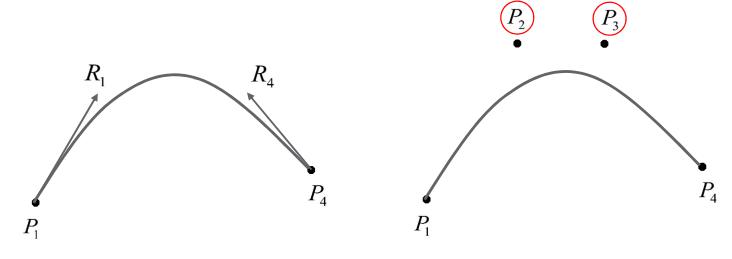
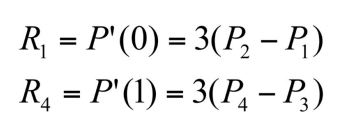
그리 어렵지 않게, Bezier curves의 basis matrix($M$)은 쉽게 얻어질 수 있다.

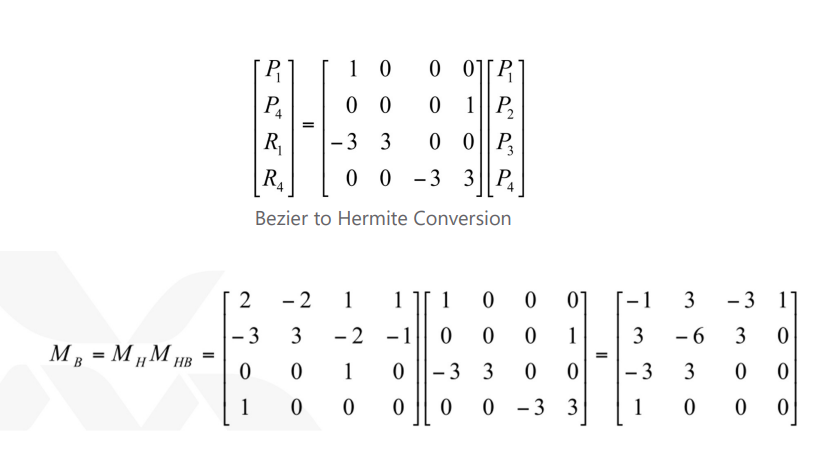
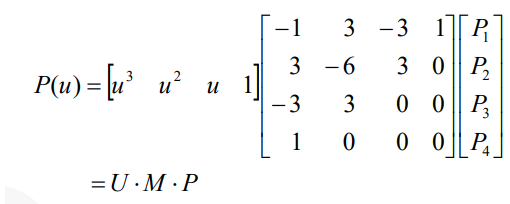
• 여기서 blending function이라는 새로운 개념이 등장한다. $U^TM$ 을 미리 계산해서 하나의 벡터로 만들면 다음과 같이 나타낼 수 있는데, 이를 blending function 이라고 한다.
  

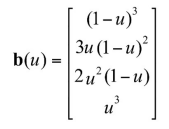
  이 개념이 갑자기 등장하는 이유는, 사실 Bezier curve의 이 blending function은 Bernstein polynomials를 사용해서 쉽게 나타낼 수 있기 때문이다. $d$는 최대 degree를 나타내고, $k$는 $k$번째 column을 나타낸다고 생각하면 된다. (0-indexed)
  
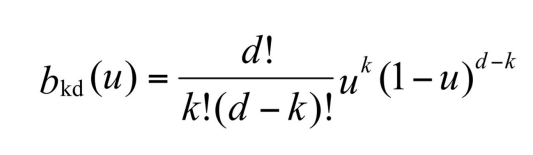
  수식이 정의 되었으니, 확장도 간편하게 된다. 따라서 점을 더 정의하거나, $u$의 degree를 늘리는 과정이 쉽게 정의될 수 있다.

• Bezier curve는 항상 Convex hull 내부에 머무르는 특성을 가져, Catmull-Rom spline이 과장된 곡선을 보이는 것이 싫다면 좋은 대안이 될 수 있다.
  
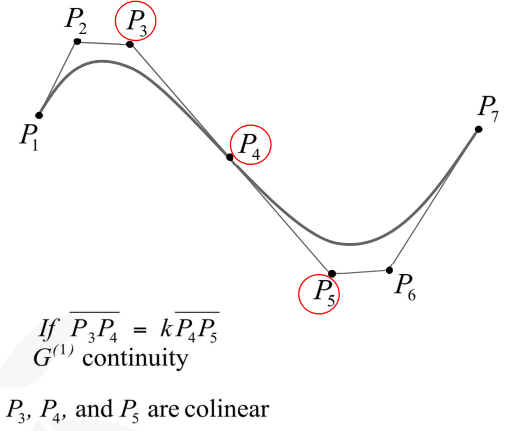
  이 곡선은 $G^{(1)}$ continuity가 보장되면 서로 다른 두 개의 Bezier curve도 쉽게 이어질 수 있다.
  
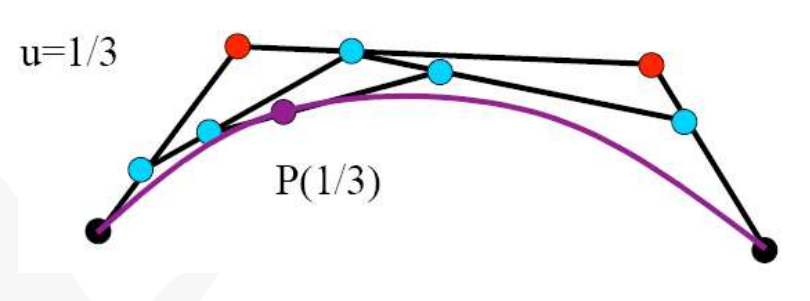
  De Castelijau algorithm이라는 방법론이 알려져 있다. 네 점을 연결했을 때 '사각형' 을 이루는 Bezier curve를 Cubic Bezier curve라 하자. 각 모서리에 $u:(1-u)$로 나눈 점들을 찍고 다시 이들을 연결하면 삼각형이 되는데, 이를 Quadratic Bezier curve라 한다. 다시 같은 방식으로 만든 선분을 다시 같은 비율로 나누면 하나의 점이 되는데, $u$의 크기에 따라 이동하는 이 점의 궤적을 그리면 그대로 Bezier curve가 완성된다.
  

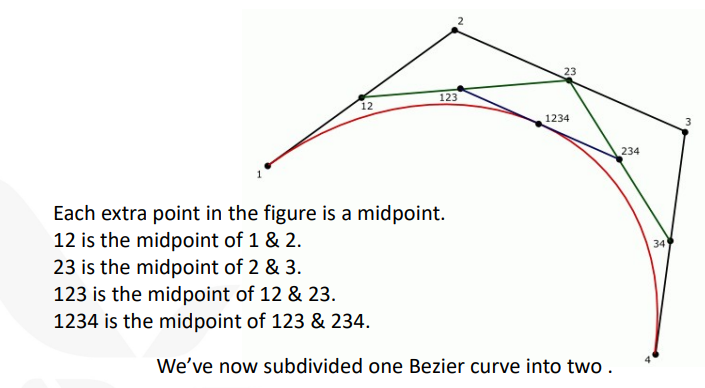
  다만 이 알고리즘은 Bezier curve를 그리기 위해서라기 보다는, Bezier curve의 분할을 할 때 더 유용하게 쓰인다. 위 그림은 $u=1/2$로 설정함으로써 Bezier curve를 반으로 나눈 결과이다.
  

• B-Splines
  Basis splines의 약자. 다른 커브들이 Interpolating을 기조로 삼았다면 B-Splines는 approximation을 기조로 삼는다. $C^2$ continuity를 가져 매우 부드럽지만 구현에는 사실상 3배의 비용이 더 들어가며, 곡면의 경우는 9배의 비용이 더 들어간다.
  
  
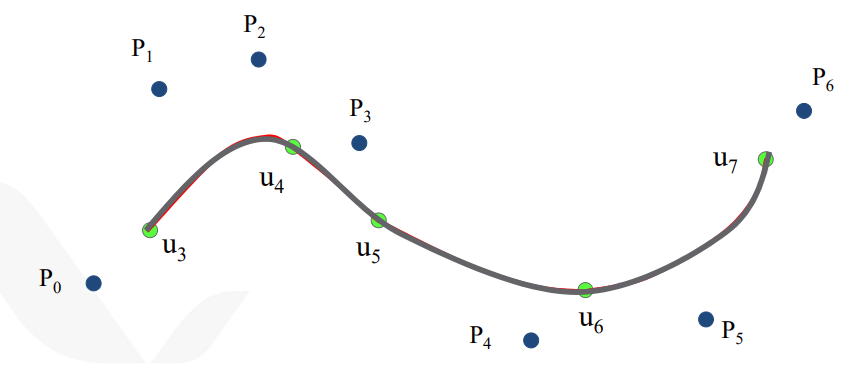
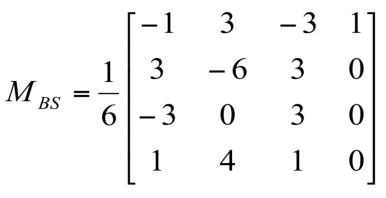
  각 정점을 4개씩 잡고, $u$를 증가시켜 나간다. $(P_0, P_1, P_2, P_3)$에 대해서는 $u\in[0,1]$, $(P_1, P_2, P_3, P_4)$에 대해서는 $u\in[1,2]$, ... 이런 식으로 위에 정의된 $M_{BS}$를 연산해 나가면 된다.
  

• B-Splines는 비싸고 요구하는 정보도 많지만, Bezier curve의 상위 버전이기도 하다. Bezier curve에서 요구되는 모든 속성들을 만족하고, 각 정점들을 로컬하게 조정 가능한 점 때문에 더 나은 컨트롤 가능성을 주기 때문이다.
  

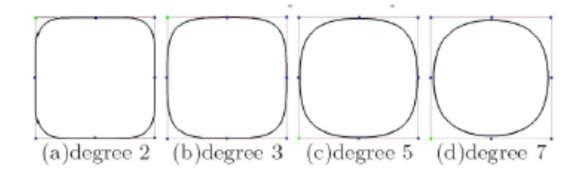
  그렇다고 B-Splines가 만능이라는 것은 아니다. 여전히 B-splines는 polynomial curve이기 때문에, 원이나 타원 같은 간단하지만 자주 쓰이는 모양은 표현하지 못한다. 더 구체적으로 표현하면, 'Conic sections를 나타내지 못한다' 고 한다.
  

• NURBS (Non-uniform rational B-splines)
  
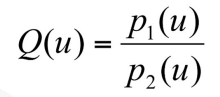
  위에서 제시된 $Q(u)$는 NURBS curve라고 부른다. $p_1(u)$와 $p_2(u)$라는 polynomial을 사용해서 사용자는 Belzier curve와 B-splines의 일반화된 버전의 커브를 마음대로 제작할 수 있다.