231017 Parametric Surfaces

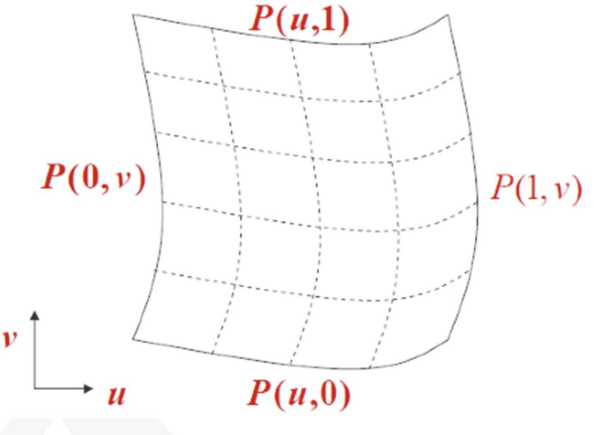
• 곡선이 $x(u), y(u), z(u)$로 정의됐던 것처럼, 곡면은 $x(u,v), y(u,v), z(u,v)$ 형태로 정의될 수 있다.

• 또한 커브가 $UMP$로 정의되었던 것처럼, 똑같이 $VMP$로 $v$에 대한 연산이 추가로 고려된다.
  

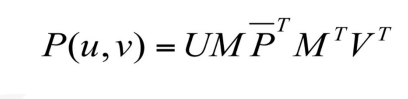
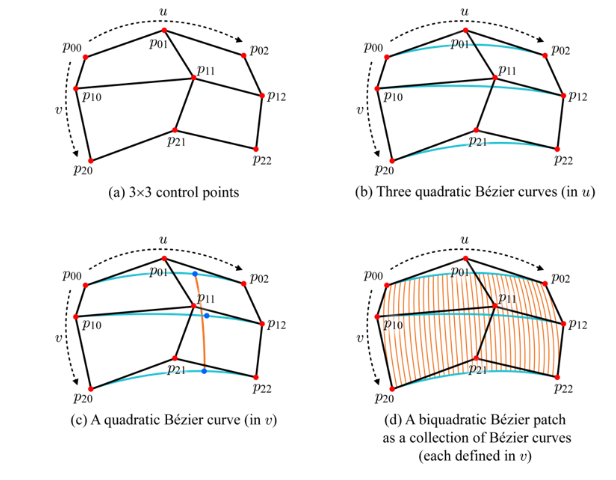
• 그런데 이렇게 쓰니 솔직히 잘 모르겠다. 아래에 더 좋은 예시가 있다. 예시는 베지어 2차 커브에 대해서 기술하고 있다.
  
  

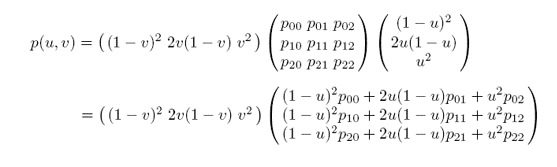
• 2차 베지어 곡선을 먼저 3개 그리고, $u,v \in [0,1]$을 조절해가며 곡면이 정의되도록 한다. 이것은 수식을 활용해 개념적인 '곡면' 을 정의하는 방법이고, 어떤 solid한 물체로써 화면에 그릴 때는 다양한 것들이 고려되어야 한다. 일단은 곡면 정의법만 머리 속에 넣으면 된다.

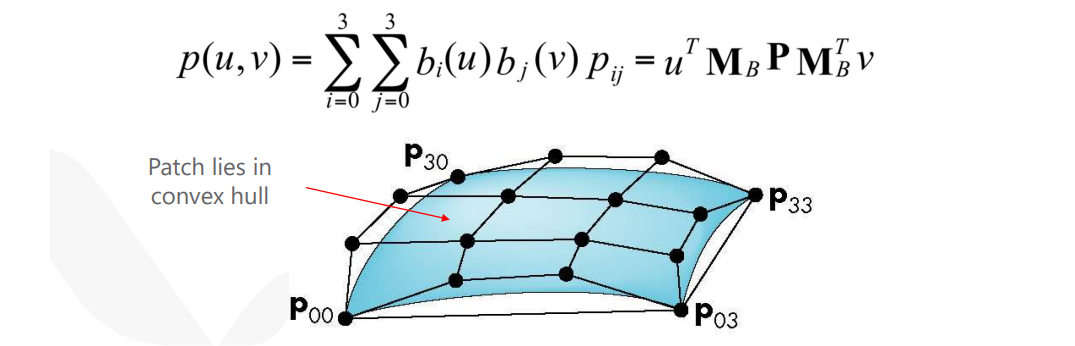
• $P$는 곡선에서는 각각 $x, y, z$ 축에 대응되는 좌표값들을 모아둔 하나의 벡터였다. 여기서도 마찬가지지만, 이제는 정사각 행렬로써 표현된다.
  

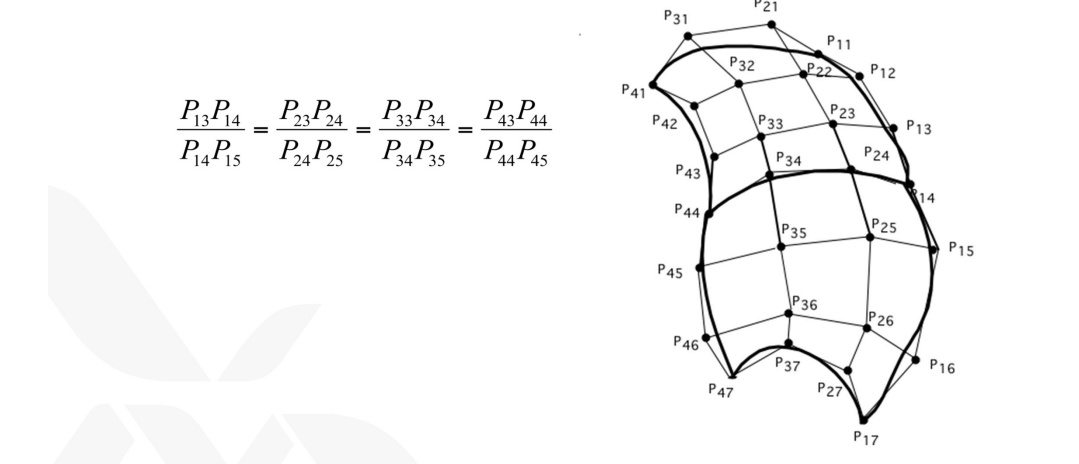
• 두 개의 베지어 곡면을 이을 때는 두 가지 방법 가능성이 있다.
  1) $C^1$ 연속성으로 잇기: 맞닿은 4개의 점을 공용으로 쓰게 만듦
  2) $G^1$ 연속성으로 잇기: 맞닿은 4개의 점만이 아니라 각 점의 양쪽 탄젠트도 서로 같아야하며, 각 점의 양쪽 점들(총 3개의 점) 간 거리는 모든 4개의 지점에서 다 비율이 같아야 한다.
  

• B-Spline 곡면
  

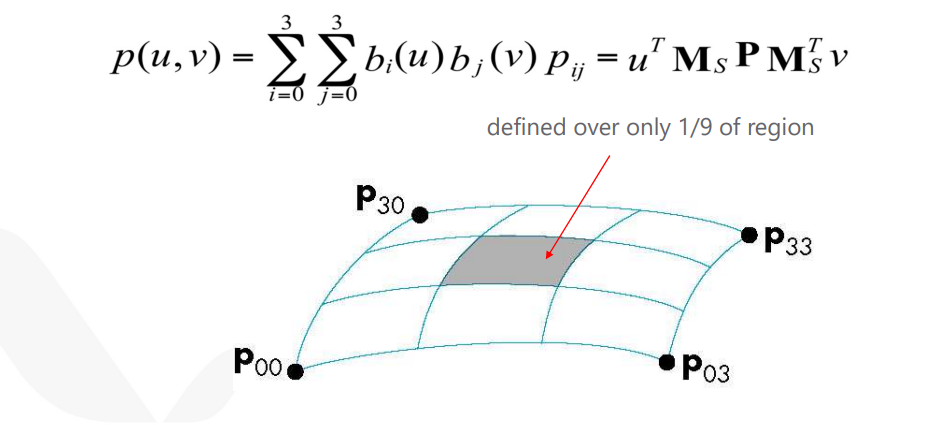
  B-Spline 곡선을 그대로 입체화 시킨다. 대신 위치는 양 끝 두점만 사용하고, 나머지는 탄젠트 표현에 사용하므로 4개의 점을 조정하며 영향을 미치는 곡면은 9개의 면밖에 되지 않는다.

• NURBS 곡면
  Non Uniform + Rational + B-Spline. 복잡하지만 플렉시블 하고 강력하다. Conic도 쉽게 나타낼 수 있으며, CAD에서 주로 사용된다.

• Subdivision Surfaces
  한번 정의된 매개변수화 곡면을 더 세부적으로 조정하고 싶은 상황이 생긴다. 하지만 이것을 하려면 매번 새롭게 매개변수화 곡면을 정의하고 '갈아 끼우는' 작업을 해야한다. 매번 번거롭게 이러지 말고, 기존에 존재하는 곡면을 나누는 방법을 개발하면 된다.
  두 가지 과정이 있는데 1) Topological division 2) New geometry computation 으로 나뉜다. 여기서 Topological division을 어떻게 하는가에 따라서 엄청 다양한 방법들이 있다.
  

• Subdivision Surfaces 방법론의 분류
  

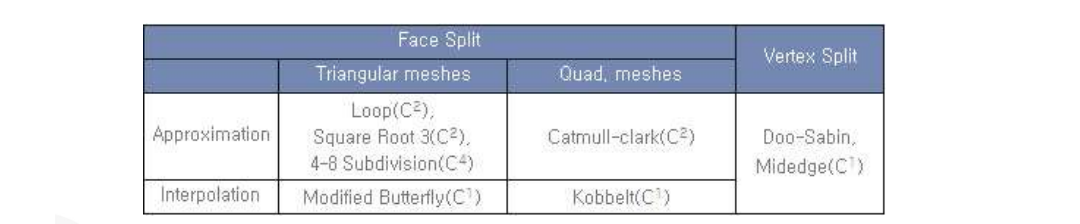
1) Face split: 기존 꼭지점은 그대로 냅둔 채 모서리들을 반반씩 쪼개서 4개로 쪼개는 방법. 사각형으로 쪼개는 방법과 삼각형으로 쪼개는 방법이 있다.
2) Vertex split: 기존 꼭지점을 4개로 쪼개서 조인트를 만드는 방법.
3) Interpolation: Bezier Spline 식. 원본 조인트들은 냅두고 그 사이에 새로운 조인트들이 생김
4) Approximation: B-spline 식. 새롭게 생긴 조인트들은 꼭 원본 곡면 위에 있지 않다. 훨씬 부드럽지만, 마찬가지로 조절되는 곡면은 적다.

• 비교
  1) Interpolation이 필요 없을 때는 Loop과 Catmull-clark가 좋다.
  2) Triangular mesh일 때는 Loop가 좋다.
  3) Quad mesh일 때는 Catmull-clark가 좋다.

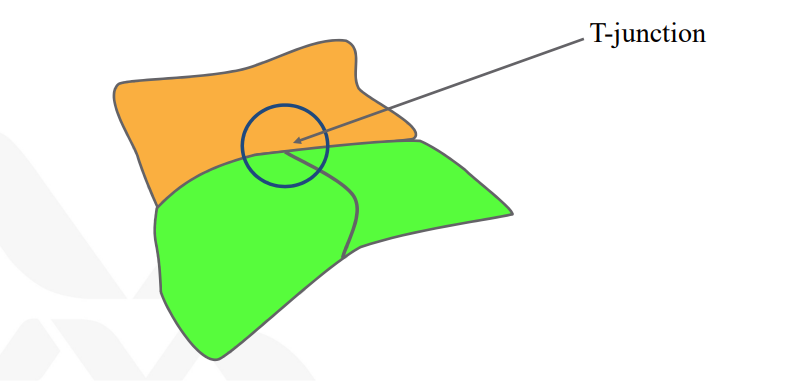
• Adaptivse subdivision - T-splines
  당연히 모든 곡면을 그냥 무작정 정직하게 4등분씩 나눌 필요는 없다. 현실적으로는 일부는 세세하게, 일부는 듬성하게 조인트가 있어도 된다. 이런 점에 있어 T-splines가 등장했다. T-junctions의 사용을 가능하게 함으로써 더 선택과 집중을 할 수 있게 된 것이다.