-
낮은 수준의 그래픽에서는 광선을 뿌리고 처음 부딪히는 물체의 색을 얻어오는 것만으로도 충분했다. 하지만 좀 더 실사같은 그래픽을 바란다면 Ray-casting algorithm으로는 부족하다.
-
Global illumination은 너무 비싸다! 대신 빛 하나가 가능한 한 많은 반사를 거친 결과를 표현하도록 하자.
-
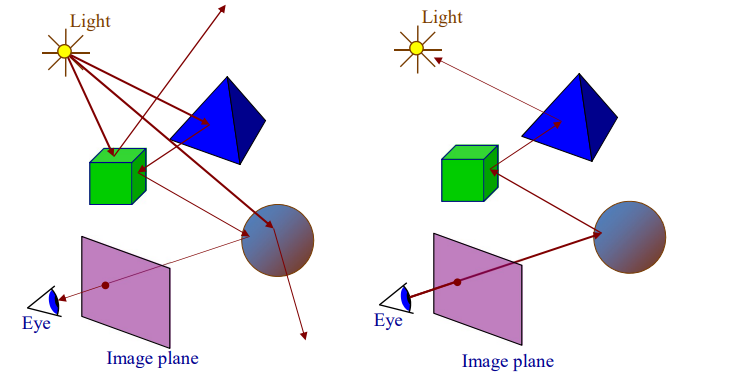
원래대로라면 광원으로부터 오는 광선을 다 반사해 계산하고, 그 광선들 중에서 image plane에 들어오는 것들을 보여주는게 진짜 레이 트레이싱(Backward ray tracing)이지만, 당연히 비현실적인 연산이다.
-
그럼 반대로 image plane에서 광선을 출발시켜서 광원의 영향력을 계산한다. 이것이 현재 쓰이는 방식의 레이 트레이싱(Forward ray tracing)이다.
-
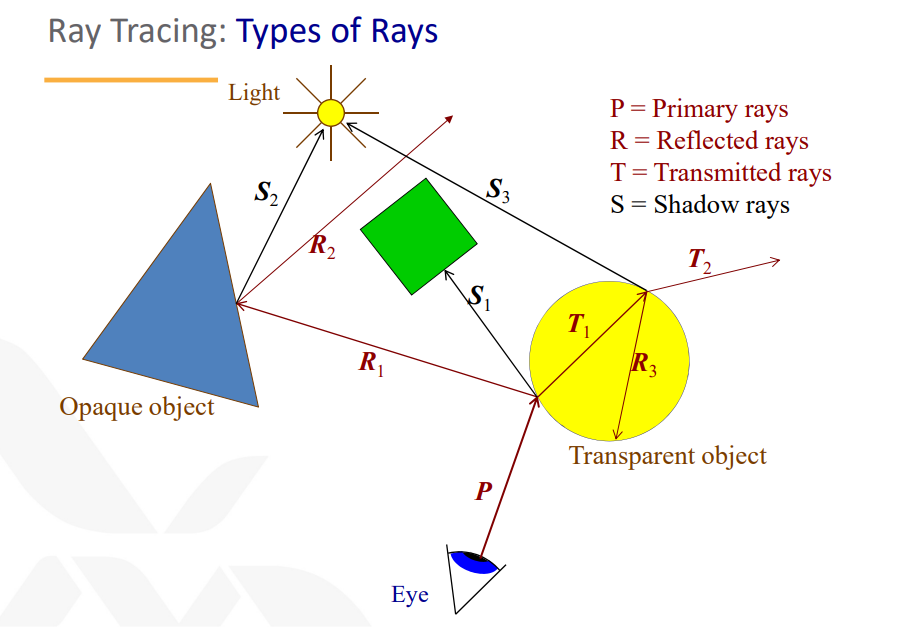
눈에서 바로 나오는 빛은 Primary rays, 반사, 투과, 그림자를 고려한 Secondary rays로 나뉜다.
-
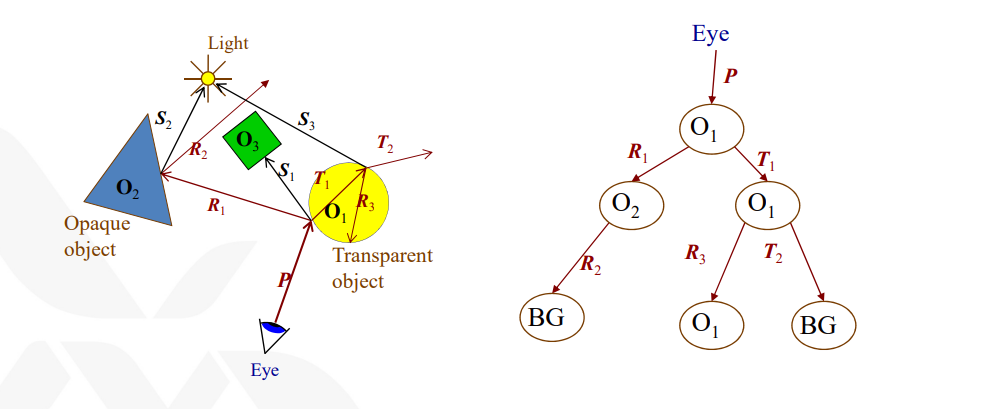
광선의 경로를 데이터로 표현하는 방법은 Ray tree를 사용하는 것이다. 노드는 부딪히는 물체, 엣지는 광선의 종류를 나타낸다. 빛을 계산할 때는 DFS를 사용하며, Trace 함수를 만드는 방법도 결국에는 재귀적으로 하게 된다.
-
헌데 문제가 있다. '물체와 부딪히는 지 여부' 를 계산하는거 생각보다 수학적으로 계산이 오래 걸린다.
-
평면과의 충돌
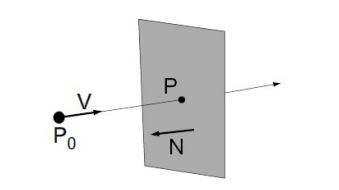
Line:
Plane: -
구와의 충돌
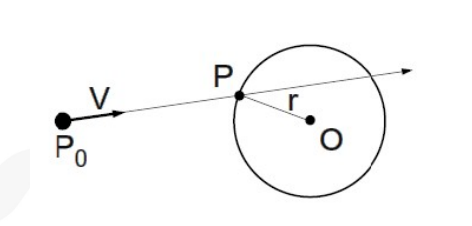
Line:
Sphere: -
다면체(polyhedra)와의 충돌
기본적으로는 평면과의 충돌과 원리가 동일하다. 대신 위 공식은 무한히 펼쳐진 평면에 대해 어느 직선이 통과하는지 여부만 검사하기 때문에, '정말 이 물체에 입구 평면과 출구 평면에 대응되는 방식으로 통과했는가?' 를 검증해야 한다.
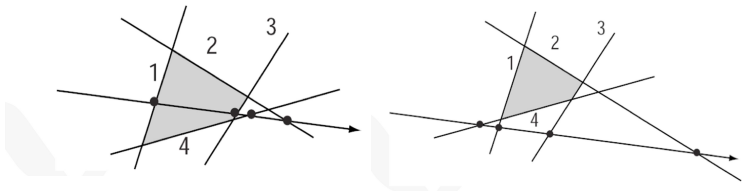
의외로 하는 방법은 간단하다. 입구 평면(1)이 가장 먼저 통과된건지 로직적으로 검증하는 것이다.
사실 다른 방법들 (Bounding box, group of bounding boxes, quad tree(octree), K-D tree) 등 다양한 방법들도 많지만 여기서는 생략한다.
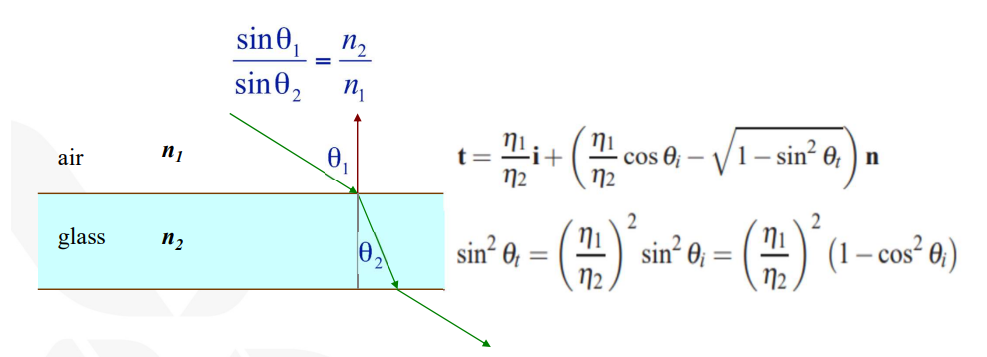
- Refraction(굴절)
스넬의 법칙을 따르며 계산된다. 한가지 고려해야 할 점은 입사각과 굴절 계수에 따라서 Critical angle이 존재하는데, 이 경우에는 빛이 투과하지 않고 반사된다. - 기본적으로 이 알고리즘은 Hidden surface removal, multiple light sources, reflections, transparent refractions, hard shadows 등을 포함한다. 하지만 더 나아가서 Soft shadows, motion blur, blurred reflections(glossiness), Depth of field (finite apertures), Translucent refractions) 등으로 더 확장될 수 있다.
