231026 Radiosity

Radiosity는 한국어로 대응되는 단어가 없다. 사전상으로는 '확산광을 계산하는 방법' 으로 정의된다.

결과적으로는 Intensity라는 (에너지/시간) 차원을 갖는 단위로 빛은 표현된다. 물리적 이론으로는 컴퓨터가 계산해내기 매우 비효율적인 적분을 포함한 식으로 표현된다.

모든 평면을 구성하는 patch가 일종의 radiosity라는 특성을 갖고 있다고 가정한다. radiosity는 flux (에너지/(단위면적*단위시간))으로 구성되는 물리 단위를 사용한다.

결국 '그 patch는 빛을 얼마나 뿜는가?' 를 고려하게 되는 것이다. 따라서 원래 그 면적에서 나오는 빛 $e$와 빛이 입사됐을 때 얼마나 빛을 뿜는가에 대한 radiosity $b$에 대해서 다음과 같이 세가지 물리량을 구할 수 있다.
1) 에너지 총량 : $b_ia_i=e_ia_i + \rho_i \sum{f_{ji} b_ja_j}$
2) Radiosity 등식 : $b_i = e_i + \rho_i \sum{f_{ij} b_j}$
3) Reciprocity 등식 : $f_{ij}a_i=f_{ji}a_j$

$b$는 radiosity, $e$는 emission, $a$는 area, $\rho$는 reflectivity, $f_{ij}$는 $j$번째 patch에 들어온 에너지에 반응해서 $i$번째 patch에서 얼마만큼 에너지가 나가는가? 에 대한 기술이다. $f$의 아랫첨자는 뒤에서 앞으로 읽어야 한국어에서는 이해가 자연스럽다.

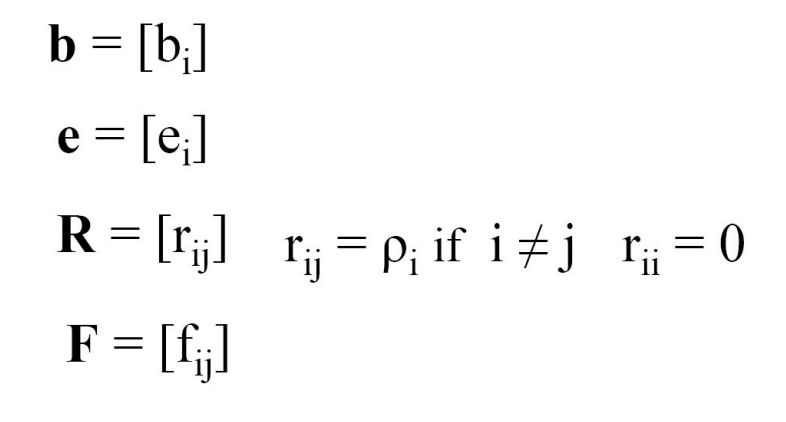
이제 여러개의 patch에 대해서 행렬로써 일반화 할 수 있다.

하지만 실시간 알고리즘에서 역행렬 계산은 금물이다. 이에 대한 근사 대책으로써, 한가지 가정을 할 것이다: $F$는 매우 sparse 한 행렬이다.

Jacobi's method

또한 역행렬은 급수로써 다음과 같이 근사될 수 있다.

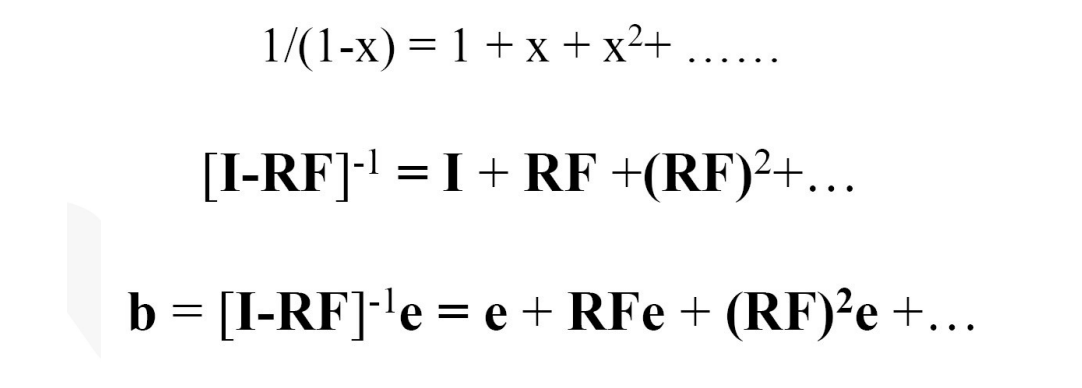
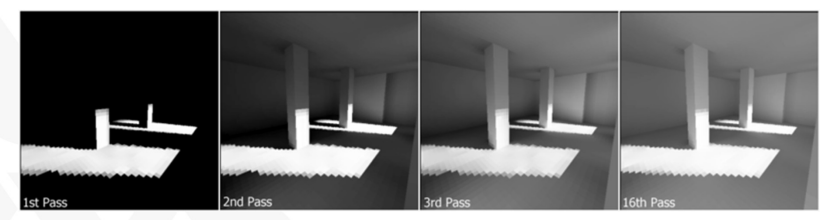
급수를 얼마나 많이 쓸 것인가에 따라서 radiosity 렌더링 퀄리티는 크게 달라진다.

Form factor의 계산

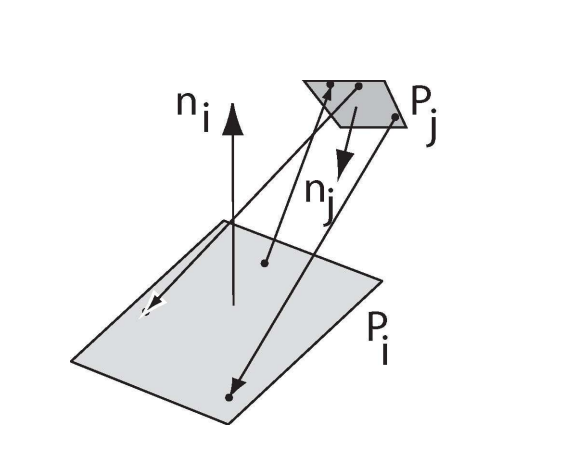
말로만 정의는 쉽게 하지만, $f_{ij}$는 다양한 요소에 영향을 받는다.
1) 각 패치 모양
2) 두 패치의 상대적 각도
3) 두 패치의 거리
4) 다른 패치에 의한 가림
의외로 빛과는 독립적이다.

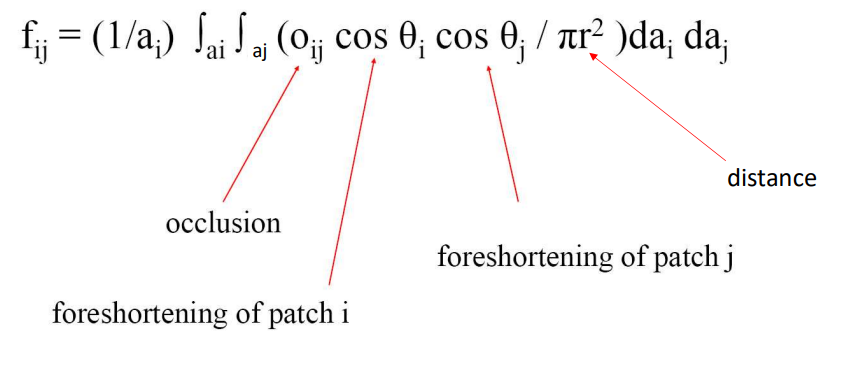
결국에는 다시 매우 비효율적인 적분을 포함한 수식이 등장하는데, 이걸 컴퓨터가 풀도록 냅두진 않을거고 두 가지 numerical한 근사를 사용할 것이다.

Hemisphere
$dA_i$를 기준으로 반지름 1인 반구를 그린다. 거기서 시작점 patch인 $A_j$를 이 반구에 사영 시키고, 이 사영된 patch를 다시 반구의 밑면으로 사영 시킨다. Form factor $f_{ij}$는 밑면에 사영된 넓이 / 전체 원의 넓이로 표현된다.

Hemicube
목표 patch인 $P_i$에 대해서 각 픽셀에 대해 $\Delta f_{ij}$ 혹은 가중치를 미리 설정해놓고 시작 patch인 $P_j$를 사영시킨 다음, 사영된 넓이에 대응되는 픽셀의 가중치와 총합해 $f_{ij}$를 구한다.
일반적으로 Hemisphere보다는 더 사용하기 쉬운 방법으로 여겨진다.