Convex Optimization 노트1

커버 범위: 1장~2-3장

Convexity

• Convex set : 주어진 기하적인 집합에서 두 점을 이었을 때 그 이어진 '올곧은 선분' 을 이루는 모든 점이 다 집합에 속할 때
• Convex function : 수학적으로 다음의 관계를 만족할 때.
  $f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta) f(y)$
  $for\;all\; x,y \in dom(f), 0\leq \theta \leq 1$

  함수 $f$의 epigraph가 convex set일 때, 함수 $f$는 convex function이다. 또한 $f$가 convex function이며, 어느 한 점 $x$에 대해서 $f(x)$가 locally optimal point일 때, 사실 $x$는 globally optimal point 이다.

Affine

• Affine set : 일반적으로 정의되는 직선이 있다고 하자. 이때 어떤 집합 $C$가 존재하며, 이 직선이 $C$에 포함된다면 이는 affine set이라고 한다.

  set C에 속한 두 점을 선형 결합 하되, 계수의 합을 1로 제한한 것이 line의 정의라 봐도 무방하며, 그렇게 정의된 C가 다시 set C에 포함된다면, 이 집합 C는 Affine set이 된다.

  • 계수의 합을 1로 제한한 것은 직선을 선분으로 만든다는 뜻이 아니다. 선분이 만들어지려면 계수의 합이 1인 동시에 $0\leq\theta\leq1$ 을 만족해야 한다.

• Affine combination : 위에서 언급한 대로 선형결합을 할 때 계수의 합을 1로 제한한다면, 이를 affine combination이 된다.

  어떤 집합에 속하는 점들을 affine combination 했을 때 그 결과가 다시 집합에 속하면 그 집합은 affine set이라고 말할 수 있다.

• Affine hull : 집합 C에 포함되는 점들의 모든 affine combination 집합을 affine hull이라고 한다. 보통 aff $C$ 라고 표현한다.

  Affine hull은 집합 C를 포함하는 가장 작은 affine set이다.

  • Affine set은 두 점을 잇는 직선이 정의되는 '집합' 을 말한다. 정 헷갈리면 머리속에서 점들을 포함시키는 무한히 확장되는 2차원 평면을 그려도 무방하다.
  • Affine hull은 affine set 속에서 정의되는 affine combination을 원소로 갖는 집합이다.
  • 따라서 affine hull은 affine set을 이루는 아주 기초적인 뼈대라고 머리속에서 이해해도 된다.

• Affine set $C$가 있을 때, 만약 $x_0\in C$라면, set $V = C-x_0$는 subspace이다.

  Affine set $C$는 linear subspace $V$를 $x_0$만큼 translation 한 것이다.

Convex

• Convex set : Affine과 비슷한 대신, 이번엔 직선 대신 선분(line segment)이다.
• Convex hull : Affine과 비슷하다. 모든 Convex combination을 포함하는 점들의 집합이며, 집합 $C$를 포함하는 가장 작은 집합이다.

  
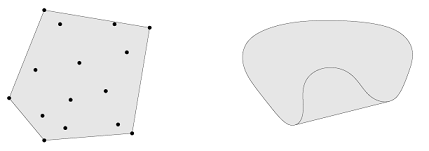
  위 그림에서는 둘 다 색칠된 영역 둘 다 convex hull을 만족한다. 오른쪽 그림과 같이 콩팥 모양의 원본 집합이 있어도, convex hull을 따지기 시작하면 오히려 더 영역이 넓어지기도 함을 주목하자.

Cone

• Cone : 앞서 정의한 Affine과 Convex와는 달리, 이번에는 반직선(ray)으로 집합을 정의하게 된다. 모든 출발점은 원점에서 한다고 가정하기에, 수식적으로도 하나의 점 $x$만 사용해서 정의된다.

  $\theta x \in C \;with\;x \in C,\;\theta \geq 0$

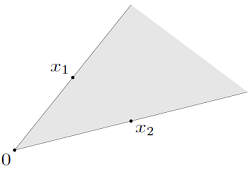
• Convex cone : 집합 $C$가 cone이면서 동시에 convex이면 이를 convex cone이라고 하며 다음과 같이 정의된다.

  $\theta_1 x_1 + \theta_2 x_2 \in C \;with\; x_1, x_2 \in C, \theta_1, \theta_2 \geq 0$

  

• Conic Combination: 이번에는 $\theta$의 범위를 $\theta_i \geq 0$ 으로만 제한해서 정의된다.

• Conic hull : 모든 Conic combination을 포함하는 집합을 일컫으며, 앞서 정의된 것과 마찬가지로 집합 $C$를 포함하는 가장 작은 convex cone이 된다.
  

Convex set examples

• Hyperplane: $n$ 차원의 공간을 반으로 가르는 $n-1$ 차원의 공간.

  $\{ x: a^{T}x=b\} \;with\; a\in R^n, a\neq 0, b\in R$

  hyperplane에 속하는 임의의 점 $x$에 대해서 $(x-x_0)$와 $a$는 직교한다. 따라서 $b=a^T x_o$ 임을 쉽게 알 수 있다.

  • Hyperplane은 affine set인 동시에 convex set이다.

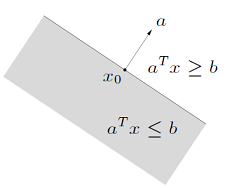
• Halfspaces: Hyperplane의 반쪽이다. 부등호 방향은 언제든 바꿔도 된다.

  $\{ x: a^{T}x\geq b\} \;with\; a\in R^n, a\neq 0, b\in R$

  • Halfspaces는 Convex set이지만 Affine set은 아니다. 무한하게 뻗어나가지 않기 때문.
  • $a^T x \geq b$ 는 normal vector 방향이 되며, $a^T x\leq b$ 는 그 반대 방향이 된다.
    

• Euclidian ball : $x_c$를 중심으로 반지름 $r$만큼의 반경 내부에 포함되는 모든 점들의 집합이며, Convex set이다.

  $B(x_c, r) = \{x | \|x-x_c\|_2 \leq r\} \; with \; r\geq 0$

  정의에 Euclidian norm이 사용되어서 이름이 유클리디언 볼이다.

• Ellipsoids : Euclidean ball과 관련된 convex set으로, 다음과 같이 symmetric-positive definite한 행렬 $P$에 대해서 다음과 같이 정의된다.

  $\mathcal{E} = \{x\;\|\;(x-x_c)^TP^{-1}(x-x_c)\leq 1\}$

  행렬 $P$는 중심 $x_c$로부터 모든 방향으로 얼마나 멀어지는가를 나타낸다.

  • 타원의 장축과 단축은 $\sqrt{\lambda_i}$로 쓰이며, $\lambda_i$는 행렬 $P$의 eigenvalue이다.
  • 유클리디언 볼은 $P=r^{-2}I$인 ellipsoid의 특별 case라고 볼 수도 있다.

• Polyhedron : 선형 부등식과 등식의 교집합. Affine set과 Convex set을 포괄하는 가장 일반적인 집합으로, 다음과 같이 정의된다.

  $\mathcal{P}=\{x\;|\;a_i^T x \leq b_i,\; i=1,...,m,\;c_{j}^{T}x=d_j, \;j=1,...,p\}$

  • 사실 등식은 두 개의 부등식으로도 표현이 가능하다. 따라서 반드시 등식을 포함할 필요는 없으며, 편의상 같이 정의된 것으로 여겨도 무방하다.
  • Polyhedron는 항상 convex set이다.
  • Bounded polyhedron을 특별히 polytope라고 부르기도 한다.

• Simplexes: n차원 공간에서 만들 수 있는 가장 간단한 도형. n+1 개의 점으로 만들어진다.

  • 엄밀하게 정의하자면, $k+1$개의 점이 있고 이들이 서로 affinely independent 하다면, 이 점들로 이루어진 convex hull이 Simplex로 정의된다.
    $\mathbb{C} = conv\{v_0,...,v_k\}= \{\theta_0 v_0 + ... + \theta_k v_k\;|\;\theta \succeq 0,\; 1^T\theta = 1\}$

Convex cone examples

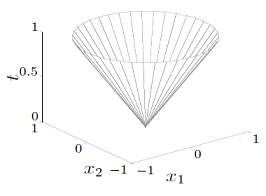
• Norm cone: 반경 $t$ 이내인 점들로 이뤄진 cone. $(x,t)$ 꼴로 $R^{n+1}$ 차원에서 정의된다.

  $C = \{(x,t):\;\|x\| \leq t\} \subseteq R^{n+1}$

  다음은 $l_2$ norm에 대한 norm cone이다.
  

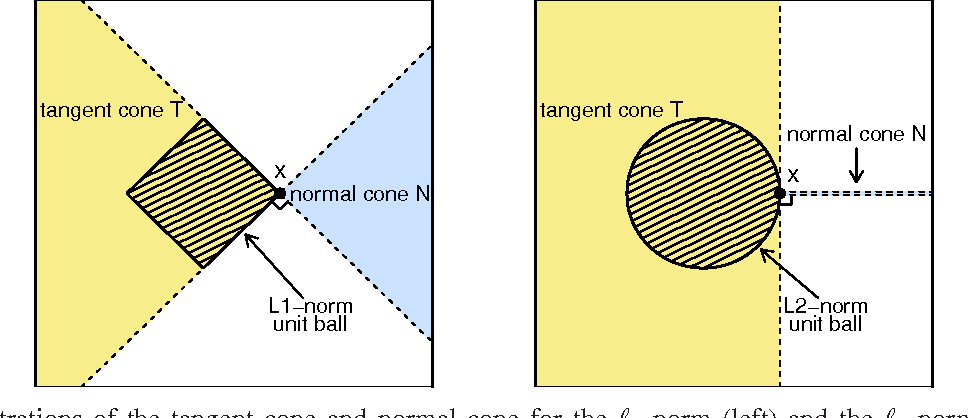
• Normal cone: 임의의 집합 $C$의 점에 대해서 한 점 $x$를 콕 찝고, 그 점과 집합 내부의 임의의 모든 점 $y$에 대해서 $x$와 연결된 벡터를 머리속에서 그리자. 이때, 이 벡터 집합들과 임의의 벡터를 내적했을 때 값이 음수가 되는 벡터들을 생각하자. 이것이 바로 Normal cone의 정의이다.

  $N_C(x) = \{g\;:\;g^T(y-x)\leq0,\;for\;all\;y\in C \}$

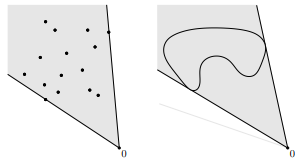
  • '모든 $y-x$에 대해서 내적값이 음수가 되는 벡터들' 이 핵심이다. 예컨대, 아래 그림에서 왼쪽 그림을 보자. 정사각형의 오른쪽 꼭지점에서 왼쪽을 가로지르는 벡터를 $(y-x)$라 한다면, 이 벡터와 $90\leq\theta\leq270$ 도를 이루는 모든 벡터들, 즉 꼭지점을 기점으로 반쪽면이 다 조건을 만족하는 것처럼 보인다.
    하지만 '모든 $y$에 대해서 고려' 해야 하므로, $(y-x)$는 정사각형을 가로지는 대각선 뿐만 아니라, 이어지는 다른 변들도 $y$와 연결된 벡터로써 고려되어야 한다. 즉, 일종의 교집합처럼 작동하는 셈이다.
    
  • $x$는 고정하고, $y$를 이동시키는 것이다.

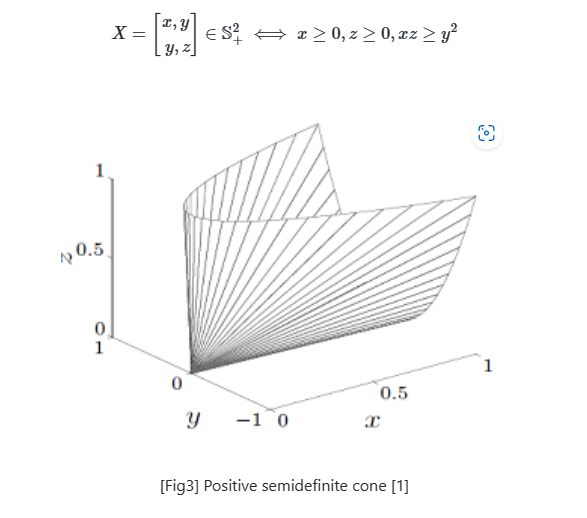
• Positive semidifinite cone: $\mathbb{S}^n$을 $n\times n$ symmetric matrix라 하자. 이 때 positive semi-definite는 다음과 같이 수식으로 정의된다.

  $\mathbb{S^n_+}=\{X\in \mathbb{S}^n\;:\; X \succeq 0 \}$

  여기서 한번 더 조건을 걸어서, $A, B \in \mathbb{S^n_+}$ 를 만족하는 행렬들과 $\theta_1, \theta_2 \geq 0$을 만족하는 변수들에 있다고 하자. 이러면 다음과 같이 일반화 시킬 수 있다.

  $\theta_1 A + \theta_2 B \in \mathbb{S^n_+}$

  convex cone의 정의와 정확히 일치한다. 따라서 positive semi-definite cone $\mathbb{S^n_+}$은 convex cone이라 봐도 무방하다.

  다음은 $\mathbb{S^2_+}$의 boundary를 3차원에서 그려낸 것이다.