Convex optimization 노트2

operations that preserve convexity

가장 기초가 되는 hyperplanes, halfspaces, norm balls와 같은 convex set을 배웠다. 이것을 원하는대로 주물러서 원하는 convex set을 만든다고 할 때, 이런 convexity를 유지하는 연산자들이 유용하게 사용된다.

• Intersection: Convex set의 교집합이다. 두개의 convex set에 대해서 교집합을 취해서 나온 집합은 항상 convex set이다.
  이런 점에서 착안해, convexity는 무한한 halfsapce의 교집합으로 다음과 같이 수학적으로 표현된다.

  $S=\bigcap \{\mathcal{H}\;|\;\mathcal{H}\;\;halfspace,\; S \subseteq \mathcal{H} \}$

  • 참고로, affine sets, convex cones도 교집합을 취하면 마찬가지로 그 성질을 유지한다. 이는 일반적으로 봤을 때 subspaces에 대해서도 적용되는 정리이다.

• Affine functions: $A\in R^{m\times n}$, $B\in R^m$ 이라고 할 때, $f(x)=Ax+b$를 affine function이라고 한다. 이제 여기다가 convex set을 넣는다고 하자. Convex set인 두개의 집합 $C\subseteq R^n$, $D\subseteq R^m$을 정의한다고 할 때, 다음이 성립하게 된다.

  • Affine image는 convex이다.
    $f(C) = \{f(x)\;|\;x\in C\}$
  • Affine preimage는 convex이다.
    $f^{-1}(D) = \{x\;|\;f(x)\in D\}$

이 정의 범주에 포함되는 affine function은 생각보다 다양한다.

• Scaling and translation: 입력 $x$를 단순히 선형적으로 이동하거나, 몇 배로 스케일링 하는 작업
• Projection: 선형대수에서 말하는 projection과 동일하다.
  $\bold{b-p}=\bold{b}-A\hat{x}=r(\tilde{x})$
• Sum of two sets: $S_1 + S_2$
• Partial sum of set

• Perspective function: 카메라가 핀홀을 거쳐서 평면에 상을 맺히도록 그림을 그린다. 이와 같은 역할을 하도록 하는 함수로, $R^{n+1}$ 차원의 공간에 있는 물체가 $R^n$ 차원의 평면에 맺히게 된다.

  $P:R^{n+1} \rightarrow R^n$
  $dom\;P=R^n \times R_+$
  $P(z,t) = z/t$

• Lienar-fractional functions: Affine function과 Persepctive function을 합친 형태이다.

  $f(x)={{Ax+b} \over {C^T x + d}}$
  $\mathcal{dom} f(x) = \{x\;|\;C^T x + d >0\}$
  $(A\in R^{m\times n}, b\in R^m, c\in R^n, d\in R)$

Generalizaed inequalities

n차원의 공간에서 두 점의 우위를 비교하기 위해서 다양한 방법이 정의되어 있다. 여기서는 generalized inequality를 살펴볼 것이다.

• Proper cone: Convex cone K, $K \subseteq R^n$이 다음의 성질을 만족하면 proper cone이라고 한다.

  • K is closed (Boundary를 포함해서 정의된다. 즉, 외곽선도 포함이다)
  • K is solid (interior가 empty가 아니다)
  • K is pointed (직선을 포함하지 않는다)

머리속에서 아이스크림 콘을 그리지 말고, 3차원 공간에서 3개의 점을 향해서 무한하게 뻗어가는 반직선으로 구성된 cone을 생각하자. 이 안에서 2차원 subspace를 정의했을 때, 이 subspace는 무조건 interior가 비게 된다.
그 이유는, n-1차원 이하의 cone은 open ball을 포함하지 못하기 때문이다.

솔직히 이것의 의미는 아직 잘 모르겠다. 나중에 다시 보면 이해가 갈까?

• Generalized inequality: Proper cone의 정의를 활용하면 $R^n$의 partial ordering인 generalized inequality를 다음과 같이 정의할 수 있다.
  $x \preceq_K y \Longleftrightarrow y-x \in K$

  다시 말해, $R^n$에서도 ordering(대소 비교)를 할 수 있는 방법을 재시하고 있는 것이다. 기존 $R$ (1차원 실수)에서는 그냥 숫자만 비교하면 됐다면, 여기서는 벡터의 연산으로써 대소가 비교되는 것이다.

마찬가지로, strict partial ordering을 다음과 같이 정의할 수 있다.

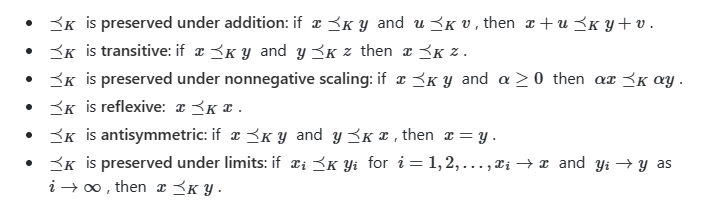
이상의 ordering 정의를 활용하여, minimum elements와 maximum elements를 계산하는 방법에 대해서 생각해볼 수 있다.

• minimum elements: $x\in S$가 모든 $y\in S$에 대해서 $x\preceq_K y$ 라면 $x$는 집합 $S$의 minimum element이다.

• minimal elements: $x\in S$가 모든 $y\in S$에 대해서 $x\preceq_K y$ 뿐이라면 $x$는 집합 $S$의 minimal element이다.

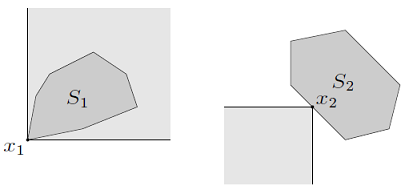
• 다음과 같이 $R^2_+$ cone 에서의 minimum과 minimal을 고려해보자.

  • $x \preceq_k y$: y가 x보다 오른쪽 위, 즉 1사분면 방향에 있다.
  • minimum $x_1$: S의 모든 점이 $x_1$의 1사분면 방향에 있다.
  • minimal $x_1$: S에는 $x_1$의 3사분면 방향에는 아무 점이 없다.
  • $x+K$: 왼쪽 그림의 옅은 회색이며, $S_1 \subseteq x+K$이므로 $x_1$은 minimum이라 할 수 있다.
  • $x-K$: 오른쪽 그림의 옅은 회색이며, $S_2 \subseteq x-K$이므로 $x_2$는 minimal이라 할 수 있다.