KCM Travel - 10217

1. 개요

원본 링크: https://www.acmicpc.net/problem/10217

2. 코드

#include <stdio.h>
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
#include <utility>
#define INF 0xFFFFFF
using namespace std;

class compare {
public:
	bool operator()(const vector<int> e1, const vector<int> e2) {
		// compare d
		return e1[2] > e2[2];
	}
};

int n, m, k, T = 0;
int memo[101][10001];
vector<vector<vector<int>>> graph;
priority_queue<vector<int>, vector<vector<int>>, compare> pq;

void dijkstra(int start) {
	vector<int> tp_start = { 1, 0, 0 };
	pq.push(tp_start);

	while (pq.size() != 0) {
		vector<int> temp = pq.top();
		pq.pop();
		int now = temp[0];
		int fee = temp[1];
		int dist = temp[2];

		// prevent loop
		if (memo[now][fee] < dist)
			continue;

		for (int i = 0; i < graph[now].size(); i++) {
			vector<int> graph_ptr = graph[now][i];
			int dest = graph_ptr[0];
			int fee_next = graph_ptr[1];
			int adj_dist = graph_ptr[2];

			int total_dist = dist + adj_dist;
			int total_fee = fee + fee_next;
			
			if (total_fee > m)
				continue;
			if (memo[dest][total_fee] <= total_dist)
				continue;
			
			for (int j = total_fee; j <= m; j++) {
				if (memo[dest][j] > total_dist)
					memo[dest][j] = total_dist;
			}
			pq.push({ dest, total_fee, total_dist });
		}
	}
}

int main(void) {
	cin >> T;
	for (int i = 0; i < T; i++) {
		int ans = INF;
		cin >> n >> m >> k;

		// init. 
		graph.clear();
		for (int j = 0; j < n + 1; j++) {
			vector<vector<int>> tp1 = {};
			graph.push_back(tp1);
		}
		for (int j = 0; j < 101; j++) 
			for (int l = 0; l < 10001; l++) 
				memo[j][l] = INF;

		// store graph inputs
		for (int j = 0; j < k; j++) {
			int u, v, c, d = 0;
			cin >> u >> v >> c >> d;
			vector<int> tp = { v, c, d };
			graph[u].push_back(tp);
		}

		dijkstra(1);

		for (int j = 0; j <= m; j++) {
			ans = min(ans, memo[n][j]);
		}

		if (ans == INF) {
			printf("Poor KCM\n");
		}
		else {
			printf("%d\n", ans);
		}
	}

	return 0;
}

3. 풀이 메모

처음에는 우선순위큐에 넣는 객체를 pair로 <비용, 거리> 꼴로 같이 넣은 뒤, 다음과 같이 pq에 삽입 조건을 설정했다.

if ((total_dist < memo[dest].second || total_fee < memo[dest].first) && total_fee <= m) 
{
				memo[dest].second = total_dist;
				memo[dest].first = total_fee;
				vector<int> tp = { dest, total_fee, total_dist };
				pq.push(tp);
}

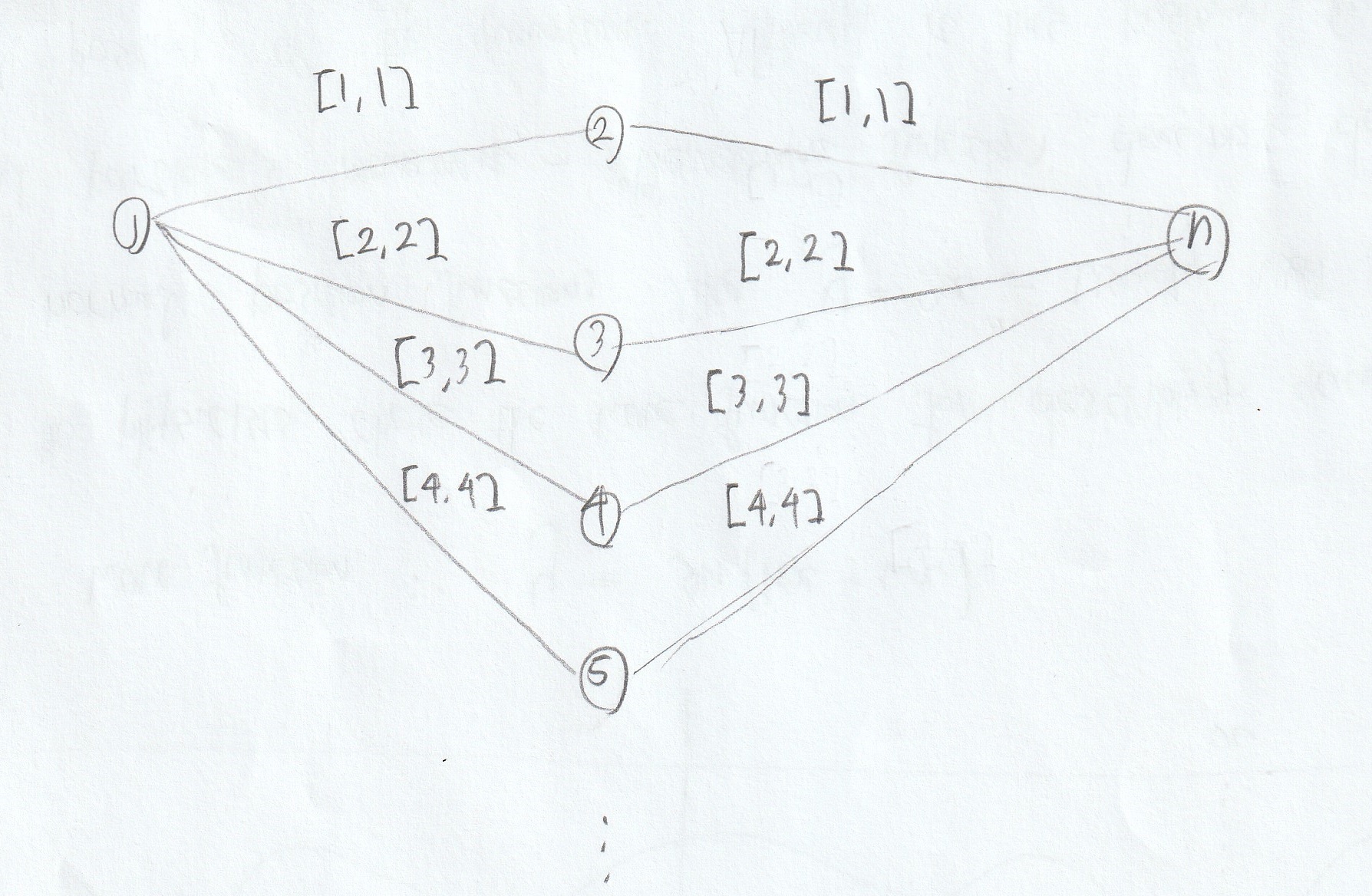
그런데 이렇게 코드를 작성하면 이미 방문한 곳도 우선순위 큐에 들어가게 되는데, 그 과정에서 비효율적으로 동작하게 된다. 특히 IF문 내부에서 dist와 fee 둘 중 하나라도 기존 DP테이블에 저장된 값보다 작을 때 삽입되도록 설계되어 있는데, 다음과 같은 양방향 그래프로 정의된 특수한 상황을 고려해보자.

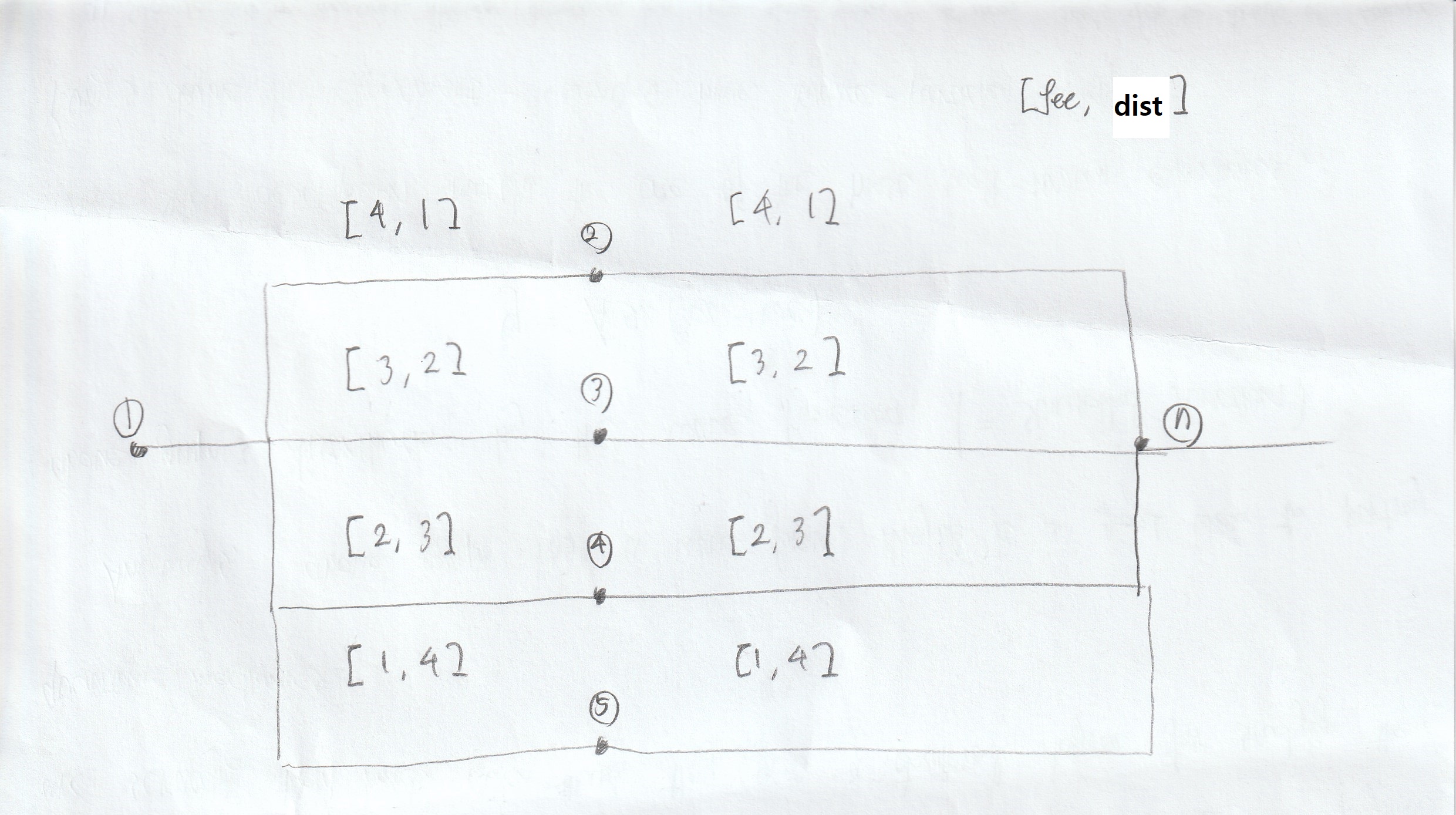
먼저, dist가 짧은 1->2가 우선적으로 고려되며, 이후 2->n이 처리되어 DP테이블에 n열에는 [8, 2]가 저장된다. 이후 1->3이 고려되며, 노드 n에 도달했을 때는 [6, 4]가 될 것이다. 이때, 노드 2에 저장된 DP 테이블 값은 [4, 1] 이기에, 우선순위 큐에는 결국 모든 n->2로 가는 간선이 또 다시 저장된다. 이는 노드3, 노드4에서도 마찬가지이며, 결국 모든 간선을 다 고려하는 것과 유사한 작동 양상이 된다.

인터넷에서 찾은 다른 방법은 2차원 배열을 기반으로 동적계획법을 사용하는 것인데, 그 방법이 (동적계획법이 늘 그렇듯이) 꽤 생소하다.

memo[목적지][비용(fee)]

다음과 같이 DP 테이블을 정의한다. 이렇게 정의된 memo[][] 내부를 이루는 원소는 거리(dist) 정보이다. 이 DP 테이블이 내포하고 있는 의미는 다음과 같다.

현재 "비용" 을 얼마나 갖고 있는가? "목적지" 까지 그 "비용" 으로는 갈 수 있는가?

예컨대 노드1에서 노드2까지 가는데는 최소 4의 비용이 필요하다. 따라서 4 이상의 예산을 갖고 있다면, 그 목적지까지는 갈 수 있다는 것이다. 여기서 다익스트라 알고리즘을 엮어서 해당 지점에 도달하는데 필요한 최소 거리(total_dist)에 대한 정보를 얻어내 memo[][] 내부에 저장하면, 결국 다음과 같은 정보를 저장하는 행렬을 얻게 된다.

그 "비용" 으로 "목적지" 까지 가는데 거치는 "최소 거리" 는 얼마인가?

이를 맞춰서 작성한 코드는 다음과 같다.

for (int j = total_fee; j <= m; j++) 
            {
				if (memo[dest][j] > total_dist)
					memo[dest][j] = total_dist;
			}

total_fee 이상의 모든 열에 대해서 최소 거리를 넣으면서 초기화 해주면, 언제 어디서나 "저 비용 m만큼 있는데, 목적지 n까지 갈 수 있나요? 최소 거리는 어떻게 되나요?" 에 대한 물음에 답할 수 있게 된다.

4. 코멘트

다익스트라 알고리즘이라고 하긴 구조가 좀 다른 것 같다. 인터넷에 보면 트리 순회 문제로 분류하는 경우도 종종 볼 수 있다.