The Laplacian Matrices of Graphs : Algorithms and Applications

강의 원본: https://www.youtube.com/watch?v=EjpMnU79neo

Interpolation of Graphs

• 최종 목표는 다음과 같다.

  $Minimize \sum_{(a,b)\in E} (x(a)-x(b))^2=x^TLx$

  여기서 $x(\cdot)$는 해당 정점에 대응되는 실수이다. 여기서 문제는 라플라스 행렬을 최소화 시키는 문제로 귀결된다.

• 즉, Graphs with positive edge weights이면 이 방법은 항상 사용될 수 있다.

Spectral Graph Theory

• n * n symmetric matrix는 n개의 eigenvalue와 eigenvector를 갖고 있다.
• 이 고유값과 고유벡터는 그래프에 대해서 많은 것을 알려준다.
• Courant-Fischer Theorem
  $\lambda_1 = min_{\| x \|=1} x^TLx$
  $v_1 = arg min_{\|x\|=1} x^TLx$
  $For \quad x^TLx=\sum_{(a,b)\in E} (x(a)-x(b))^2$
  $\lambda_1=0$ 과 $v_1$은 constant vector이다.
• 앞서 우리가 풀려고 했던 문제는 $x^TLx$ 를 최소화 하는 것임을 기억하자. 그런데 $x^TLx$는 항상 제곱의 합이고, 따라서 반드시 양수인데, 그 계산 결과가 0이 나온다는 것($\lambda_1$이 0이니까)은 그냥 trivial한 답이다. 따라서 이 답은 무시하고, 그 다음으로 큰 양수를 갖는 고유값을 찾을 것이다.

Spectral graph drawing

• 여기서 각 정점을 실수 벡터로 대응시키는 어떤 함수를 생각하자.

  $V \rightarrow \mathbb{R^n}$

• 그래프에서 각 노드에 '얼마나 연결되어 있나?' 를 갖고 정점을 정하는 것처럼, 여기서는 고유벡터를 갖고 실수값을 대응시킬 것이다.

• 영상에서는 고유벡터 $(v_2(a), v_3(a))$를 각각 $x$축, $y$축에 대응시켜서 그림을 그리고 있다. 이는 각각 2, 3번째로 작은 고유값에 대응되는 고유벡터를 활용해 정점을 벡터로 대응시킨 것이다.

• 더 자세히 말하자면, 어떤 $m \times 2$를 다음과 같이 정의하자.

  $R=[u_2, u_3]$

  각각 2, 3번째로 작은 고유값에 대응되는 고유벡터를 column으로 갖는다. 이제 이렇게 만들어진 행렬에서 새로운 $(x, y)$ 유클리디언 공간에 매핑할 것이다.

  $(R_{i1}, R_{i2})$

  다시 말해, $i$번째 정점은 $R$ 행렬의 $i$번째 열의 원소들을 갖고 매핑하게 된다.

• "멋진 그래프" 를 얻고 싶다면, 대부분의 변이 짧아야 한다. 그리고 정점들은 가급적이면 퍼져있어야 하며 서로 너무 뭉쳐서는 안된다. 이를 위해서는 다음이 만족되어야 한다.

  $\lambda_2$는 가급적 0에 가까워야 한다.

• $\lambda_2$가 너무 크다면, 예컨대 $> 10/|V|^{1/2}$라면, 좋은 그래프가 그려지지 않는다.

Measuring boundaries of sets

• '멋진 그래프' 를 얻고 싶다면, 각 노드간 정점 사이의 차이가 최소가 되도록 하되, 0으로 나와서 trivial 하지 않아야 한다.
• 이러한 생각은 어떤 그래프 내 가장 작은 정점 그룹 $S$를 찾는 것으로 생각될수도 있다. 그리고 이 문제는 정확히 $\lambda_2$를 찾는 문제와 대응된다.
  
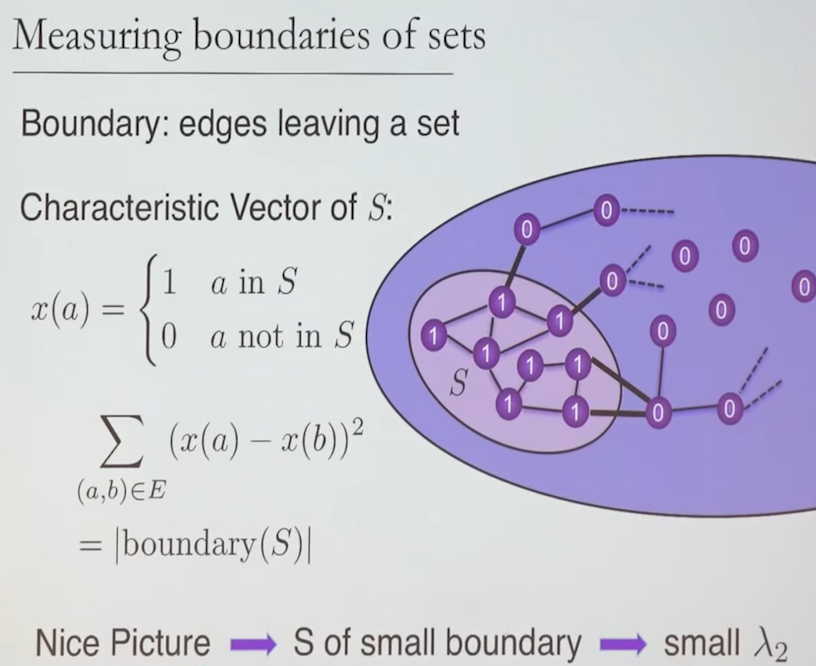
• 여기서 다시 $x^TL_Gx$ 최소화 문제로 귀결된다.

Laplacian Matrix of a Graph

• Symmetric, Non-positive off diagonals, Diagonally dominant

  각 대각행렬의 성분은 대응되는 행 혹은 열의 off-diagonal 원소들의 합의 절대값을 취한 것과 같아야 한다.

• Interior Point Methods를 사용한 Linear Programs 해결 문제에는 항상 라플라스 행렬이 수반된다.

  Maximum and min-cost flow, shortest paths, Isotonic Regression, Lipschitz Learning

Spectral Sparcification

• 모든 그래프는 비슷한 라플라스 행렬을 갖는 더 희소한 행렬로 근사될 수 있다.
• 다음을 만족하는 그래프 $H$는 원본 그래프 $G$의 $\epsilon$-근사이다.
  $\frac{1}{1+\epsilon} \leq \frac{x^TL_Hx}{x^TL_Gx} \leq 1+\epsilon$
• 이것이 의미는 원본 행렬의 boundary 정보를 그대로 갖는 희소 행렬을 찾게 되는 것이다.
• 심지어 이 Linear equation은 근사가 되어도 서로 비슷한다!
  $L_H \approx_\epsilon L_G$
  $L_H^{-1} \approx_\epsilon L_G^{-1}$

Sparcification by Random Sampling

• 어떤 그래프의 엣지 $(a,b)$를 샘플링 할 확률을 $p_{a,b}$라 하자.
• 만약 근사 그래프 $H$에 엣지 $(a,b)$가 포함되었다면, 그만큼 weight를 $w_{a,b}/p_{a,b}$ 만큼 부여할 것이다.
• 그렇다면 근사 라플라스 $L_H$의 평균은 다음과 같이 쓸 수 있다.
  $\mathbb{E} [ L_H ] = \sum_{(a,b) \in E} p_{a,b} (w_{a,b} / p_{a,b}) L_{a,b} = L_G$
• 어라, 근사 라플라스의 평균값이 오리지널 라플라스와 같네?
• 그럼 $p_{a,b}$는 어떻게 골라야 할까?
  $p_{a,b} = w_{a,b} \times effective \ resistance$
• $a$와 $b$사이의 어떤 루트가 낮은 effective resistance를 갖고 있다는 뜻은 그 루트는 그렇게 중요하지 많으며, 그 루트를 대신할 수 있는 다양한 루트가 있다는 뜻이다.
• 알려진 바에 의하면 실제 $n$개의 노드를 가진 그래프는 $O(nlogn/ \epsilon^2)$ 개의 엣지로 근사가 가능하다.

Optimal Graph Sparsification

• 모든 그래프 $G=(V,E,w)$는 다음을 만족하는 근사 그래프 $H=(V,F,z)$가 존재함이 알려져있다.
  $|F| \leq (2+\epsilon)^2 n/\epsilon^2$

Approximate Gaussian Elimination

• 어떤 라플라스 $L_G$는 다음과 같이 희소한 upper triangular matrix $U$로 근사가 가능하다.
  $L_G \approx U^TU$
  
• 위 식에서 나온 항들도 모두 라플라시안 행렬이라는 사실에 주목하라. 이 '베이비 라플라시안' 애들은 실제로는 원본 그래프에서 노드를 하나씩 삭제하는 것과 비슷한 행위이다.
  

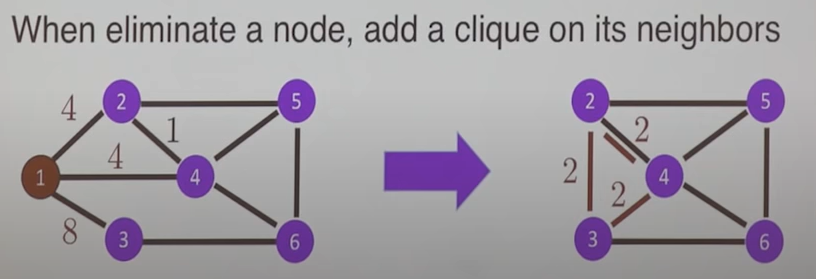
Recent Developments