[논문 리뷰] Variational quantum state diagonalization

Introduction

• 주어진 Density matrix $\rho$를 대각화 한다.
• 여기서는 행렬 대각화를 위한 Variational hybrid algorithm을 제시한다.
• 이미 qPCA와 같은 대각화 알고리즘이 있지만, 현 세대 양자 컴퓨터(NISQ)에서는 구현 불가능.
• 다음과 같은 과정을 거쳐서 알고리즘은 수행된다.
  1) $\tilde{\rho}= U_{p}(\alpha_{opt})\rho U_p(\alpha_{opt})^{\dagger}$ 를 만족하는 변수 벡터 $\alpha_{opt}$ 를 훈련한다.
  2) $\rho$를 고유 기저로 관측해서 가장 큰 고유값을 찾아낸다. 예컨대, $\tilde{\rho}$ 를 standard basis로 관측해서 얻어낸다.
  3) 이 고유값을 기반으로 상응하는 고유벡터를 얻어낸다.

Results

• 전체 구조는 다음 그림과 같다.
  
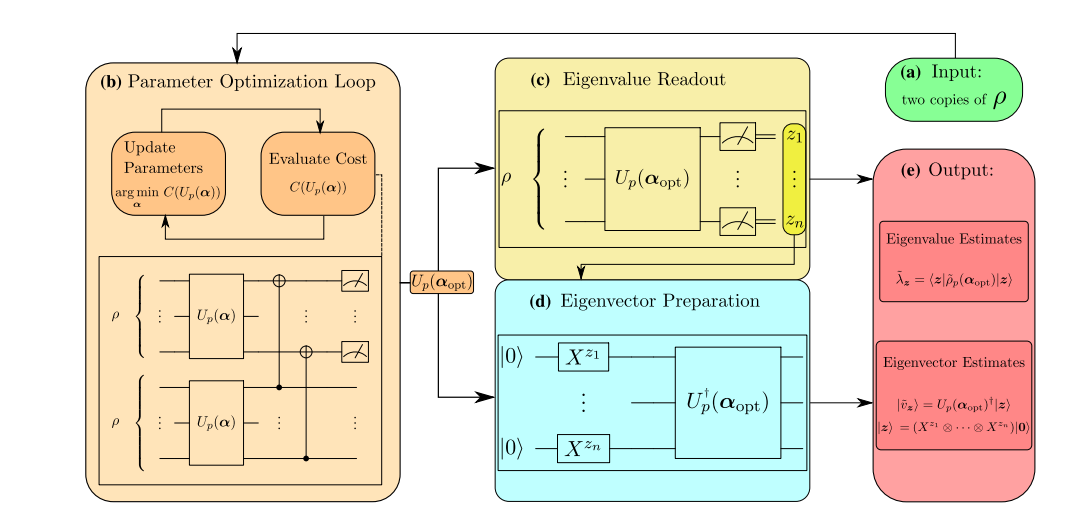
• 사용자는 몇 개의 최대 고유값을 선택할 지 m으로 선택할 수 있다. m은 $2^n$보다 훨씬 작은 값이어야 한다. $2^n$은 대각화 하려는 행렬 $\rho$의 차원이다.
• 계산되어 나온 고유값은 클래식하게 저장되고, 계산되어 나온 고유벡터는 양자 상태로 저장된다.
• 이런 류의 알고리즘이 늘 그렇듯, 정확도와 실행속도는 trade-off 관계.
• 또 하나의 다른 trade-off 관계: $N_{readout}$ 과 $m$.
• Barren plateaus를 피하는 테크닉으로, 일종의 단계적인 학습을 해나갈 것이다. $p$ 레이어의 안사츠에서 학습한 내용을 그대로 유지하며 다음 학습의 시작포인트로 삼아서 $p+1$ 레이어에서의 학습을 수행하는 것이다.
• 비용 함수 $C$는 고유 시스템(eigen system)의 정확도와 긴밀하게 연관되어있다. 만약 $C$가 줄어든다면, 더 타이트한 에러의 상한(upper bound)가 결정되게 된다.
• 대각화 결과를 평가하기 위해서 다음과 같이 두 가지 양적 기준을 정의한다.
  1) Eigenvalue error
  $\Delta_{\lambda} : = \sum_{i=1}^{d}(\lambda_i - \tilde{\lambda_i})^2$
  2) Eigenvector error
  $\Delta_\nu :=\sum_{i=1}^d \langle\delta_i | \delta_i \rangle$
  $|\delta_i \rangle = \rho |\tilde{v_i} \rangle - \tilde{\lambda_i} |\tilde{v_i} \rangle = \sqcap_i^{\bot} \rho |\tilde{v_i} \rangle$
  여기서 $|\delta_i\rangle$는 $\rho |\tilde{v_i} \rangle = \tilde{\lambda_i} |\tilde{v_i} \rangle$를 $|\tilde{v_i} \rangle$와 수직인 subspace에 사영시킨 결과가 된다. 다시 말해, '얼마나 $\rho$가 대각화가 되었는가' 를 나타내는 지표가 되어준다.

  임의의 직교 벡터 $|\tilde{v_i} \rangle$에 대해서, $\sum_{i=1} \langle \tilde{v_i} | \rho^2 | \tilde{v_i} \rangle = Tr(\rho^2)$ 가 성립한다. $|\tilde{v_i} \rangle$가 고유 벡터가 아니어도 된다는 점에서 명심하고 있으면 좋은 성질이다.