플로이드 - 11404

1. 개요

문제 링크: https://www.acmicpc.net/problem/11404

2. 코드

#include <stdio.h>
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 0xFFFFFF
int n, m = 0;
std::vector<std::vector<int>> memo;

void floyd_warshall() {
	for (int i = 1; i <= n; i++) {            
		for (int j = 1; j <= n; j++) {       
			for (int k = 1; k <= n; k++) {    
				if (memo[j][i] != INF && memo[i][k] != INF) {
					memo[j][k] = std::min(memo[j][k], memo[j][i] + memo[i][k]);
				}
			}
		}
	}
}

int main(void) {
	std::cin >> n;
	std::cin >> m;
	for (int i = 0; i < n + 1; i++) {
		std::vector<int> vec;
		for (int j = 0; j < n + 1; j++) {
			vec.push_back(INF);
		}
		memo.push_back(vec);
	}

	for (int i = 0; i < m; i++) {
		int a, b, c;
		std::cin >> a >> b >> c;
		if (memo[a][b] > c) {
			memo[a][b] = c;
		}
	}

	floyd_warshall();

	for (int i = 1; i < n + 1; i++) {
		for (int j = 1; j < n + 1; j++) {
			if (i == j || memo[i][j] == INF) {
				printf("0 ");
			}
			else {
				printf("%d ", memo[i][j]);
			}
		}
		printf("\n");
	}

	return 0;
}

3. 풀이 메모

플로이드-와셜 알고리즘은 모든 정점에 대해서 다익스트라 알고리즘을 적용하는 알고리즘이다. 시간 복잡도는 다익스트라가 O(E*logV) 였던 것과 대비되게 O(V^3)의 효율을 갖는다.

알고리즘 구현부가 조금 특이하다. 기본 아이디어는 포커스를 '중간에 거치는 노드' 에 맞춘다는 점에 있다.

void floyd_warshall() {
	for (int i = 1; i <= n; i++) {            
		for (int j = 1; j <= n; j++) {       
			for (int k = 1; k <= n; k++) {    
				if (memo[j][i] != INF && memo[i][k] != INF) {
					memo[j][k] = std::min(memo[j][k], memo[j][i] + memo[i][k]);
				}
			}
		}
	}
}

이 코드에서는 i번째 인덱스 노드가 '중간에 거치는 노드' 가 된다. j는 출발점, k는 도착점이다. 따라서 i를 중심으로 다음 두 가지를 비교한다.

(j -> k) 로 가는 경로
vs
(j -> i -> k) 로 가는 경로

예외 상황은 다음과 같이 대응이 된다.

1) 자기 자신에게 향하는 경우 (j=k) : 루프가 대입될 수 있다. 하지만 출력해줄 때 행과 열 인덱스가 같다면 0으로 출력하는 것으로 해결할 수 있다.
2) 출발지와 목적지가 경유점을 가리키는 경우 (j == i or k == j) : 자기 자신으로 직접 향하는 경로는 항상 INF가 되므로, min 내부에서는 항상 memo[j][i] + memo[i][k]가 memo[j][k]를 선택할 것이다.

4. 코멘트

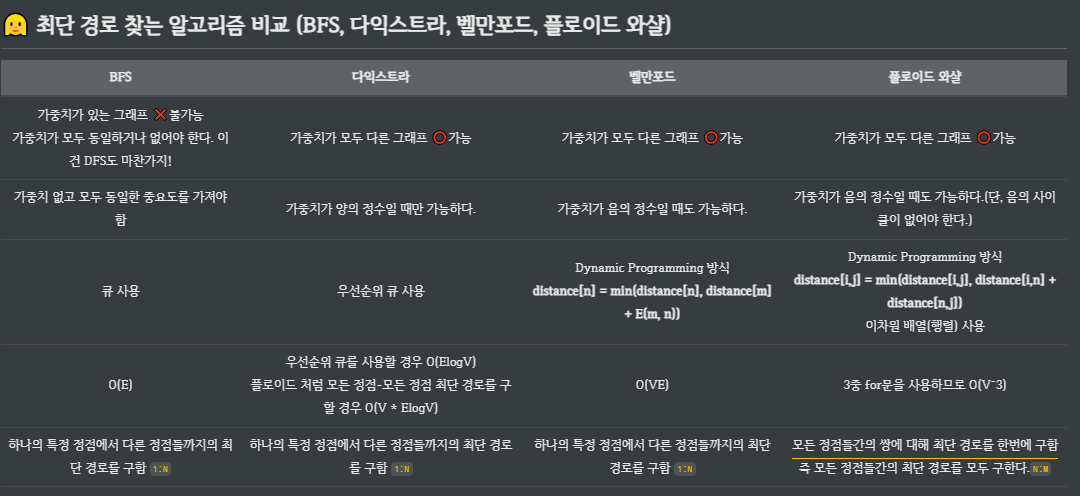
출처: https://ansohxxn.github.io/algorithm/floyd/

최단 경로 알고리즘은 여러 가지고, 각기 쓰임새가 다르다. 상황에 맞춰서 적당한 알고리즘을 선택하는 연습이 필요해보인다.