CS 실수표현 방식: 고정 소수점과 부동 소수점

코딩하는 포로리·2022년 2월 21일

CS

목록 보기

4/4

📌 1. 실수의 표현 방식

📎 실수(Real Number)란?

실수는 주로 실직선 위의 점 또는 십진법 전개로 표현되는 수 체계이다. 실수는 0보다 큰 양수, 0보다 작은 음수, 0으로 분류되며, 실직선 위의 모든 수를 표현하기 때문에 소수점 역시 포함된다.

📎 실수의 표현방식

컴퓨터에서 실수를 표현하는 방법은 정수에 비해 훨씬 복잡하다. 컴퓨터에서는 실수는 정수와 마찬가지로 0과 1 즉, 2진법으로만 표현해야 하기 때문이다. 따라서 실수를 표현하기 위한 방법으로 고정소수점과 부동 소수점을 사용하고 있다.

📌 2. 고정 소수점(Fized Point)

📎 고정 소수점이란?

실수는 보통 정수부와 소수부로 나눌 수 있다. 따라서 실수를 표현하는 가장 간단한 방식은 소수부의 자릿수를 미리 정하여, 고정된 자릿수의 소수를 표현하는 것이 고정 소수점이다.

📎 고정 소수점 구성

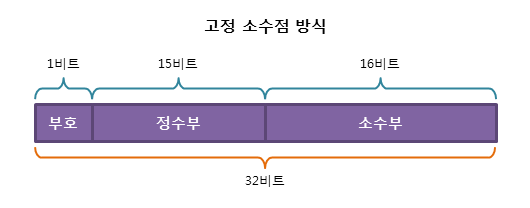
고정 소수점이 32비트일 때

👉 부호비트: 1비트

부호비트는 1비트만 가져간다. 부호비트는 실수의 부호를 나타내는 비트 자리로 실수가 음수라면 1을, 양수라면 0을 입력해준다.

👉 정수부: 15비트

정수부에서는 실수의 정수 부분을 2진법으로 표현하여 입력해준다.

👉 소수부: 16비트

마지막으로 소수부에는 동일하게 실수의 소수부분을 2진법으로 표현하여 입력해준다.

📎 고정 소수점 예시

12.125 실수를 예시로 표현하면 다음과 같다.

👉 1) 가장 먼저 12.125 실수를 부호, 정수부, 소수부로 나누어 2진법으로 구한다.

분류	이진법
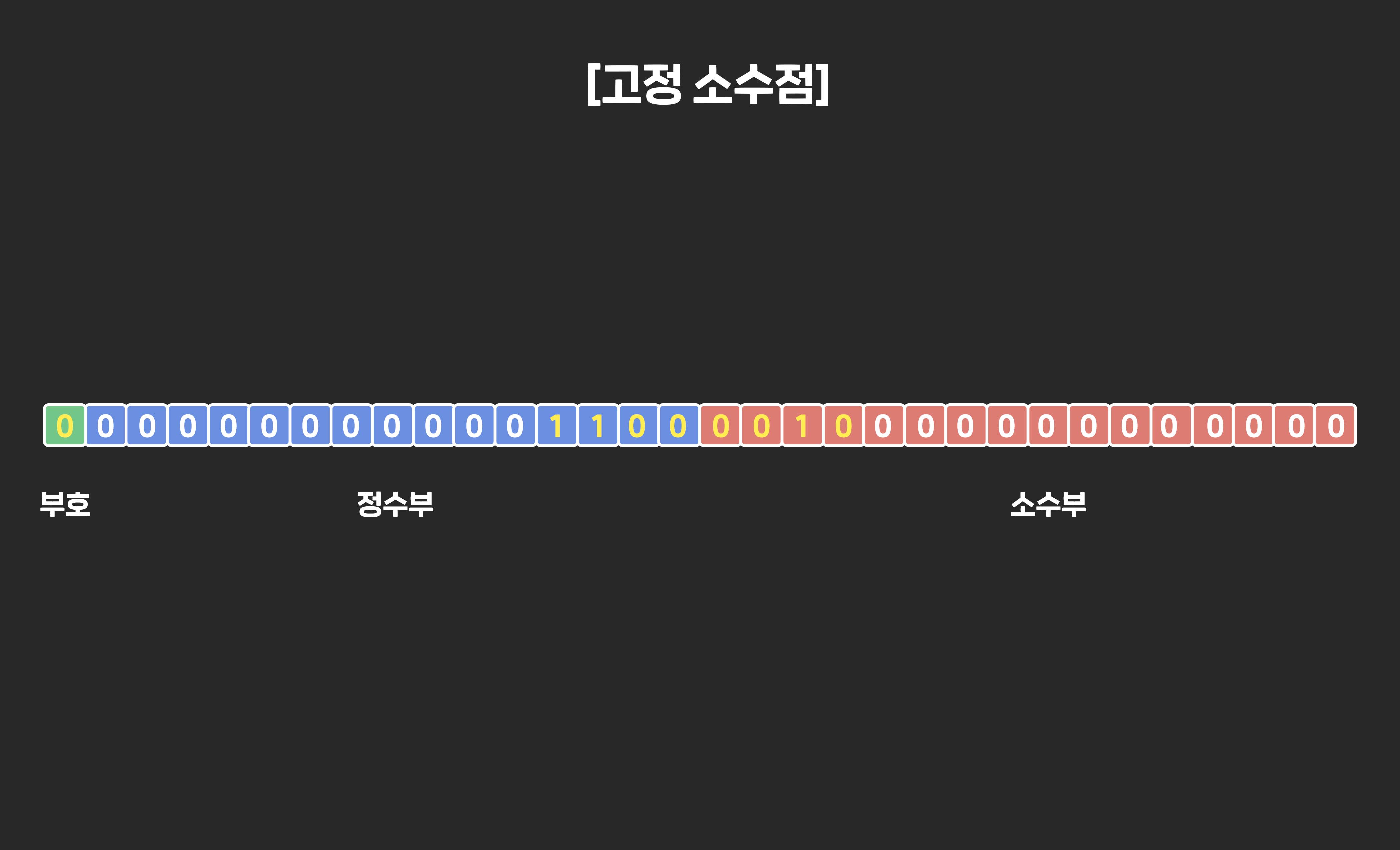
부호	0(양수이기 때문)
정수부	1100
소수부	001

👉 2) 구한 각각의 부호, 정수부, 소수부을 각 비트 파트에 입력해준다.

📌 3. 부동 소수점(Floating Point)

📎 부동 소수점이란?

고정 소수점에서 실수를 정수부와 소수부로 나눴지만, 부동 소수점에서는 가수부와 지수부로 나눈다.

📎 부동 소수점 구성

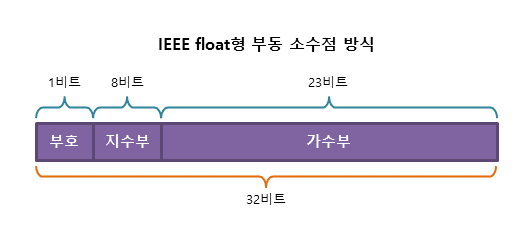
부동 소수점이 32비트일 때

👉 부호비트: 1비트

부호비트는 1비트만 가져간다. 부호비트는 실수의 부호를 나타내는 비트 자리로 실수가 음수라면 1을, 양수라면 0을 입력해준다.

👉 지수부: 8비트

👉 가수부: 23비트

📎 부동 소수점 예시

부동 소수점은 구하기 쉬운 고정 소수점과 달리 과정이 조금 복잡하다. 그래서 12.125 실수를 각각 지수부와 가수부를 구하는 상세한 과정을 설명하면 아래와 같다.

👉 1) 12.125를 이진수로 표현한다.

12.125 실수에서 .을 기준으로 12는 정수부 125는 소수부이다.
정수부에 해당하는 12를 2진법으로 바꾸면 1100 값이 나온다.
소수부에 해당하는 0.125를 1이될때까지 2를 곱해준다. 그리고 곱할때마다 나온 정수값을 차례로 나열하면 소수부인 001 값이 나온다.
최종적으로 12.125 실수를 이진법으로 바꾸면 1100.001 이라는 숫자가 나온다.

👉 2) 1100.001의 소수점을 맨 앞까지 가져간 만큼의 수를 지수로 가져온다.

1100.001의 소수점을 가장 첫번째 자리로 옮기기 위해 총 3만큼 움직이게 된다. 3을 2의 지수로 가져와 입력해준다.

👉 3) 부호 비트, 지수부, 가수를 구한다.

부호비트는 양수이기 때문에 0
지수부를 구하는 방법으로 우선 bias값인 127에 전 단계에서 구한 2의 지수 3을 더하여 130을 구한다. 그 다음 130을 이진법으로 바꾸어 10000010을 구하면 해당 값이 지수부가 된다.
가수부는 전 단계에서 소수점을 맨 앞으로 가져간 1.100001의 소수부분인 100001이 된다.

👉 4) 구한 부호, 지수부, 가수부를 각 비트 파트에 입력해준다.

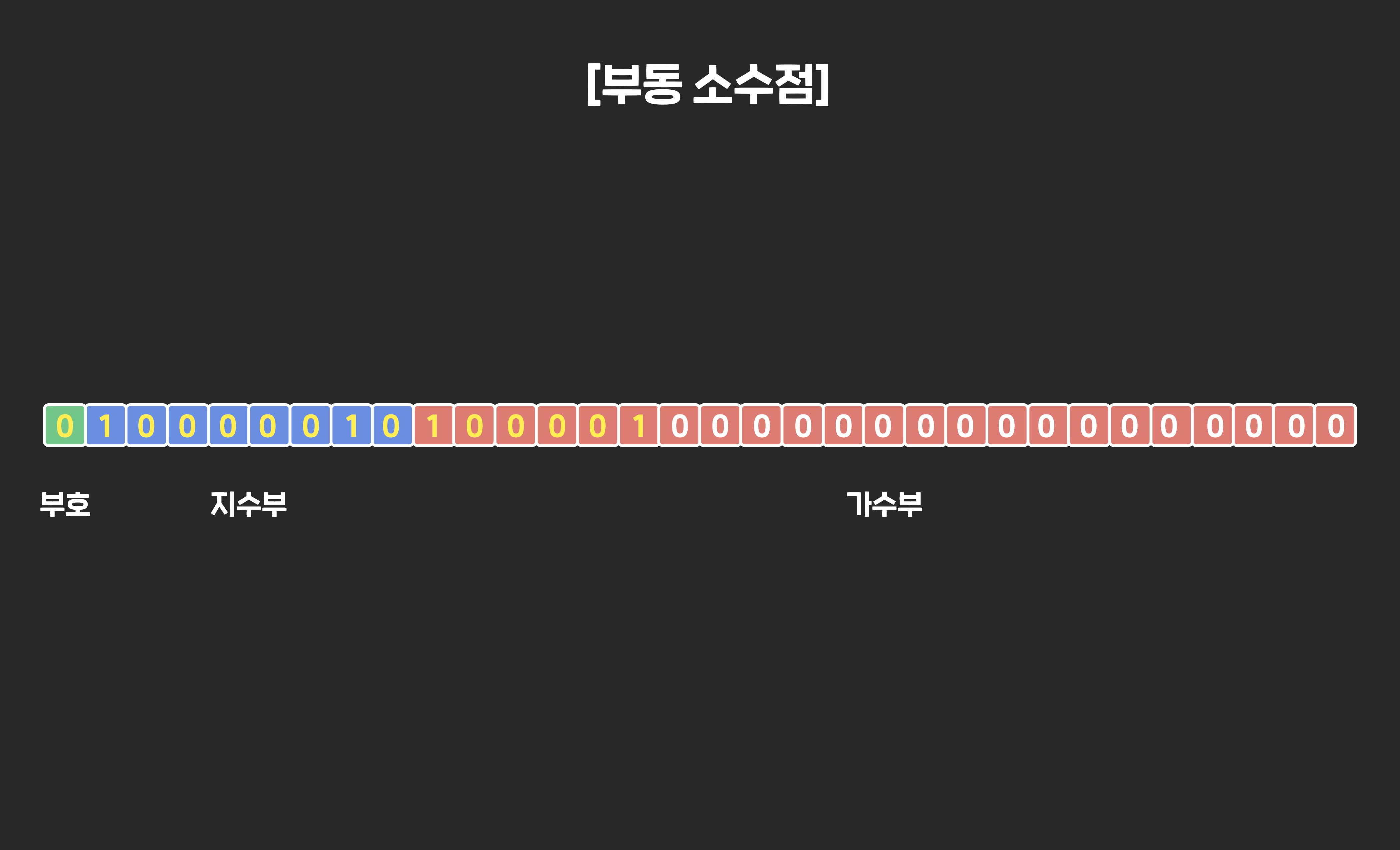
📌 3. 고정 소수점과 부동 소수점의 의의

📎 고정 소수점과 부동 소수점의 의의

부동 소수점 방식을 사용하면 고정 소수점 방식보다 훨씬 더 많은 범위까지 표현할 수 있다. 하지만 부동 소수점 방식에 의한 실수의 표현은 항상 오차가 존재한다는 단점을 가지고 있다.

따라서 컴퓨터에서 실수를 표현하는 방법은 정확한 표현이 아닌 언제나 근사치를 표현할 뿐이다.

📖 참고

코딩하는 포로리

이전 포스트