배열의 인덱스는 0부터 시작한다. 예를 들어
N개의 데이터가 있다면0부터N-1번 인덱스까지 존재한다. 다만, 누적 합을 구현함에 있어 인덱스를1번 인덱스부터 사용하는것이 더 편할 수 있다. 즉,N개의 데이터가 있을경우1번 인덱스부터N+1인덱스까지 사용하는것이다. 아래의 글의 그림에서는0번 인덱스부터 사용하고 있지만 실제로 누적합을 구현할때는1번 인덱스부터 사용하도록 구현할 것!
누적합(Prefix sum)
반복문으로 구간 합을 구할때의 문제점
백준 구간합 구하기4는 문제 이름에서 알 수 있듯이 구간합을 구하는 문제를 살펴보자. 최대 10만개짜리 배열에서 최대 10만번의 i번째부터 j번째 수까지의 합을 출력해야 한다.
N개의 수를 입력받아둔 배열을 A라고 할 때, 단순, 반복문을 사용해서 답을 구하면 최악의 경우 반복문이 N번 돌게 되므로 O(N)의 시간복잡도를 갖게된다. 즉, N과 M모두 최대 10만번이므로 시간 제한인 1초를 아주 많이 넘게된다. (보통 시간복잡도를 계산할 때 1억번의 계산을 1초 정도로 잡는다.)
빠르게 구간합을 구할 수 있는 방법
위에서 반복문으로 구간합을 구할 때의 문제점을 개선하기 위해서는 더 빠른 속도로 구간합을 구할 수 있는 방법을 찾아야한다.
먼저, f(x)를 배열에서 1번째부터 x번째까지의 합이라고 가정해보자. 배열 A의 i번째 수 A[i]를 Ai라고 표현하자. 이를 수식으로 표현하면 아래와 같다.
f(x) = A1 + A2 + ... + Ax그럼 이때 배열 A에서 i번째부터 j번째까지(단, i<=j) 구간의 합을 구하려면 어떻게 해야할까...? 먼저, f(i-1)과 f(j)를 살펴보자.
f(i-1) = A1 + A2 + ... + Ai-1f(j) = A1 + A2 + ... + Ai-1 + Ai + Ai+1 + ... + Aji<=j 이므로 f(j)의 중간에 Ai가 들어가게 된다. 따라서, f(j) - f(i-1)은 i번째부터 j번째까지의 구간 합이 된다.
f(j) - f(i-1) = Ai + Ai+1 + ... + Aj즉, 구간합을 구하기 위해 반복문을 사용했을 떄는 A1 ~ AN까지의 수 모두를 알아야 했고 최악의 경우 N가지를 알아야 했지만 누적합 개념을 이용했을 때는 f(j)와 f(i-1) 두가지만 알면 구할 수 있게 된것이다. 즉, O(N)의 시간복잡도가 걸리던 작업을 O(1)로 줄일 수 있게 된다.
그렇다면 0부터 N-1번째까지의 누적합은 어떻게 구할까?
1부터 N까지의 누적합을 구하는 식은 생각보다 간단하다. 1부터 N까지의 합f(N)은 1부터 N-1까지의 합에 AN을 더한값이다. 수식으로는 아래처럼 표현할 수 있다.
f(N) = f(N-1) + AN이제 실제 코드로 수식을 표현해보자. 배열 A가 있다고 가정해보자. 배열의 요소는 A = {1,3,6,5,10,1} 이다. 그리고 누적합을 나타내는 f(N)을 sum[N]이라고 바꿔서 표현해보자.
int[] sums = new int[N];
for (int i = 1; i < sums.length; i++) {
sums[i] = sums[i - 1] + numbers[i];
}
다음으로, 구간합을 구하는 수식을 코드를 살펴보자. 만약, 4번째 인덱스부터 ~ 5번째 인덱스까지의 합을 구하려는 식을 코드로 작성하면 어떻게 해야할까? (참고로 인덱스는 0부터 시작이다.)
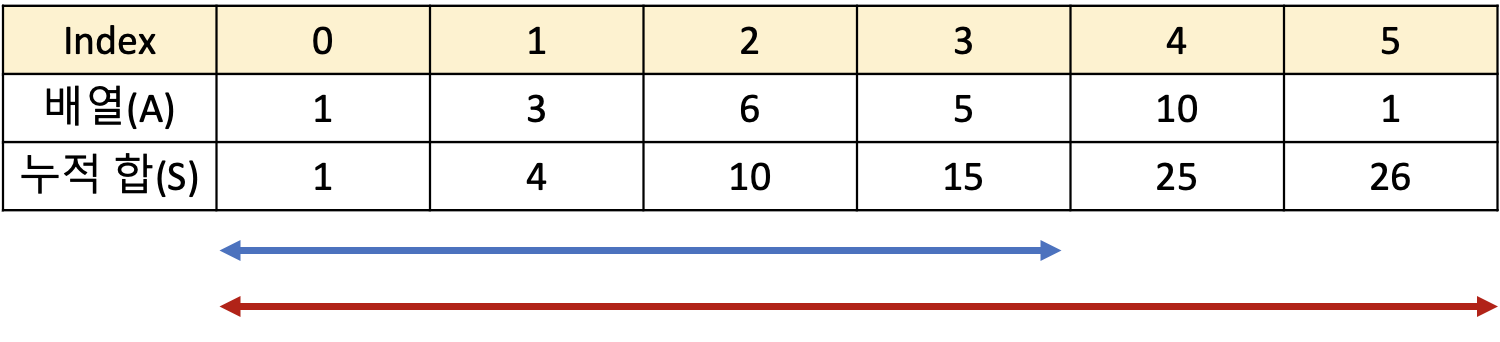
sum[5]는 A0~A5까지의 합이고, 빨간색 화살표로 표현되고 있다. sum[3]은A0~A3까지의 합이고 파란색 화살표로 표현되고 있다. A4~A5은 빨간색 막대에서 파란색 막대를 뺀 부분이다. 즉 A4~A5의 합은 sum[5]-sum[4-1]로 한 번에 구할 수 있다.
int result = sums[5] + sums[4-1];2차원 누적합
2차원 누적합으로 2차원 배열의 구간합을 구해보자.
2차원 배열의 누적합도 1차원 배열의 누적합과 크게 다르지 않다. 1차원 배열에서 sum[N]은 1번째부터 N번째까지의 합을 나타냈다. 그럼 이차원 배열sum[N][M]을 (0,0)부터 (N, M)까지의 합이라고 해보자.
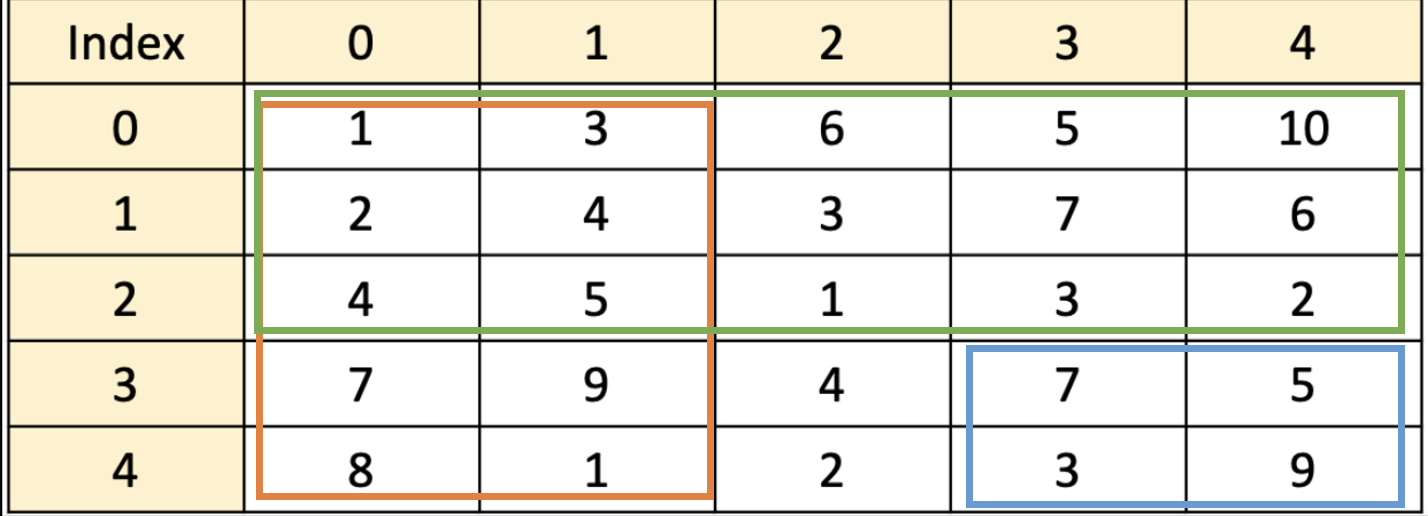
위 그림의 파란색 부분 (3,3)부터 (4,4)의 합을 어떻게 구할 수 있을까? sum[4][4]는 (0,0)부터 (4,4)까지의 합을 나타낸다. 따라서, 전체 누적합인 sum[4][4]에서 주황색과 초록색을 빼주고 마지막으로 두번 빼진 주황색과 초록색이 겹치는 부분(sum[2][2])을 한번 더해주면 된다.
즉, (3,3)부터 (4,4)까지의 2차원 구간합 = sums[4][4] - sums[4][3-1] - sums[3-1][4] + sum[3-1][3-1] 이다. 모든 경우에 적용할 수 있도록 (N1,M1)부터 (N2,M2)까지 (N1<=N2, M1<=M2)라고 가정하고 2차원 배열의 구간합을 수식으로 표현하면 아래와 같다.
sums[N2][M2] - sums[N2][M1-1] - sum[N1-1][M2] + sum[N1-1][M1-1]그럼 (0,0)부터 (N,M)까지의 모든 위치의 값만 유효한 시간내에 구할 수 있따면 그 이후 구간합은 O(1)의 시간복잡도로 구할 수 있게된다.
그럼 (0,0)부터 (N,M)까지의 누적합을 구해보자.
2차원 배열에서 (0,0)부터 (N,M)까지의 누적합을 구하는 방법에 대해 살펴보자. 입력으로 들어온 이차원 배열 A를 살펴보자. 파란색 박스로 되어있는 (2,2)에 해당하는 부분을 구하는 식은 sums[2][2] = sums[2-1][2] + sum[2][2-1] - sums[2-1][2-1] + A[2][2]로 구할 수 있다. 즉, 녹색과 주황색부분을 더하고, 겹치는 부분은 두번 더했으니 한번 빼준다. 마지막으로 현재 값을 더하면 된다.
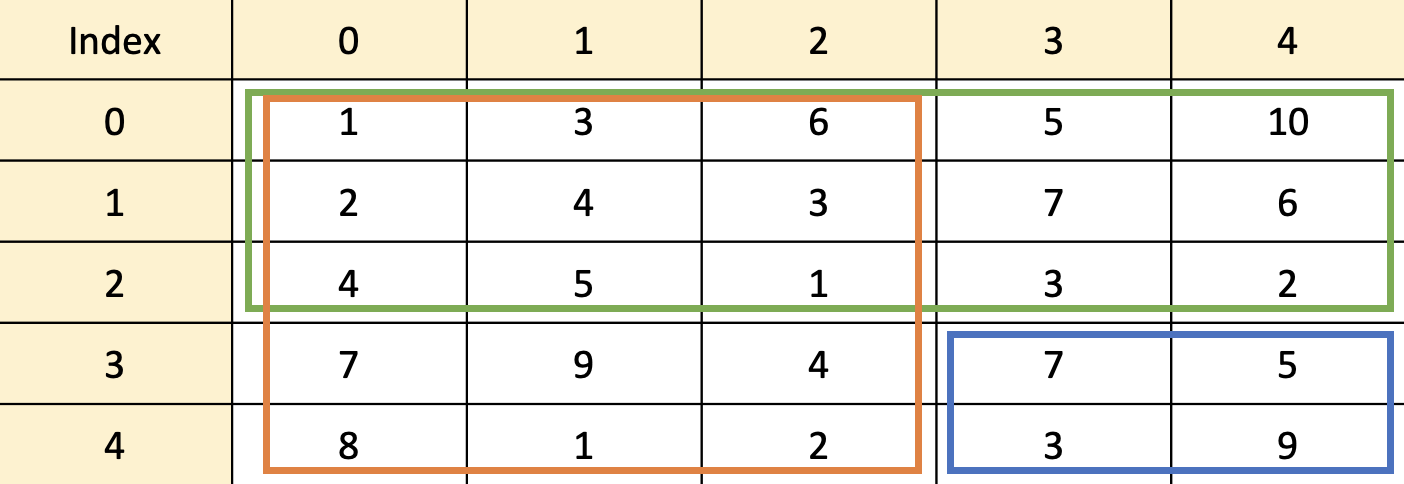
그렇다면 (0,0)부터 (N,M)까지의 배열 A를 입력받았을 때를 기준으로 누적합을 구하는 코드를 작성하면 아래와 같다.
for (int i = 1; i <= length - k; i++) {
for (int j = 1; j <= length - k; j++) {
sum[i][j] = A[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
}
}