[알고리즘] | 위상정렬(Topological Sort)

제롬·2023년 6월 26일

목록 보기

5/6

위상정렬의 개념

방향 그래프에서 정점(vertex)을 간선(edge)의 방향에 거스르지 않도록 나열하는것을 말한다.

위상정렬은 선후 관계가 정의된 그래프 구조상에서 선후 관계에 따른 정렬에 사용될 수 있다. 대표적으로 대학교 수강과목에서 선수과목의 구조를 예를 들 수 있다. 선수과목이 있다면 선수과목을 먼저 수강해야 하기 때문에 특정 과목을 수강해야 할 때 위상정렬을 이용할 수 있다.

[위상정렬 예시 - 선수과목을 고려한 학습순서]

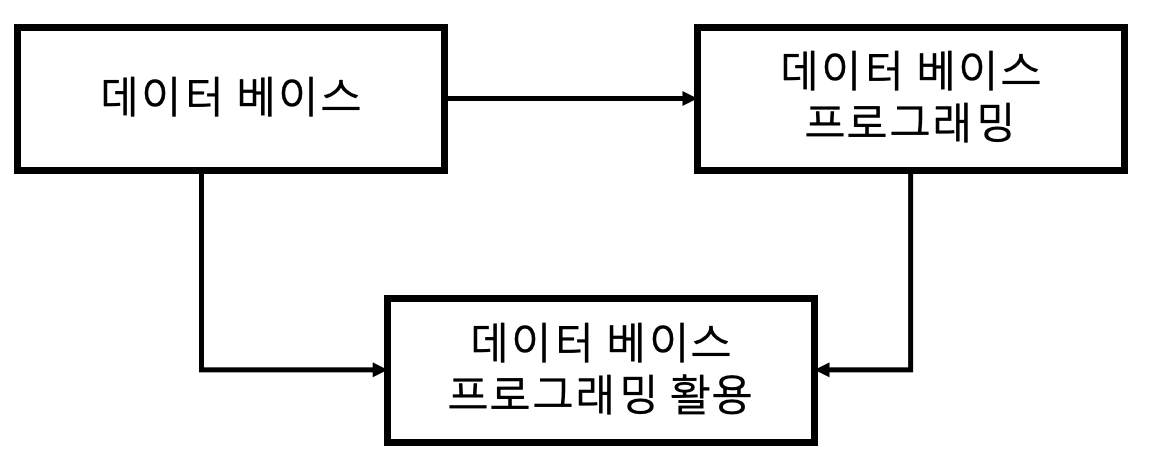
위 그림에서 세 과목을 모두 듣기 위한 적절한 학습순서는?
데이터베이스 -> 데이터베이스 프로그래밍 -> 데이터베이스 프로그래밍 활용

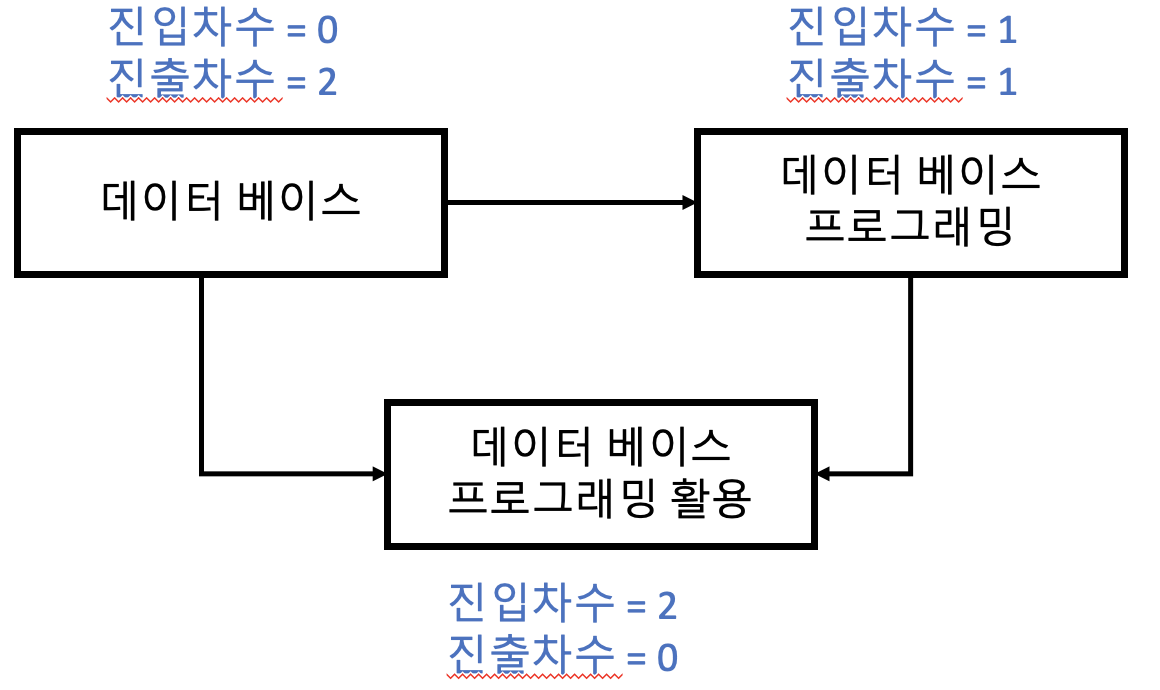
위상정렬 관련 개념 - 진입차수, 진출차수

진입차수(Indegree) : 특정한 노드로 들어오는 간선의 개수
진출차수(Outdegree) : 특정한 노드에서 나가는 간선의 개수

위상정렬 성립조건 및 특징

위상정렬은 순환하지 않는 방향그래프(DAG - Direct Acyclic Graph)에서만 수행할 수 있다.
위상정렬은 구조에 따라 (한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면) 여러가지 답이 존재할 수 있다.
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다. 만약, 사이클이 존재한다면 사이클에 포함된 어떤 원소도 큐에 들어가지 못한다.
스택을 활용한 DFS를 이용해 위상정렬도 수행이 가능하다.

위상정렬 알고리즘 구현방법

큐를 이용하는 위상정렬 알고리즘의 동작과정은 아래와 같다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
- 큐가 빌 때까지 아래의 과정을 반복한다.
  - 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
  - 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.

위상정렬 동작 예시

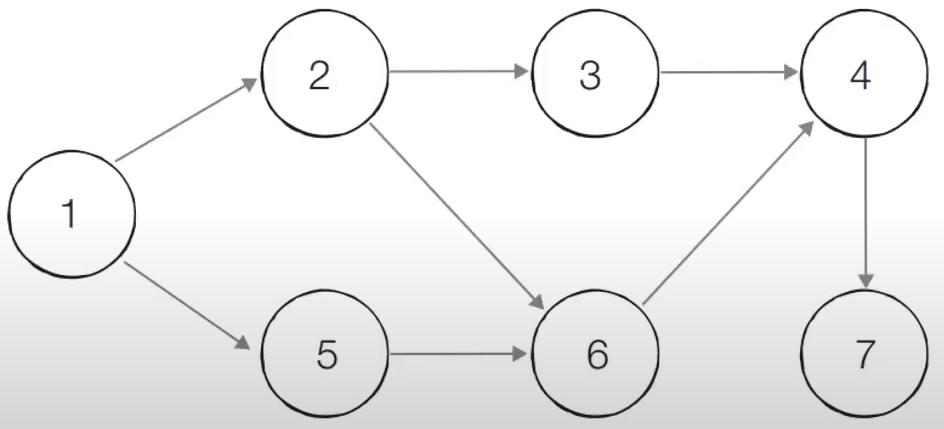
위상정렬을 수행할 그래프를 만든다.
- 이때, 그래프는 사이클이 없는 방향그래프여야 한다.

초기 단계에서는 진입차수가 0인 모든 노드를 큐에 넣는다.
- 처음에 노드1이 큐에 삽입된다.

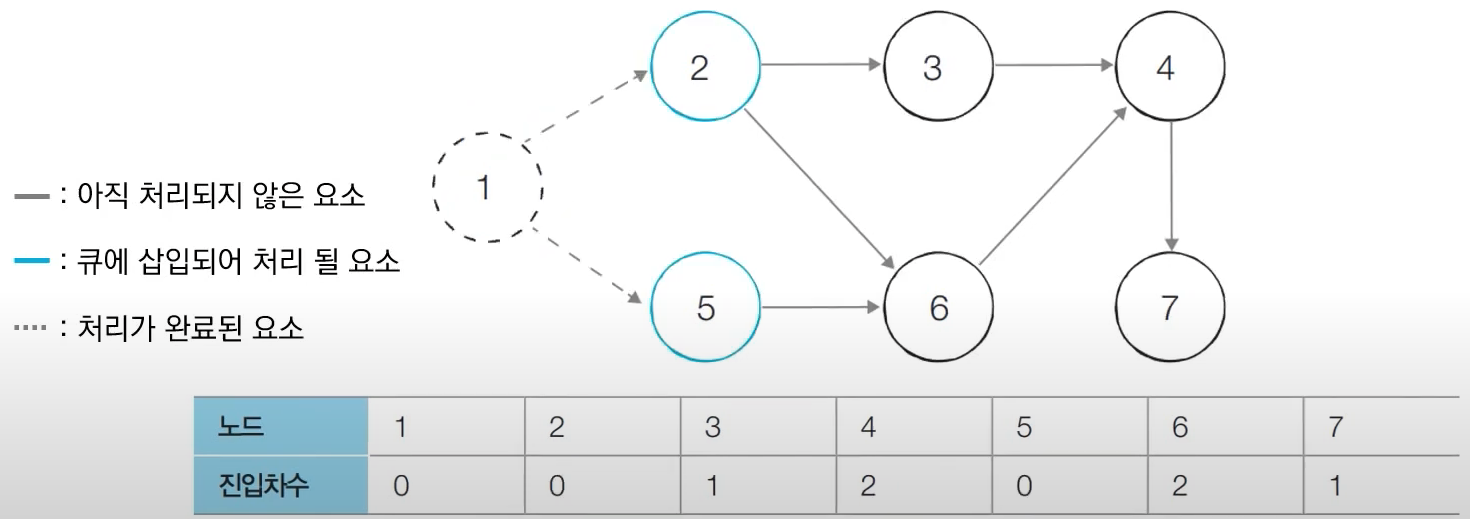
큐에서 노드 1을 꺼낸 뒤에 노드 1에서 나가는 간선을 제거한다.
- 진입차수가 0 이된 노드들을 큐에 삽입한다. -> 노드 2,5

큐에서 노드 2를 꺼낸 뒤에 노드2에서 나가는 간선을 제거한다.
- 진입차수가 0이된 노드를 큐에 삽입한다. -> 노드 3

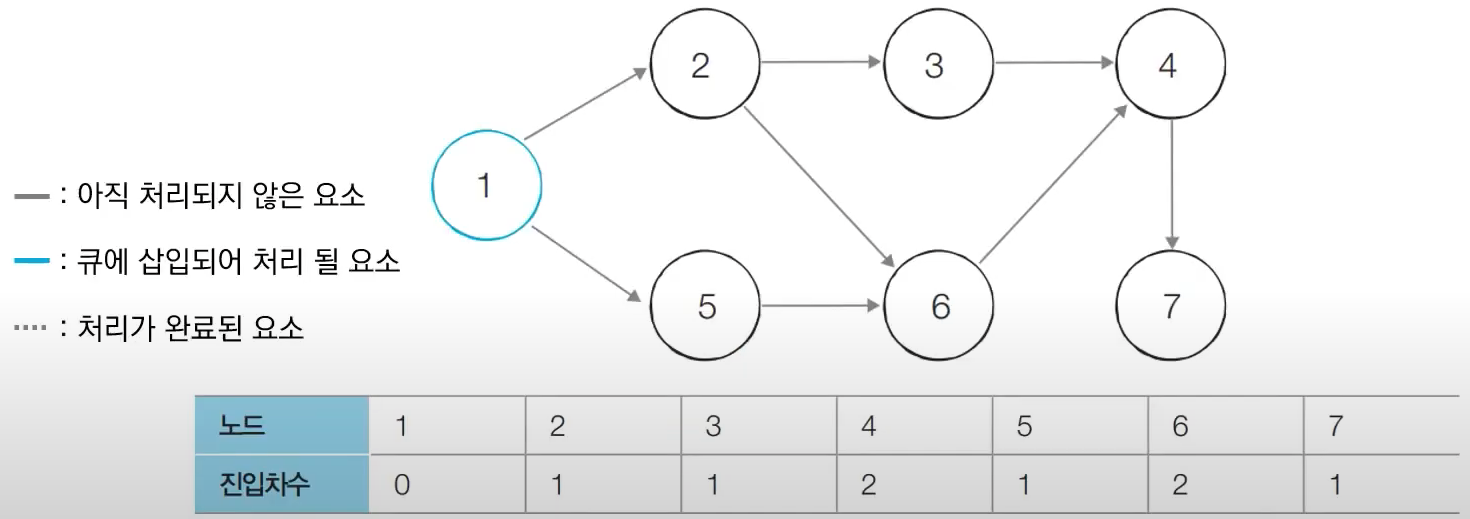
큐에서 노드5를 꺼낸 뒤에 노드5에서 나가는 간선을 제거한다.
- 진입차수가 0이된 노드를 큐에 삽입한다. -> 노드 6

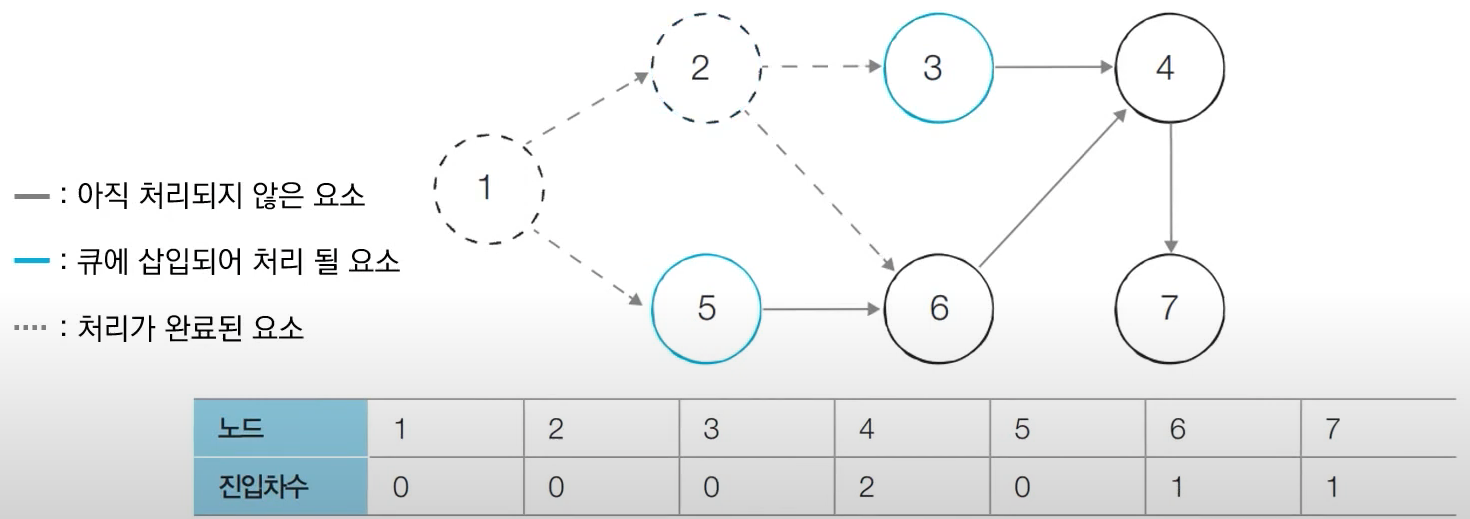
큐에서 노드 6을 꺼내 노드 6에서 나가는 간선을 제거한다.
- 진입차수가 0이된 노드를 큐에 삽입한다. -> 노드 4

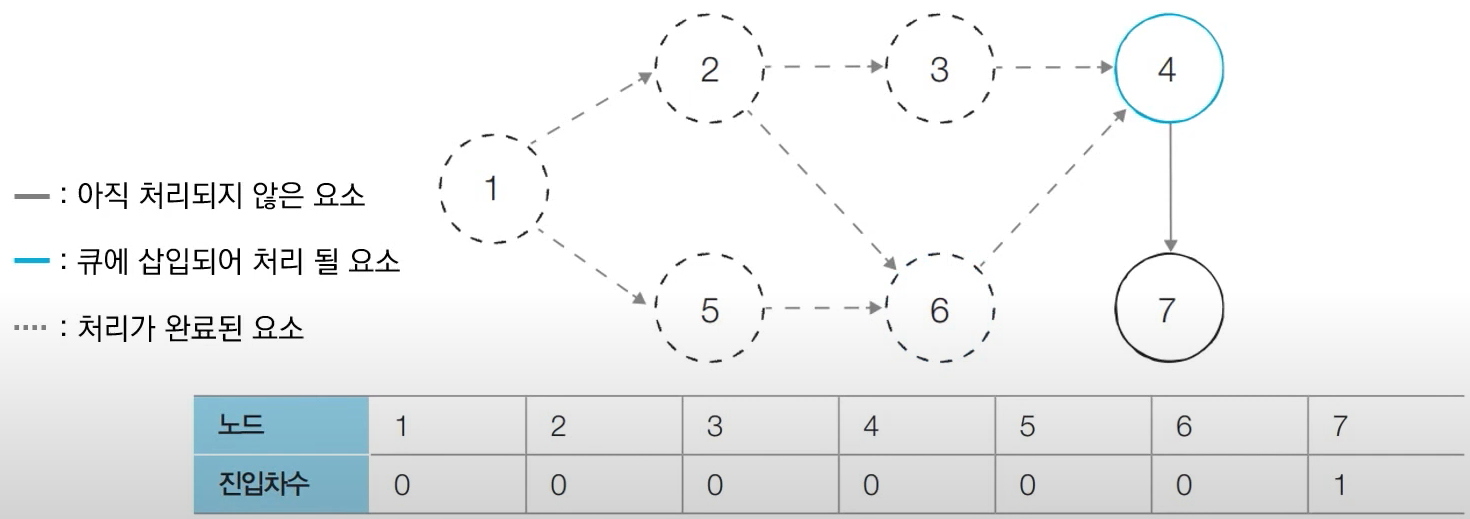
위의 노드에서 간선을 제거하는 작업을 마지막 노드까지 반복하면 더이상 진입차수가 0이된 노드가 없으므로 동작이 종료된다. 큐에 삽입된 전체노드순서가 위상정렬의 결과가 된다. 즉, 위상정렬 동작 수행 결과는 아래와 같다.
[1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7]

위상정렬 알고리즘 코드(java)

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int vertex = sc.nextInt(); // 노드 개수
        int edge = sc.nextInt(); // 간선의 개수
        
        int[] indegree = new int[vertex+1];
        // 모든 노드에 대한 진입차수는 0으로 초기화
        
        List<List<Integer>> graph = new ArrayList<>();
        // 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화

        // 그래프 초기화
        for (int i = 0; i <= v; i++) {
            graph.add(new ArrayList<Integer>());
        }

        // 방향 그래프의 모든 간선 정보를 입력 받기
        for (int i = 0; i < e; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            graph.get(a).add(b); // 정점 A에서 B로 이동 가능
            indegree[b] += 1; // // 진입 차수를 1 증가
        }

        topologySort(vertex, edge, indegree, graph);
    }

    // 위상 정렬 함수
    public static void topologySort(int vertex, int edge, 
    	int[] indegree, List<List<Integer>> graph) {
        
        List<Integer> result = new ArrayList<>(); 
        // 알고리즘 수행 결과를 담을 리스트
        Deque<Integer> queue = new ArrayDeque<>(); 
        // 큐 라이브러리 사용

        // 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
        for (int i = 1; i <= v; i++) {
            if (indegree[i] == 0) {
                queue.offer(i);
            }
        }

        // 큐가 빌 때까지 반복
        while (!queue.isEmpty()) {
            // 큐에서 원소 꺼내기
            int now = queue.poll();
            result.add(now);
            // 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
            for (int i = 0; i < graph.get(now).size(); i++) {
                indegree[graph.get(now).get(i)] -= 1;
                // 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
                if (indegree[graph.get(now).get(i)] == 0) {
                    queue.offer(graph.get(now).get(i));
                }
            }
        }

        // 위상 정렬을 수행한 결과 출력
        for (int i = 0; i < result.size(); i++) {
            System.out.print(result.get(i) + " ");
        }
    }

}