[알고리즘] | 비트마스크

제롬·2022년 4월 14일

알고리즘

목록 보기

4/6

비트마스크란?

컴퓨터는 내부적으로 모든 자료를 이진수(비트)로 처리한다. 이런 컴퓨터의 연산방식을 이용한, 정수의 이진수 표현을 활용하여 문제를 해결하는 기법을 말한다.

비트(Bit)란?

비트는 이진수(0과1로 구성된 수)를 나타내는 말로 컴퓨터에서 사용하는 데이터의 최소 단위이다.
비트는 1과0의 값을 가질 수 있고 true(1) 또는 false(0)라는 상태를 나타낼수도 있다.
우리가 사용하는 10진수는 0과1로 구성된 비트(이진수)로 표현이 가능하다.

비트마스크의 장점

수행시간이 빠르다.
- 대부분의 연산이 O(1)의 시간복잡도를 갖는다.
  - 특정 원소의 존재여부 판단시 선형탐색할 필요없이 and연산결과가 0보다 큰지 검사
코드가 짧다.
- 집합연산들을 비트 연산자로 작성하기 때문에 코드가 간결해 진다.
메모리 사용량이 적다.
- bit가 10개인경우 각 비트는 2가지 경우를 가지기 때문에 2의 10제곱의 경우의 수를 10 bit의 이진수 하나로 표현이 가능하다.

비트 연산

비트연산의 종류
- and(&), or(|), xor(^), not(~)
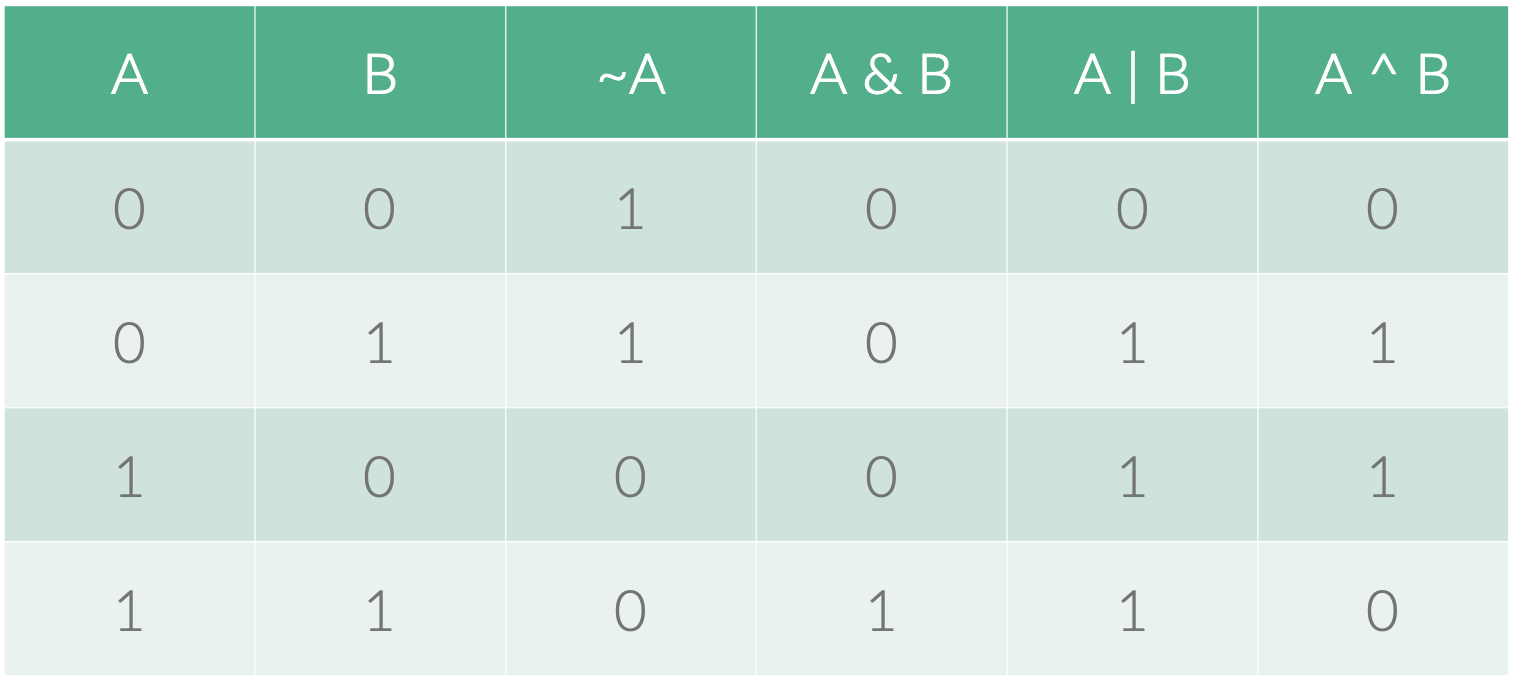
두 수 A,B를 비트 연산하는 경우 가장 뒤의 자리부터 하나씩 연산해주면 된다.

비트 연산 - and 연산(&)

[and 연산 계산과정]

A = 27, B = 83 인 경우, A와 B를 이진수로 표현하면 아래와 같다.
A = 11011, B = 1010011 
이 경우 And 연산을 하면 아래와 같다.
  0 0 1 1 0 1 1
& 1 0 1 0 0 1 1
-----------------
  0 0 1 0 0 1 1 
  
답 : A&B = 19

and 연산의 경우 각 자리수를 비교하여 두 자리가 모두 1일 경우에만 1 하나만 1이거나 둘다 모두 0일경우 0으로 계산한다.
A와 B는 자리수가 다르므로 이를 맞춰주기 위해 A의 앞에 0을 B의 개수에 맞춰 추가해 준다. (자릿수가 적은쪽 앞에 0을 추가)

비트 연산 - or 연산(|)

[or 연산과정]

A = 27, B = 83 인 경우, A와 B를 이진수로 표현하면 아래와 같다.
A = 11011, B = 1010011 
이 경우 And 연산을 하면 아래와 같다.
  0 0 1 1 0 1 1
| 1 0 1 0 0 1 1
-----------------
  1 0 1 1 0 1 1 
  
답 : A|B = 91

and연산과 마찬가지로 A와 B의 자리수를 동일하게 맞춰준다. (자릿수가 적은쪽 앞에 0을 추가)
or 연산은 두 수 중 하나라도 1일 경우 1로 두 숫자 모두 0일경우에만 0으로 계산한다.

비트 연산 - xor 연산(^)

[xor 연산과정]

A = 27, B = 83 인 경우, A와 B를 이진수로 표현하면 아래와 같다.
A = 11011, B = 1010011 
이 경우 And 연산을 하면 아래와 같다.
  0 0 1 1 0 1 1
^ 1 0 1 0 0 1 1
-----------------
  1 0 0 1 0 0 0 
  
답 : A^B = 72

A와 B의 자리수를 동일하게 맞춰준다. (자릿수가 적은쪽 앞에 0을 추가)
xor 연산은 두 수가 다를 경우 즉 0과 1일경우 1 나머지의 경우 0으로 계산한다.

비트 연산 - not 연산(~)

[not 연산과정]

A = 83인 경우, A를 이진수로 표현하면 아래와 같다.
A = 1010011 
이 경우 not 연산을 하면 아래와 같다.

8비트 ~A : 0101100
32비트 ~A : 11111111111111111111111110101100
  
답 : ~A = 72

singed, unsigned에 따라 값이 달라진다.
not연산의 경우 자료형에 따라 값이 달라진다.
not 연산의 경우 비트값을 반전하여 0 -> 1 그리고 1 -> 0 으로 바꾸는 방식으로 계산한다.

비트연산 - shift left 연산(<<)

A << B  
위 식은 A를 B만큼 왼쪽으로 밀어준다 라는 의미를 갖는 식이다. 
밀어준만큼 동시에 0을 추가해준다.

shift left연산의 예를 살펴보자.

1 << 0 -> 1
1 << 1 -> 2 (10)
1 << 2 -> 4 (100)
1 << 3 -> 8 (1000)
1 << 4 -> 16 (10000)
3 << 3 -> 24 (11000)
5 << 10 -> 5120 (1010000000000)

A << B 식은 A * 2의 B제곱과 같다.

비트연산 - shift right 연산(>>)

A >> B  
위 식은 A를 B만큼 오른쪽으로 밀어준다 라는 의미를 갖는 식이다. 
밀어준만큼 동시에 0을 추가해준다.

shift right연산의 예를 살펴보자.

1 >> 0 -> 1
1 >> 1 -> 0 (0)
10 >> 1 -> 5 (101)
10 >> 2 -> 2 (10)
10 >> 3 -> 1 (1)
30 >> 1 -> 15 (1111)
1024 >> 10 -> 1 (1)

A >> B 식은 A / 2의 B제곱과 같다.

비트마스크를 이용한 집합의 표현

비트마스크를 이용해 정수로 집합을 표현할 수 있다.
비트가 1(true)이면 해당 원소가 존재한다는 의미이고 비트가 0(false)이면 해당 원소가 존재하지 않는다는 의미이다.
N비트 정수 변수라면 N개의 원소를 갖는 집합의 부분집합들을 모두 표현할 수 있다.
원래는 N개의 원소를 갖는 boolean 배열을 선언해야 했지만 비트마스크를 이용하면 하나의 정수로 표현이 가능하기 때문에 사용하는 메모리의 크기가 굉장히 줄어든다.

[비트마스크를 이요한 정수 집합 표현]
예를 들어 [1, 3, 4, 5, 9]라는 집합이 있다고 생각해보면, 아래 그림처럼 비트로 표현이 가능하다.

10까지의 원소중 [1, 3, 4, 5, 9]에 해당하는 원소만 집합에 존재하므로 해당 번호에 해당하는 원소값만 1로 표현해주었다.

따라서 [1, 3, 4, 5, 9] = 570의 정수로 표현이 가능하다.

즉, 원소의 개수가 N인 집합이 있다고 가정하면, 각 원소의 번호는 0부터 N-1까지 부여가 가능하다.

또한 각 번호에 해당하는 원소가 존재하면 비트가 1, 존재하지 않으면 비트는 0으로 표현이 가능하다.

비트마스크를 이용한 집합연산 - 원소 포함여부 검사

K 번째 원소가 포함되었는지 여부를 확인하고 싶다면 and 연산을 이용해서 K번째 비트가 1인지 여부만 확인하면 된다.

집합A = [1, 3, 4, 5, 9] = 570

2번째 원소가 포함되었는지 여부 확인 => A & (1 << 2)
2번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 and(&)연산의 계산값이 0이 아니라면 2번째 원소의 값은 존재한다는 것을 알 수 있다.

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 0 1 0 0 
-------------------
0 0 0 0 0 0 0 0 0 0

3번째 원소가 포함되었는지 여부 확인 => A & (1 << 3)
3번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 and(&)연산의 계산값이 0이 아니라면 3번째 원소의 값은 존재한다는 것을 알 수 있다.

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 1 0 0 0 
-------------------
0 0 0 0 0 0 1 0 0 0

결과가 1 이므로 해당 원소는 존재한다는 사실을 알 수 있다.
k번째 원소 포함여부 검사 공식은 A & (1 << k)

int x = 32;
System.out.println("4번째 원소 검사: " + Integer.toBinaryString(x & (1 << 3)));

//실행결과
4번째 원소 검사: 1000

비트마스크를 이용한 집합연산 - 원소 추가

A집합에 특정 원소를 추가하는 방법이다. 원소에 해당하는 bit만 1로 바꾸어주면 된다. 때문에 해당 bit를 항상 1로 만드는 연산이 필요하므로 or연산을 이용한다.
단, 이미 해당원소가 존재하는경우 아무런 변화가 없다.

집합A = [1, 3, 4, 5, 9] = 570

2번째 원소 추가 => A | (1 << 2)
2번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 or(|)연산의 계산값이 무조건 1이 나오므로 2번째 원소의 값이 추가됨을 알 수 있다.

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 0 1 0 0 
-------------------
1 0 0 0 1 1 1 1 1 0

3번째 원소가 포함되었는지 여부 확인 => A | (1 << 3)
3번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 or(|)연산의 계산값 무조건 1이 나오므로 3번째 원소의 값이 추가됨을 알 수 있다.

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 1 0 0 0 
-------------------
1 0 0 0 1 1 1 0 1 0

기존 값이 무엇이든 결과가 1 이므로 해당 원소가 추가되었다는 사실을 알 수 있다.

int x = 32;
System.out.println("4번째 원소 추가: " + Integer.toBinaryString(x |= (1 << 3)));

//실행결과
4번째 원소 추가: 101000

비트마스크를 이용한 집합연산 - 원소 삭제

A집합에 특정 원소를 삭제하는 방법이다. 원소에 해당하는 bit만 0로 바꾸어주면 된다. 때문에 해당 bit를 항상 0로 만드는 연산이 필요하므로 and연산을 이용한다.
단, 이미 해당원소가 존재하는 경우에만 가능하다. 만약, 해당원소가 존재하지 않으면 다른 원소의 포함 여부까지 변경될 수 있기 때문이다.

집합A = [1, 3, 4, 5, 9] = 570

2번째 원소 삭제 => A & ~(1 << 2)
(1<<2) 연산을 수행하면 2번째 비트의 위치에만 0이 있고 나머지 비트의 값은 모두 1이다.
여기에 not 연산을 수행하면 2번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 and(&)연산을 수행하면 2번째 원소의 값만 0으로 변한다. 

1 0 0 0 1 1 1 0 1 0
1 1 1 1 1 1 1 0 1 1 
-------------------
1 0 0 0 1 1 1 0 1 0

3번째 원소가 포함되었는지 여부 확인 => A | (1 << 3)
여기에 not 연산을 수행하면 3번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 and(&)연산을 수행하면 3번째 원소의 값만 0으로 변한다. 

1 0 0 0 1 1 1 0 1 0
1 1 1 1 1 1 0 1 1 1 
-------------------
1 0 0 0 1 1 0 0 1 0

1 << k 는 k번째 비트만 켜진 상태이므로 여기에 not연산을 하면 k번째 비트만 꺼진 상태가 된다. 이 값을 활용해 and연산을 수행하면 k번째 비트만 0이되고 나머지 bit는 변하지 않는다.

int x = 32;
System.out.println("4번째 원소 삭제: " + Integer.toBinaryString(x &= ~(1 << 3)));

//실행결과
4번째 원소 삭제: 100000

비트마스크를 이용한 집합연산 - 원소 토글

A집합에 특정 원소가 존재하면 삭제하고, 존재하지 않는다면 추가하는 방법이다.
xor연산을 이용한다.

집합A = [1, 3, 4, 5, 9] = 570

2번째 원소 토글 => A ^ (1 << 2)
(1<<2) 연산을 수행하면 2번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 xor(^)연산을 수행하면 2번째 원소의 값이 반대값으로 바뀐다. (0 -> 1 , 1 -> 0)

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 0 1 0 0 
-------------------
1 0 0 0 1 1 1 1 1 0

3번째 원소가 토글 => A ^ (1 << 3)
(1<<3) 연산을 수행하면 3번째 비트의 위치에만 1이 있고 나머지 비트의 값은 모두 0이다.
이 값에 집합A와 xor(^)연산을 수행하면 3번째 원소의 값이 반대값으로 바뀐다. (0 -> 1 , 1 -> 0)

1 0 0 0 1 1 1 0 1 0
0 0 0 0 0 0 1 0 0 0 
-------------------
1 0 0 0 1 1 0 0 1 0

int x = 32;
System.out.println("4번째 원소 토글: " + Integer.toBinaryString(x ^ (1 << 3)));

// 실행결과
4번째 원소 토글: 101000

비트마스크를 이용한 집합연산 - 전체집합과 공집합

전체집합 : (1 << N) - 1
N의 개수만큼 모든 비트값이 1이다.
인덱스로 바꾸어 계산하기 때문에 -1을 해준다.
공집합 : 0
공집합은 모든 비트가 0이다.

int fullSetA = (1 << 5) - 1;
System.out.println("꽉찬 집합: " + Integer.toBinaryString(fullSetA));

int fullSetALong = -1;
System.out.println("32비트 꽉찬 집합: " + Integer.toBinaryString(fullSetALong));

// 실행결과
8비트 꽉찬 집합: 11111
32비트 꽉찬 집합: 11111111111111111111111111111111

비트마스크를 이용한 두 집합 사이의 연산

A와 B의 합집합 : A | B
A와 B의 교집합 : A & B
A에서 B를 뺀 차집합 : A & (~B)
A와 B중 하나에만 포함된 원소들의 집합 : A ^ B

int a = 38;
int b = 33;

System.out.println("a: " + Integer.toBinaryString(a));
System.out.println("b: " + Integer.toBinaryString(b));

System.out.println("a와 b의 합집합: " + Integer.toBinaryString(a | b));
System.out.println("a와 b의 교집합: " + Integer.toBinaryString(a & b));
System.out.println("a와 b의 차집합: " + Integer.toBinaryString(a & -b));
System.out.println("a와 b의 둘중에 하나만 포함집합: " + Integer.toBinaryString(a ^ b));

// 실행결과
a: 100110
b: 100001
a와 b의 합집합: 100111
a와 b의 교집합: 100000
a와 b의 차집합: 110
a와 b의 둘중에 하나만 포함집합: 111

비트마스크를 이용한 기타 집합 연산

집합 내 존재하는 원소의 개수 : Integer.bitCount(A)
존재하는 원소 중 가장 작은 원소찾기 : int min = A & (-A)
- ~A + 1 : 컴퓨터가 표현하는 A의 2의 보수 (-A)
- 비트 A가 있다고하자.
  가장 오른쪽에 켜져있는 bit를 k라고 하면, 0~k-1의 bit는 모두 0이다.
  그렇다면 ~A에서는 k번째 bit는 0, 0~k-1의 bit는 모두 1이다.
  ~A + 1을 하게 되면 k번째 bit는 1, 0~k-1의 bit는 모두 0이 된다.
  k이후의 비트는 아무 변화가 없다.
  → 따라서, -A와 A를 AND연산을 시키면 k번째 bit만 켜진 상태로 남게 된다.

int first = A & (-A); 
A : 1010,
~A+1 (-A) : 0110,
A&(-A) : 0010

존재하는 원소 중 가장 작은 원소 지우기 : A &= (A-1)
- 가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND시키면 된다. A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.

ex) A &= (A-1);
A : 1010,
A-1 : 1001,
A&(A-1) : 1000

제롬

다음 포스트