7.5 스케일링과 범주형 변수
1. 용어 정리
- 스케일링(scaling): 데이터의 범위를 늘리거나 줄이는 방식으로 여러 변수들이 같은 스케일이 오도록 하는 것
- 정규화(normalization): 원래 변수 값에서 평균을 뺀 후에 표준편차로 나누는 방법으로, 스케일리의 일종이다.
- 고워 거리(Gower's distance): 수치형과 범주형 데이터가 섞여 있는 경우에 모든 변수가 0~1 사이로 오도록 하는 스케일링 방법
7.5.1 변수 스케일링
- Z 정규화

스케일링은 PCA에서도 역시 중요하다. z 점수를 사용하는 것은 주성분을 계산할 때 공분산 행렬 대신 상관행렬을 사용하는 것과 같은 결과를 가져온다. PCA를 계산하는 소프트웨어에는 일반적으로 상관행렬을 사용할 수 있는 옵션이 있다.
7.5.2 지배 변수
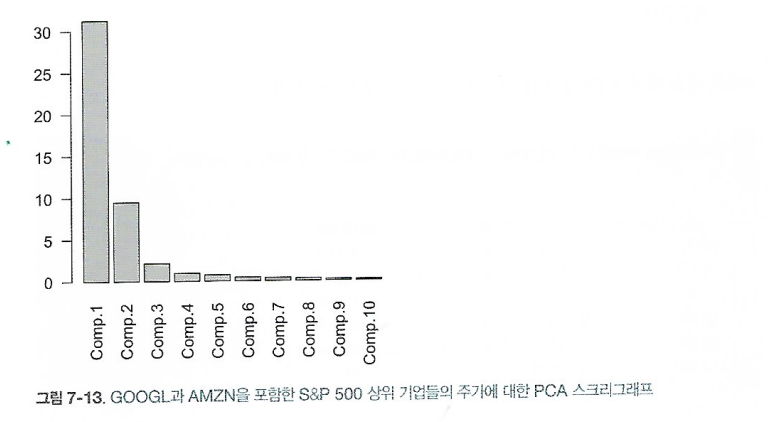
처음 두 가지 주성분은 GOOGL과 AMZN에 의해 완전히 지배되고 있다. 이는 GOOGL 과 AMZN의 주가 움직임이 전체 변동성의 대부분을 지배하기 때문이다.
이러한 상황에서는 변수를 스케일링해서 포함하거나, 이러한 지배변수를 전테 분석에서 제외하고 별도로 처리할 수도 있다.
어떤 방법이 항상 옳다고는 할 수 없으며 응용분야에 따라 달라진다.
7.5.3 범주형 데이터와 고워 거리
1. 들어가며
- 범주형 데이터가 있는 경우에는 순서형 변수 또는 이진형 변수를 사용하여 수치형 데이터로 변환해야 한다.
- 데이터를 구성하는 변수들에 연속형과 이진형 변수가 섞여 있는 경우에는 비슷한 스케일이 되도록 변수의 크기를 조정해야 한다. 이때 고워 거리를 사용한다.
2. 고워 거리의 기본 아이디어
- 수치형 변수나 순서형 요소에서 두 레코드 간의 거리는 차이의 절댓값(맨해튼 거리)으로 계산한다.
- 범주형 변수의 경우 두 레코드 사이의 범주가 서로 다르면 거리가 1이고 범주가 동일하면 거리는 0이다.
3. 고워 거리 계산 방법
- 각 레코드의 변수 i와 j의 모든 쌍에 대해 거리 d를 계산한다.
- 각 d의 크기를 최솟값이 0이고 최댓값이 1이 되도록 스케일을 조정한다.
- 거리 행렬을 구하기 위해 변수 간에 스케일된 거리를 모두 더한 후 평균 혹은 가중평균을 계산한다.
피터 브루스, 앤드루 브루스의 <데이터 과학을 위한 통계(2판): 데이터 분석에서 머신러닝까지 50가지 핵심 개념> 을 읽고 정리한 내용입니다.
