재표본 추출 & 통계적 유의성 & p값

정다영·2022년 8월 18일

데이터 과학을 위한 통계 통계학

데이터 과학을 위한 통계

목록 보기

14/23

3.3 재표본추출

1. 용어 정리

재표본추출: 관측 데이터로부터 반복해서 표본 추출하는 과정.
순열검정(permutation test): 두 개 이상의 표본을 함께 결합하여 관측값들을 무작위로(또는 전부를) 재표본으로 추출하는 과정을 말한다.
복원/비복원(with or without replacement): 표본을 추출할 때, 이미 한 번 뽑은 데이터를 다음번 추출을 위해 다시 제자리에 돌려 놓거나/다음 추출에서 제외하는 표본추출 방법

2. 재표본 추출이란

랜덤한 변동성을 알아보자는 일반적인 목표를 가진다.
관찰된 데이터의 값에서 표본을 반복적으로 추출하는 것을 의미
부트스트랩과 순열검정이라는 두 가지 주요 유형이 있다.

3.3.1 순열검정

1. 순열 검정 절차

a. 여러 그룹의 결과를 단일 데이터 집합으로 결합한다.
b. 결합된 데이터를 잘 섞은 후, 그룹 A와 동일한 크기의 표본을 무작위로(비복원) 추출한다.
c. 나머지 데이터에서 그룹 B와 동일한 크기의 샘플 무작위로(비복원) 추출한다.
d. C, D 등의 그룹에 대해서도 동일한 작업을 수행한다. 아제 원본 표본의 크기를 반영하는 재표본을 수집했다.
e. 원래 샘플(예를 들면 그룹 비율의 차이)에 대해 구한 통계량 또는 추정치가 무엇이었든간에 지금 추출한 재표본에 대해 모두 다시 계산하고 기록한다. 이것으로 한 번의 순열 반복이 진행된다.
f. 앞선 단계들을 R번 반복하여 검정 통계량의 순열 분포를 얻는다.

2. 결론

순열과정에서 얻은 집합에서의 관찰된 차이가 대부분의 순열 분포 바깥에 있다면, 이것은 우연이 아니라고 결론 내릴 수 있다.
이 차이는 통계쩍으로 유의미하다.

3.3.2 예제: 웹 점착성

상대적으로 고가의 서비스를 제공하는 한 회사에서 두 가지 웹 디자인을 놓고 어느 쪽이 더 나은 판매 효과를 가져올지를 검증하려고 한다. 판매되는 서비스가 고가이다 보니 판매가 자주있지 않으며 판매 주기가 상당히 길다. 실제 매출 데이터를 충분히 얻는 데는 너무 오랜 시간이 걸려, 이를 통해 디자인의 우수성을 검증하기가 어렵다. 이런 이유로 이 회사는 서비스를 상세히 설명하는 내부 페이지의 이용을 대리변수로 사용하여 그 결과를 측정하기로 결정한다.

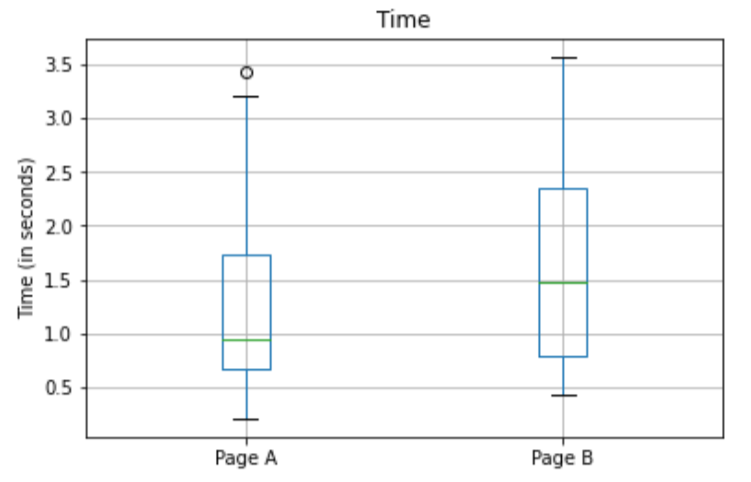
1. 웹 페이지 A와 B의 세션 시간

코드

import pandas as pd
import matplotlib.pyplot as plt

url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/web_page_data.csv"
session_times = pd.read_csv(url)    

ax = session_times.boxplot(by = 'Page', column = 'Time')
ax.set_xlabel('')
ax.set_ylabel('Time (in seconds)')
plt.suptitle('')

결과

2. 각 그룹의 평균 계산

코드

import pandas as pd

url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/web_page_data.csv"
session_times = pd.read_csv(url)    

mean_a = session_times[session_times.Page == 'Page A'].Time.mean()
mean_b = session_times[session_times.Page == 'Page B'].Time.mean()
mean_b - mean_a

결과

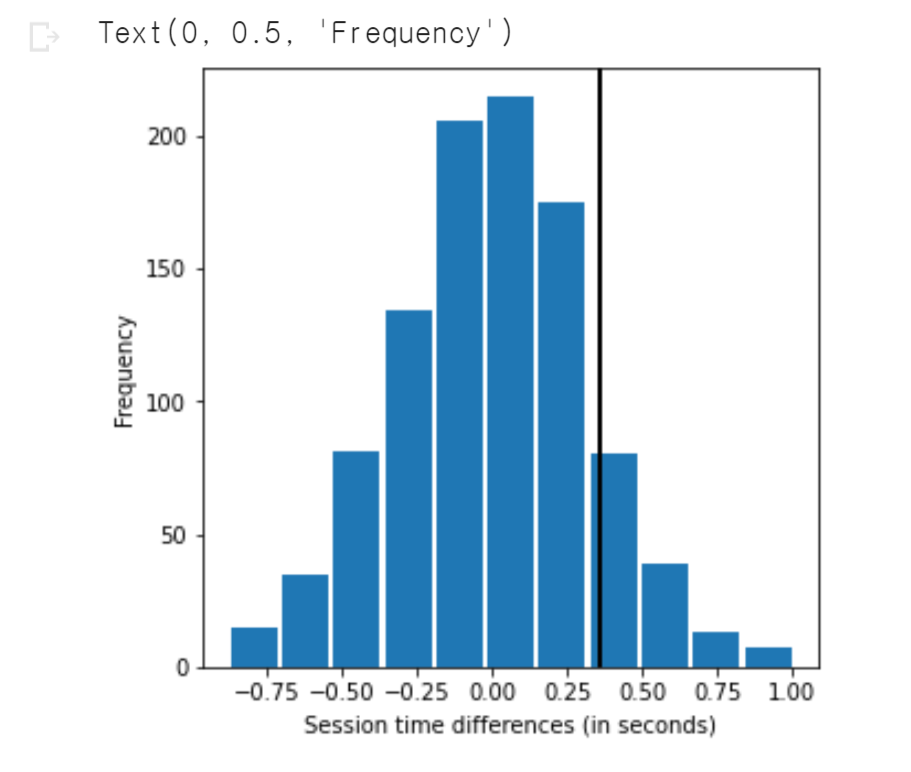
3. 순열 겸정을 이용한 세션 시간의 차이에 대한 도수 분포

코드

import random
import pandas as pd
import matplotlib.pyplot as plt

url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/web_page_data.csv"
session_times = pd.read_csv(url)    


def perm_fun(x, nA, nB):
  n = nA + nB
  idx_B = set(random.sample(range(n), nB))
  idx_A = set(range(n)) - idx_B
  return x.loc[idx_B].mean() - x.loc[idx_A].mean()
  
nA = 21
nB = 15

perm_diffs = [perm_fun(session_times.Time, nA, nB) for _ in range(1000)]

fig, ax = plt.subplots(figsize = (5, 5))
ax.hist(perm_diffs, bins = 11, rwidth = 0.9)
ax.axvline(x = mean_b - mean_a, color = 'black', lw = 2)
ax.text(5, 19, 'Observed\ndifference', bbox = {'facecolor':'white'})
ax.set_xlabel('Session time differences (in seconds)')
ax.set_ylabel('Frequency')

결과

4. 새션 시간의 차이가 확률분포의 범위 내에 있음을 확인
*코드

import numpy as np

np.mean(np.array(perm_diffs) > mean_b - mean_a)

*결과

3.3.3 전체 및 부트스트랩 순열검정

1. 순열 검정의 변종

전체순열검정(exhaustive permutation test)

데이터를 부작위로 섞고 나누는 대신 실제로 나눌 수 있는 모든 가능한 조합을 찾는다.
부트스트랩 순열검정(bootstrap permutation test)

무작위 순열검정의 2단계와 3단계에서 비복원으로 하던 것을 복원 추출로 수행한다.

3.3.4 순열검정: 데이터 과학의 최종 결론

순열 검정에서는 여러 표본을 결합한 다음 잘 섞는다.
그런 다음 섞인 값들을 이용해 재표본추출 과정을 거쳐, 관심 있는 표본 통계량을 계산한다.
이 과정을 반복하고 재표본추출한 통계를 도표화한다.
관측된 통계량을 재표본추출한 분포와 비교하면 샘플 간에 관찰된 차이가 우연에 의한 것인지를 판단할 수 있다.

3.4 통계적 유의성과 p값

1. 용어 정리

p값(p-value): 귀무가성을 구체화한 기회 모델이 주어졌을 때 관측된 결과와 같이 특이하거나 극단적인 결과를 얻을 확률
알파(alpha): 실제 결과가 통계적으로 의미 있는 것으로 간주되기 위해, 우연에 의한 결과가 능가해야하는 '비정상적인' 가능성의 임계 확률
제 1종 오류(type 1 error): 우연에 의한 효과를 실제 효과라고 잘못 결론 내리는 것
제 2종 오류(type 2 error): 실제 효과를 우연에 의한 효과라고 잘못 결론 내리는 것

2. '두 가격이 동일한 전환율을 공유하는지, 이 랜덤 변이가 5%만큼의 차이를 만들어낼 수 있는지'에 대한 순열 절차

a. 0과 1이 적힌 카드를 박스에 넣는다. 그러면 전체 전환률은 45,945개의 0과 382개의 1이므로 0.00826 = 0.8246% 라고 할 수 있다.
크기 23,739(가격 A)의 표본을 섞어서 뽑고 그중 1이 몇 개인지 기록하자.
나머지 22,588개(가격 B)에서 1의 수를 기록하자.
1의 비율 차이를 기록하자.
2~4단계를 반복한다.
이 차이가 얼마나 자주 >= 0.0368인가?

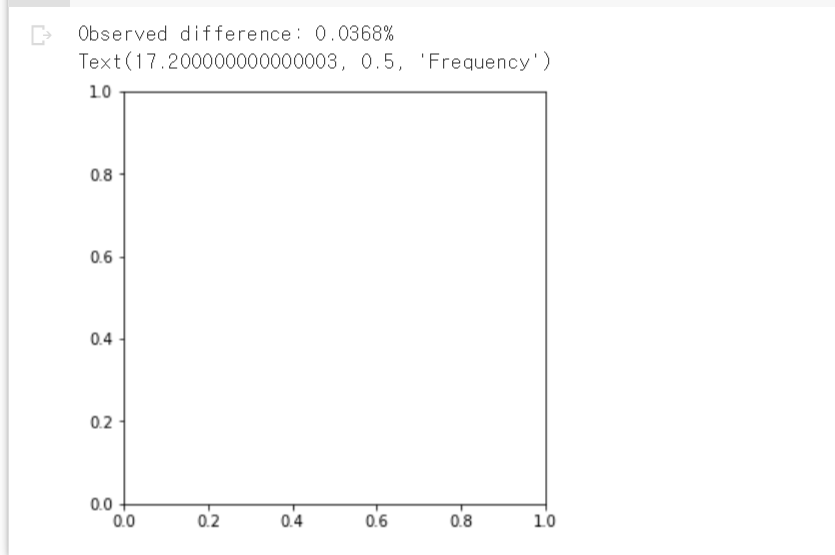
3. 예제: 전환율 차이에 대한 도수 분포

코드

import pandas as pd
import matplotlib.pyplot as plt

def perm_fun(x, nA, nB):
  n = nA + nB
  idx_B = set(random.sample(range(n), nB))
  idx_A = set(range(n)) - idx_B
  return x.loc[idx_B].mean() - x.loc[idx_A].mean()


obs_pct_diff = 100 * (200 / 23739 - 182 / 22588)
print(f'Observed difference: {obs_pct_diff:.4f}%')
conversion = [0] * 45945
conversion.extend([1] * 382)
conversion = pd.Series(conversion)

perm_diffs = [100 * perm_fun(conversion, 23739, 22588) for _ in range(1000)]

fig.ax = plt.subplots(figsize = (5, 5))
ax.hist(perm_diffs, bins = 11, rwidth = 0.9)
ax.axvline(x = obs_pct_diff, color = 'black', lw = 2)
ax.text(0.06, 200, 'Observed\ndifference', bbox = {'facecolor' : 'white'})
ax.set_xlabel('Conversion rate (percent)')
ax.set_ylabel('Frequency')

결과
결과가 왜 안나올까

3.4.1 p값

1. p값

통계적 유의성을 특정하기 위한 지표
코드

import numpy as np

np.mean([diff > obs_pct_diff for diff in perm_diffs])

결과

2. 정규 근사법 이용

코드

import scipy.stats as stats
import numpy as np

survivors = np.array([[200, 23739 - 200], [182, 22588 - 182]])
chi2, p_value, df, _ = stats.chi2_contingency(survivors)

print(f'p-value for single sided test: {p_value / 2:.4f}')