Recursion

정의

• 함수가 자기 자신을 호출하는 것
• Tree구조를 다루는데 유용함

예시

• 팩토리얼 계산의 예시 : n 팩토리얼을 계산하는 과정에서 n-1 팩토리얼의 계산 과정을 필요로 함

  	n! = (n = 0) 1 || (n >= 1) n * (n-1)!

• 자기 자신을 호출하기 때문에 정지 조건을 명시하지 않으면 무한히 반복하게 됨

재귀 연산 과정

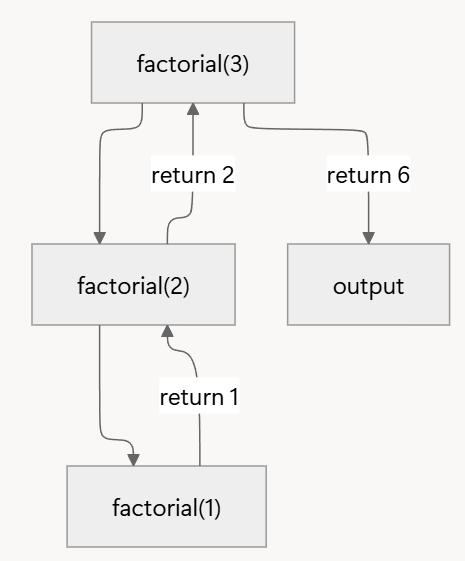
• factorial(3)을 연산하는 과정을 통해 재귀 연산 과정을 알아봄
  

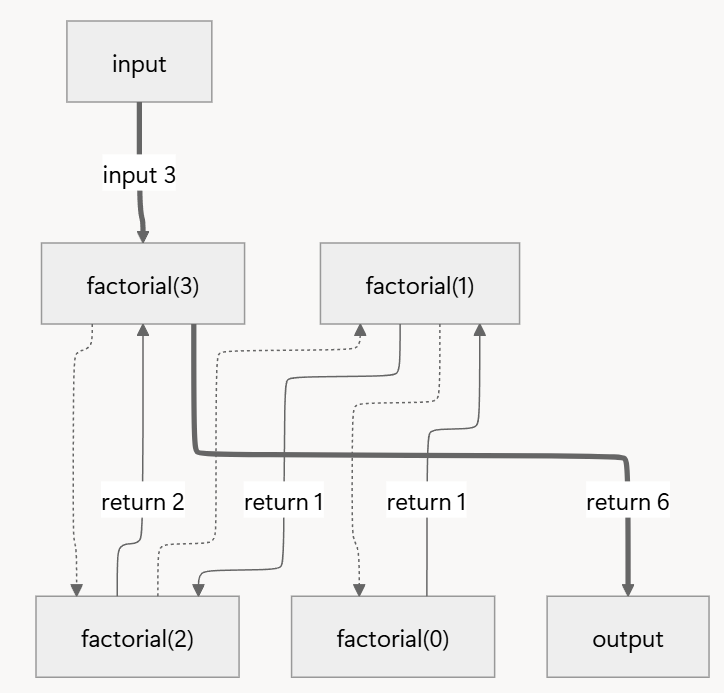
1. factorial(3)에서 종료 조건 검사
   → 3 == 0 이 false이므로 3 * factorial(3-1) 연산 과정에서 factorial(2) 호출
2. factorial(2)에서 종료 조건 검사
   → 2 == 0 이 false이므로 2 * factorial(2-1) 연산 과정에서 factorial(2) 호출
3. factorial(1)에서 종료 조건 검사
   → 1 == 0 이 false이므로 1 * factorial(1-1) 연산 과정에서 factorial(0) 호출
4. factorial(0)에서 종료 조건 검사
   → 0 == 0 이 true이므로 1을 반환
5. factorial(0)이 1을 반환, factorial(1) 함수에서 1 * factorial(0)의 값이 1로 도출되어 반환됨
6. factorial(1)이 1을 반환, factorial(2) 함수에서 2 * factorial(1)의 값이 2로 도출되어 반환됨
7. factorial(2)의 값이 3을 반환, factorial(3) 함수에서 3 * factorial(2)의 값이 6으로 도출되어 최종적으로 값을 출력

구성

• 자기 자신을 호출하는 재귀 파트
• 종료 조건을 포함하는 종료 파트

예시

• 재귀 방식은 Divide and Conquer 방식을 기본적으로 사용하며 특정 작업을 작은 부분으로 쪼갠 뒤 각각을 해결하는 방식의 문제 풀이에 적합함
• 앞서 언급된 팩토리얼 외에도 피보나치 수열, 하노이 탑 문제 풀이에 사용하기에 적합
• 이진 트리와 이진 탐색에 사용 되는 점이 가장 핵심

Iteration과의 비교

• 같은 업무를 반복하여 실시한다는 점에서 Iteration과 비교될 수 있음

Iteration

• for, while을 통해 구현
• 반복 조건이 for, while문에 명시됨
• 반복문 내부는 반복 시 실시할 시퀀스가 명시됨
• 자료 구조에 따라 재귀 방식보다 비효율적일 경우가 있음

• Tree나 Graph에서 동일한 일이 점차 작은 업무로 분산되는 특성을 가지는 경우 재귀 방식을 사용하는 것이 Iteration 방식을 활용하는 것보다 자연스러움
• 그러나 재귀 방식은 function call(함수 호출)을 반드시 포함하기 때문에 일반적으로 Iteration 방식보다는 느림
• 두 방식은 서로 전환 될 수 있음
  (재귀 방식으로 구현된 기능이 Iteration 방식으로도 구현될 수 있음)

팩토리얼 연산

• 둘다 시간복잡도는 O(n)으로 동일
• 재귀 방식은 추가적인 메모리 공간과 함수 호출을 위한 추가 비용이 발생해 실행 시간과 메모리 사용 측면에서 불리

x^n 연산

• Iteration 방식은 반복적으로 주어진 숫자 x를 n번 곱하므로 직관적이며 O(n)의 시간복잡도를 가짐
• Recursive 방식은
  종료 조건: n == 0일 때 1을 반환
  재귀 영역:
  n이 짝수일 때는 pow(x*x, n/2)를 호출
  n이 홀수일 때는 x * pow(x*x, (n-1)/2)를 호출
  

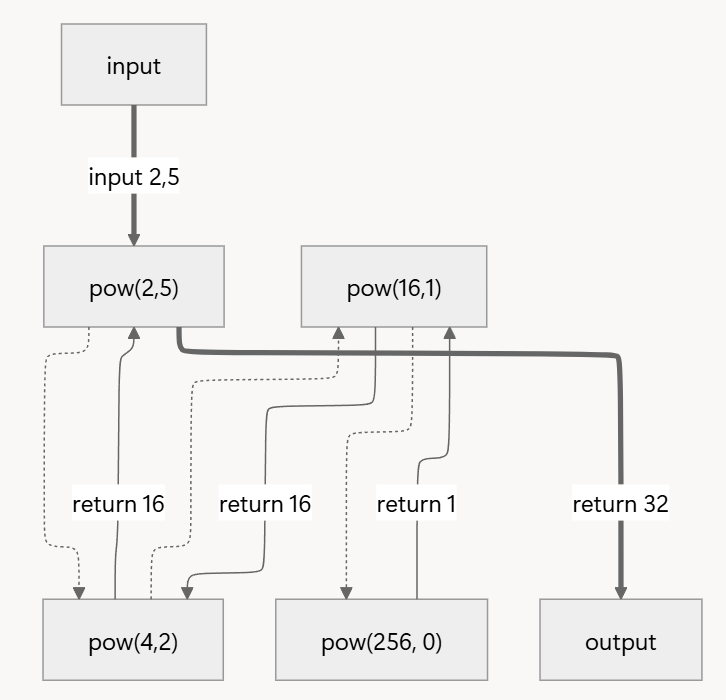
1. pow(2,5)에서 5 == 0이 false이고 5가 홀수이므로
   2 * pow(2 * 2, (5 -1)/2) 연산 과정에서 pow(4,2)를 호출
2. pow(4,2)에서 2 == 0이 false이고 4가 짝수이므로
   pow(4 * 4, 2 / 2) 연산 과정에서 pow(16,1)을 호출
3. pow(16,1)에서 1 == 0이 false이고 1이 홀수이므로
   16 * pow(16 * 16, (1 - 1) / 2 ) 연산 과정에서 pow(256, 0)을 호출
4. pow(256,0)은 종료 조건을 만족하므로 1을 반환
5. pow(16,1)은 16 * pow(256, 0)의 결과로 16을 반환
6. pow(4,2)는 pow(16,1)의 결과로 16을 반환
7. pow(2,5)는 2 * pow(4,2)의 결과인 32로 최종값을 도출

• 재귀 방식에서 함수 호출은 3번 발생
• 이와 같은 방식으로 x^n연산에서 재귀 방식은 O(log₂ n)의 복잡도를 가짐

피보나치 수열

• 피보나치 수열은 재귀 방식을 사용할 때 보다 간단하게 구현할 수 있는 연산 그러나 재귀 방식을 사용하면 비효율적임
• Recursive 방식으로 피보나치 수열 계산
  종료 조건:
  1) (n == 0) return 0
  2) (n == 1) return 1

재귀 호출:
fib(n - 1) + fib(n - 2)

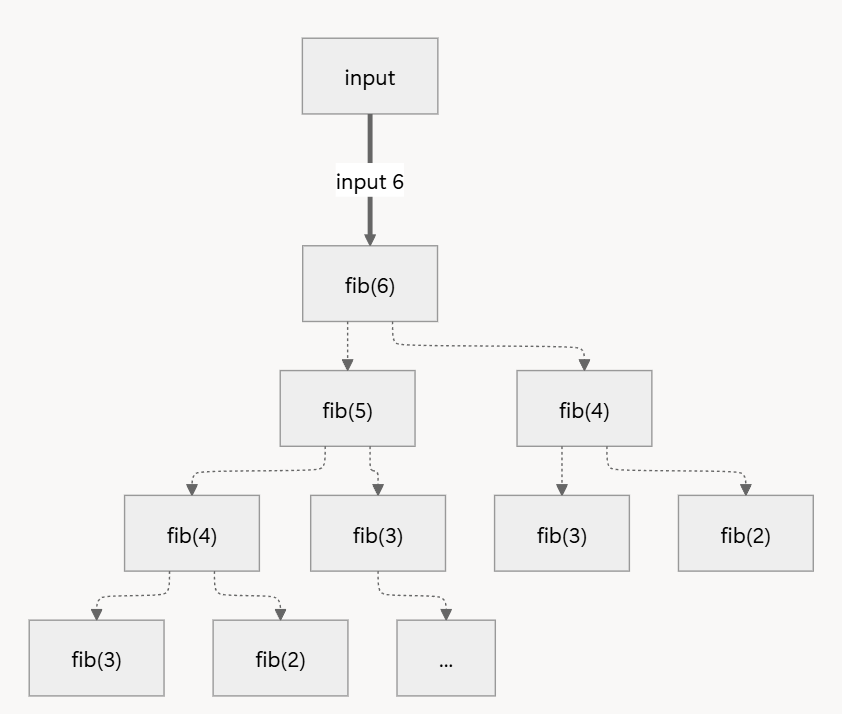
• fib(6)을 연산하는 과정에서 fib(4)나 fib(3)이 반복적으로 등장하며 동일한 연산을 독립적인 작업 내에서 따로 따로 실시하는 비효율적인 방식으로 동작

• Iteration 방식은 O(n)의 시간복잡도를 가지지만 재귀 방식은 O(2^n)의 복잡도를 가져 보다 비효율적임