8. 다이내믹 프로그래밍

기본적인 내용 정리글

---

✓ 다이내믹 프로그래밍 문제 접근 방법

1. 문제가 다이내믹 프로그래밍 유형인지 파악하기
   • 그리디, 완전 탐색 등 다른 알고리즘으로 풀이법 안 떠오를 때 적용
   • 완전 탐색 알고리즘 적용 시 시간이 오래 걸리면 부분 문제 중복 여부를 확인
2. 우선 단순한 재귀 함수로 비효율적인 프로그램 작성하기(탑다운)
   -> 작은 문제의 답으로 큰 문제 해결 가능함 확인
   -> 탑다운(Memoization)을 적용하여 코드 개선
3. 가능하다면 보텀엄(Tabulation) 방식을 우선시한다.
   (탑다운 방식은 재귀함수 호출로 인한 스택 오버플로우 오류 가능성이 있기 때문)
   (+) 다이내믹 프로그래밍 문제는 코딩테스트에서 주로 기본적인 수준으로 출제된다. 문제를 반복해서 푸는게 중요하다.
   
   

✓ 문제 풀이

1️⃣ 1로 만들기

2️⃣ 개미 전사

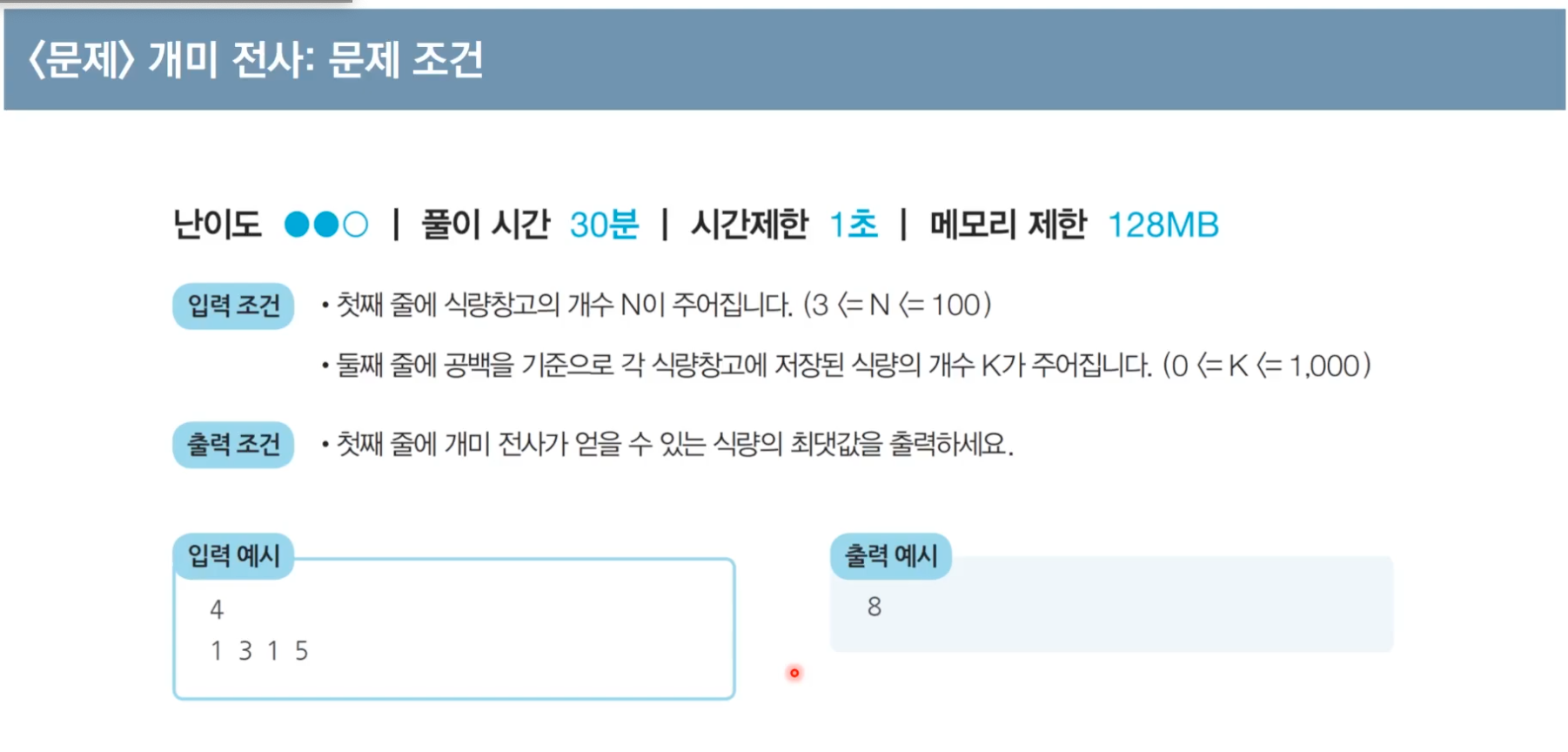
✓ 문제 해결 아이디어

• 최적구분구조: 왼쪽부터 차례대로 식량장고를 턴다고 했을 때, 특정한 i번쨰 식량창고에 대해 털지 안 털지 결정하려면, 두 가지 경우를 비교해서 더 큰 수를 선택하면 된다.
  + 1) (i-1)까지 턴 경우 # 현재 식량창고와 1칸 차이이므로, 현재 칸을 털 수 없음
  • 2) (i-2)까지 턴 경우+현재 식량창고
• 부분중복: (i-3)의 값은 (i-2) 경우에 중복되어 있으므로 따로 고려할 필요없음

✓ 정답 코드

# 정수 N을 입력 받기
n = int(input())
# 모든 식량 정보 입력 받기
array = map(int(input().split()))

# 앞서 계산된 결과를 저장하기 위한 DP테이블 초기화
d = [0] * 100     # 식량 창고 개수가 100개 이하임을 고려

# 다이나믹 프로그래밍으로 구현(보텀업)
d[0] = array[0]
d[1] = max(d[0], array[1])
for i in range(2,n):
	d[i] = max(d[i-1], d[i-2]+arrray[i])
    
# 계산된 결과 출력
print(d[n-1])

3️⃣ 바닥 공사

4️⃣ 효율적인 화폐 구성