[Java] 백준 1904 01타일

https://www.acmicpc.net/problem/1904

문제

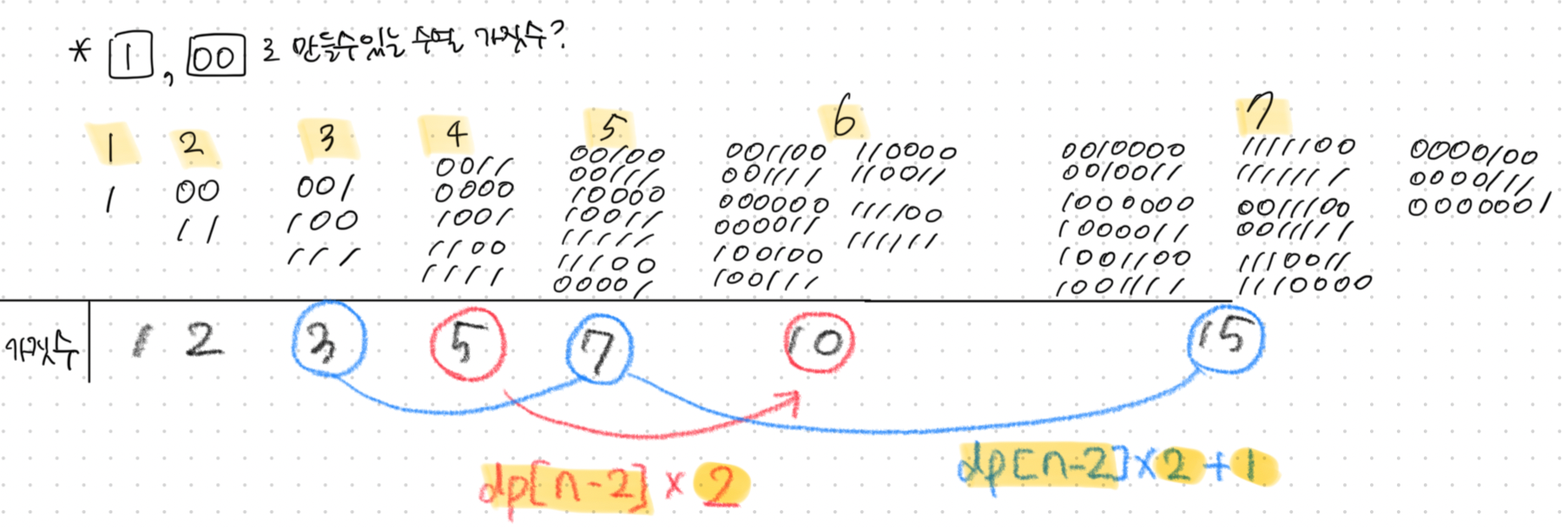
00, 1 만 사용해 N이 주어졌을때, 만들 수 있는 모든 가짓수?
예를 들어,
N=1) 1
N=2) 00, 11
N=4) 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열 만들 수 있음.

입력

첫째 줄에 N( 1<=N<1,000,000)

출력

첫째 줄에 N인 모든 2진 수열의 개수를 15746로 나눈 나머지 출력

예제 입력 1

4

예제 출력 1

5

풀이

dp 문제를 풀기위해, dp 테이블을 고려해보았다.

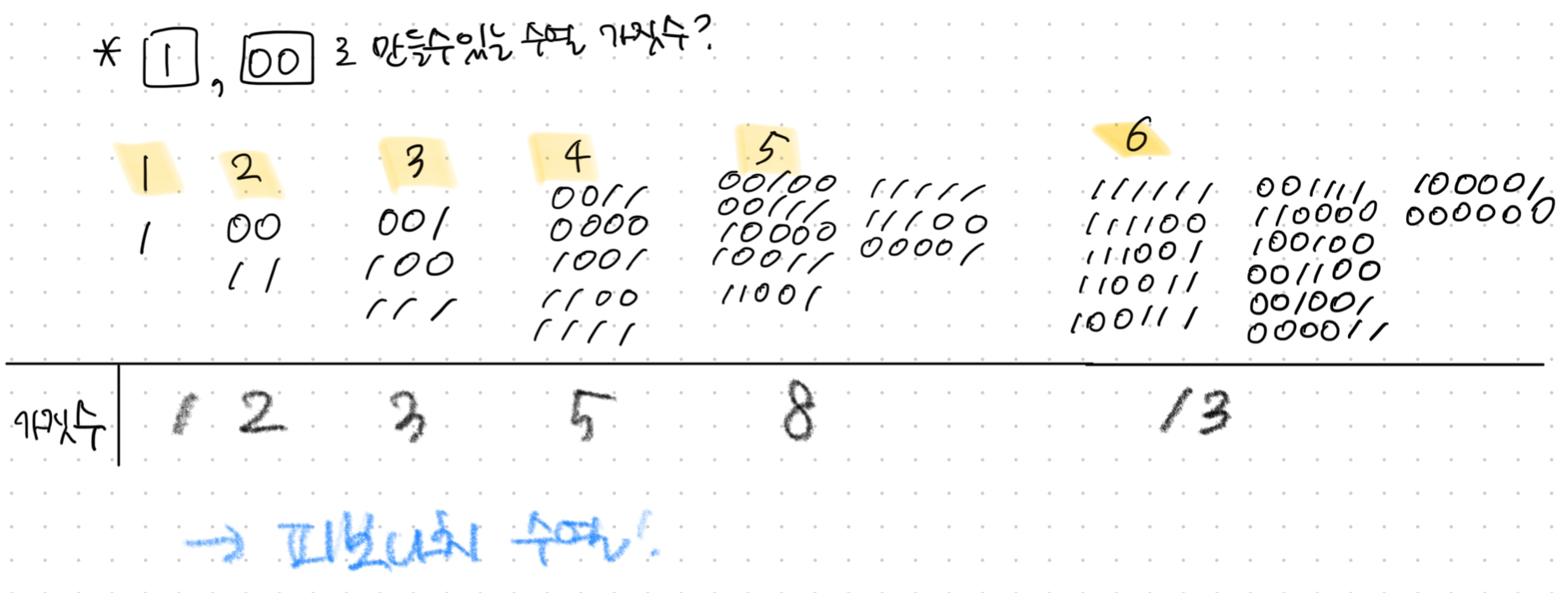
값을 나열해본 결과, 피보나치 수열의 패턴을 가짐을 확인할 수 있다.

dp[n]=dp[n-1]+dp[n-2]라는 점화식을 도출했으니, 코드로 구현해보자.

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        // 1. dp 테이블
        int[] dp = new int[1000001]; // 배열 사이즈 최댓값

        // 2. 초기값
        dp[1] = 1;
        dp[2] = 2;

        // 3. 점화식
        for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 2] + dp[i - 1]) % 15746;
        }
        System.out.println(dp[n]);
    }
}

배열 사이즈를 1000001로 초기화함에 주의하자.(n의 최댓값)