67. 정규화(Normalization)

정규화의 개요

• 정규화란 함수적 종속성 등의 종속성 이론을 이용하여 잘못 설계된 관계형 스키마를 더 작은 속성의 세트로 쪼개어 바람직한 스키마로 만들어 가는 과정이다.
• 하나의 종속성이 하나의 릴레이션에 표현될 수 있도록 분해해가는 과정이라 할 수 있다.
• 정규형에는 제1정규형, 제2정규형, 제3정규형, BCNF형, 제4정규형, 제5정규형이 있으며, 차수가 높아질수록 만족시켜야 할 제약 조건이 늘어난다.
• 정규화는 데이터베이스의 논리적 설계 단계에서 수행한다.
• 정규화는 논리적 처리 및 품질에 큰 영향을 미친다.
• 정규화된 데이터 모델은 일관성, 정확성, 단순성, 비중복성, 안정성 등을 보장한다.
• 정규화 수준이 높을수록 유연한 데이터 구축이 가능하고 데이터의 정확성이 높아지 는 반면 물리적 접근이 복잡하고 너무 많은 조인으로 인해 조회 성능이 저하된다.

정규화의 목적

• 데이터 구조의 안정성 및 무결성을 유지한다.
• 어떠한 릴레이션이라도 데이터베이스 내에서 표현 가능하게 만든다.
• 효과적인 검색 알고리즘을 생성할 수 있다.
• 데이터 중복을 배제하여 이상(Anomaly)의 발생 방지 및 자료 저장 공간의 최소화가 가능하다.
• 데이터 삽입 시 릴레이션을 재구성할 필요성을 줄인다.
• 데이터 모형의 단순화가 가능하다.
• 속성의 배열 상태 검증이 가능하다.
• 개체와 속성의 누락 여부 확인이 가능하다.
• 자료 검색과 추출의 효율성을 추구한다.

이상(Anomaly)의 개념 및 종류

• 정규화를 거치지 않으면 데이터베이스 내에 데이터들이 불필요하게 중복되어 릴레이션 조작 시 예기치 못한 곤란한 현상이 발생하는데, 이를 이상(Anomaly)이라 하며 삽입 이상, 삭제 이상, 갱신 이상이 있다.
• 삽입 이상(Insertion Anomaly): 릴레이션에 데이터를 삽입할 때 의도와는 상관없이 원하지 않은 값들도 함께 삽입되는 현상이다.
• 삭제 이상(Deletion Anomaly): 릴레이션에서 한 튜플을 삭제할 때 의도와는 상관없는 값들도 함께 삭제되는 연쇄가 일어나는 현상이다.
• 갱신 이상(Update Anomaly): 릴레이션에서 튜플에 있는 속성값을 갱신할 때 일부 튜플의 정보만 갱신되어 정보에 모순이 생기는 현상이다.

정규화의 원칙

• 정보의 무손실 표현, 즉 하나의 스키마를 다른 스키마로 변환할 때 정보의 손실이 있어서는 안 된다.
• 분리의 원칙, 즉 하나의 독립된 관계성은 하나의 독립된 릴레이션으로 분리시켜 표현해야 한다.
• 데이터의 중복성이 감소되어야 한다.

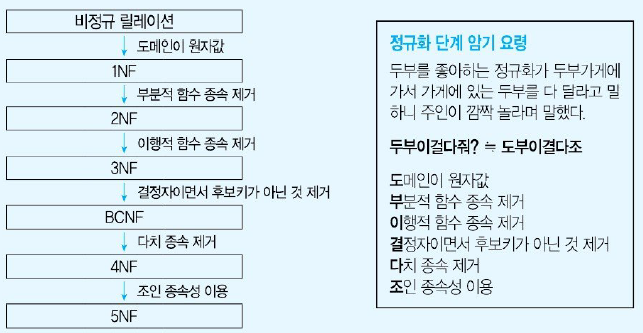
정규화 과정

1NF(제1정규형)

• 1NF는 릴레이션에 속한 모든 도메인(Domain)이 원자값(Atomic Value)만으로 되어 있는 정규형이다. 즉, 릴레이션의 모든 속성 값이 원자 값으로만 되어 있는 정규형이다.
• 릴레이션의 모든 속성이 단순 영역에서 정의된다.

2NF(제2정규형)

• 2NF는 릴레이션 R이 1NF이고, 기본키가 아닌 모든 속성이 기본키에 대하여 완전 함수적 종속을 만족하는 정규형이다.

함수적 종속/ 완전/부분 함수적 종속 및 이해

• 함수적 종속(Functional Dependency)

  • 함수적 종속은 데이터들이 어떤 기준값에 의해 종속되는 것을 의미합니다.
  • 예를 들어 <수강> 릴레이션이 (학번, 이름, 과목명)으로 되어 있을 때, '학번'이 결정되면 '과목명'에 상관없이 '학번'에는 항상 같은 '이름'이 대응됩니다. '학번'에 따라 '이름'이 결정될 때 '이름'을 '학번'에 함수 종속적이라고 하며 '학번' → '이름'과 같이 씁니다.

• 완전 함수적 종속

  • 어떤 테이블에서 속성 A가 다른 속성 집합 B 전체에 대해 함수적 종속이지만 속성 집합 B의 어떠한 진부분 집합이즉 CCB)에는 함수적 종속이 아닐 때 속성 A는 속성 집합 Bol 완전 함수적 종속이라고 합니다.

• 부분 함수적 종속

  • 어떤 테이블에서 속성 A가 다른 속성 집합 B 전체에 대해 함수적 종속이면서 속성 집합 B의 어떠한 진부분 집합에도 함수적 종속일 때 속성 A는 속성 집합 B에 부분 함수적 종속이라고 합니다.

• 완전/부분 함수적 종속의 이해

  • 완전 함수적 종속은 어떤 속성이 기본키에 대해 완전히 종속적일 때를 말합니다.
  • 예를 들어 <수강> 릴레이션이 (학번, 과목명, 성적, 학년)으로 되어 있고 (학번, 과목명)이 기본키일 때, '성적'은 '학번'과 '과목명'이 같을 경우에는 항상 같은 '성적'이 옵니다. 즉 '성적'은 '학번'과 '과목명'에 의해서만 결정되므로 '성적'은 기본키(학번, 과목명)에 완전 함수적 종속이 되는 것입니다.
  • 반면에 '학년'은 '과목명'에 관계없이 '학번'이 같으면 항상 같은 '학년'이 옵니다. 즉 기본키의 일부인 '학번'에 의해서 '학년'이 결정되므로 '학년'은 부분 함수적 종속이라고 합니다.

3NF(제3정규형)

• 3NF는 릴레이션 R이 2NF이고, 기본키가 아닌 모든 속성이 기본키에 대해 이행적 종속을 만족하지 않는 정규형이다.
• 무손실 조인 또는 종속성 보존을 저해하지 않고도 항상 3NF 설계를 얻을 수 있다.

BCNF(Boyce-Codd 정규형)

• BCNF는 릴레이션 R에서 결정자가 모두 후보키(Candidate Key)인 정규형이다.
• 3NF에서 후보키가 여러 개 존재하고 서로 중첩되는 경우에 적용하는 강한 제3정규형이라고도 한다.
• 모든 BCNF(Boyce-Codd Normal Form)가 종속성을 보존하는 것은 아니다.
• BCNF의 제약 조건
  • 키가 아닌 모든 속성은 각 키에 대하여 완전 종속해야 한다.
  • 키가 아닌 모든 속성은 그 자신이 부분적으로 들어가 있지 않은 모든 키에 대하여 완전 종속해야 한다.
  • 어떤 속성도 키가 아닌 속성에 대해서는 완전 종속할 수 없다.

4NF(제4정규형)

• 4NF는 릴레이션 R에 다치 종속 A ↠ B가 성립하는 경우 R의 모든 속성이 A에 함수적 종속관계를 만족하는 정규형이다.

5NF(제5정규형, PJ/NF)

• 5NF는 릴레이션 R의 모든 조인 종속이 R의 후보키를 통해서만 성립되는 정규형이다.

정규화 과정 정리