(Algorithm) Binary Search

Mirrer·2023년 1월 3일

algorithm

Algorithm

목록 보기

7/15

Sequential Search

리스트의 모든 데이터를 차례대로 탐색하여 원하는 데이터를 검색하는 Algorithm

순차 탐색(Sequential Search)은 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 모든 데이터를 하나씩 확인하는 방법이다.

보통 정렬되지 않은 리스트에서 데이터를 찾아야 할 때 사용하며, 리스트 내에 데이터가 아무리 많아도 시간만 충분하다면 항상 원하는 원소(데이터)를 찾을 수 있다는 장점이 있다.

데이터의 개수가 N 개일 때 순차 탐색은 최대 N 번의 비교 연산이 필요하므로 최악의 경우 시간 복잡도는 $O(N)$ 이다.

Example

순차 탐색을 구현하면 다음과 같다.

const target = 4;
const arr = [1, 2, 3, 5, 12, 4, 7, 9, 24, 26, 14, 35];

const sequentialSearch = (target, arr) => {
  for (let i =0; i < arr.length; i++) { // 배열 전체를 탐색
   if (arr[i] === target) return i // 원소의 값과 taget이 일치한다면 그 값을 반환
  }
  return -1;
};

console.log(sequentialSearch(target, arr));

// 실행 결과
5

Binary Search

검색 범위를 좁혀 나가면서 원하는 데이터를 검색하는 Algorithm

이진 탐색(Binary Search)은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.

이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정하며, 반복문, 재귀함수...등을 이용하여 구현할 수 있다,

구체적인 동작 과정은 다음과 같다.

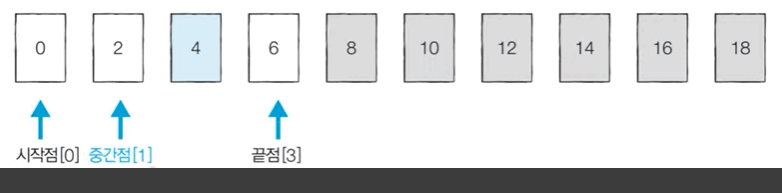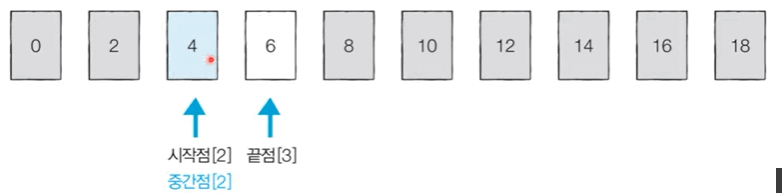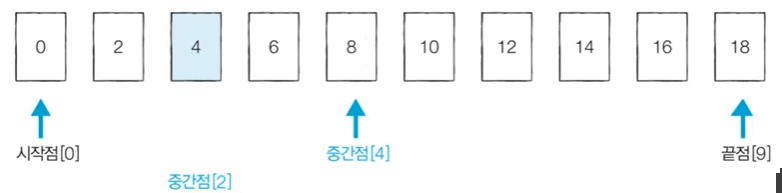
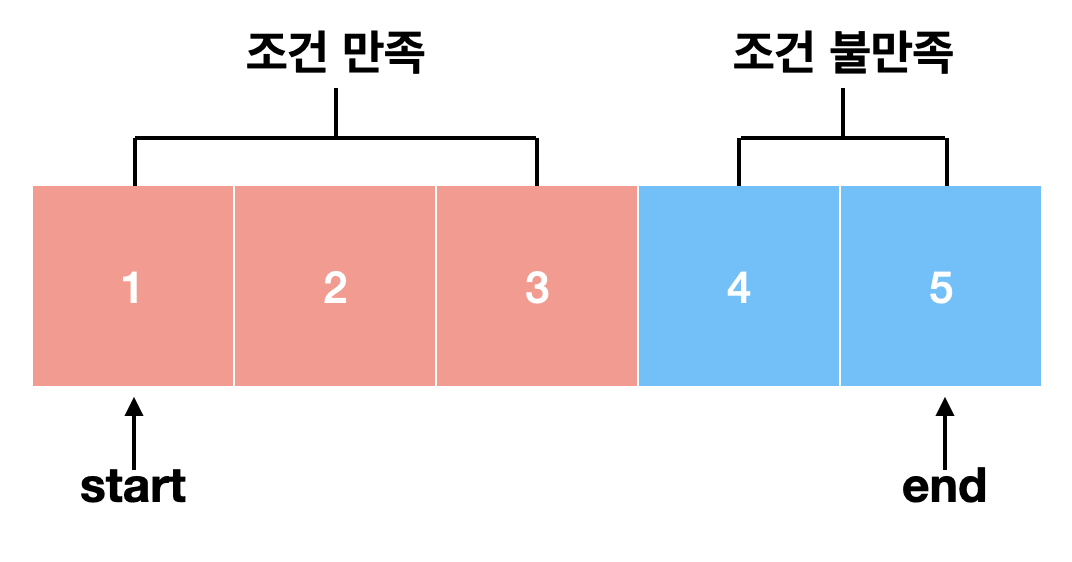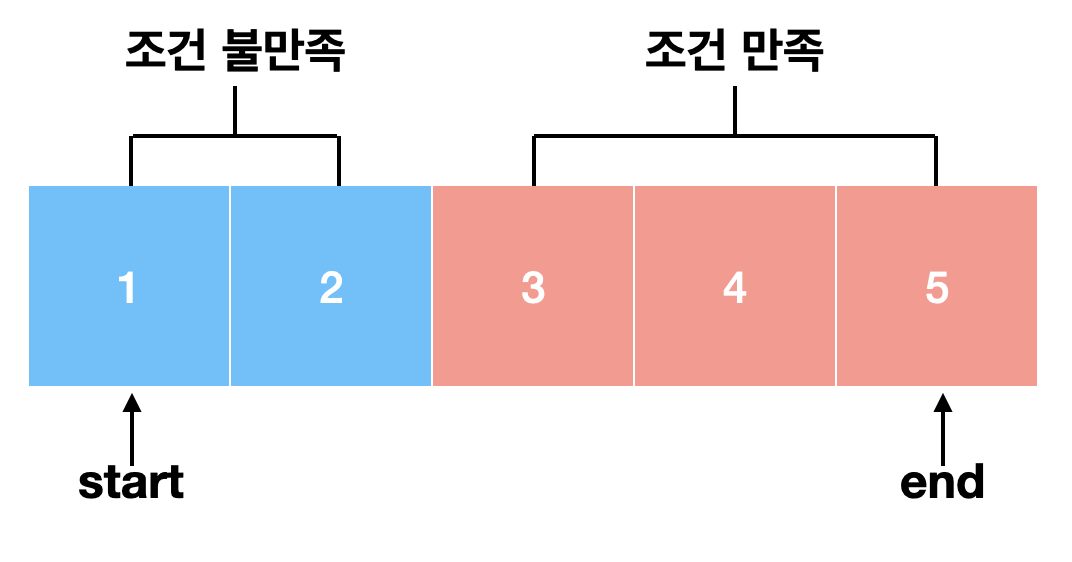
[Step 0]. 정렬된 데이터 중 값이 4인 원소를 찾기 위해 시작점: 0, 끝점: 9, 중간점: 4를 지정한다.
[Step 1]. 중간 값 '8'과 찾는 값인 '4'와 비교하여 중간 값이 더 크다면 중간점의 오른쪽에 위치한 값들은 확인할 필요가 없다.
[Step 2]. 시작점: 0, 끝점: 3, 중간점: 1를 지정한다.
[Step 3]. 중간 값 '2'보다 찾는 값 '4'가 더 크기 때문에 중간점을 포함한 왼쪽 데이터는 확인할 필요가 없다.
[Step 4]. 시작점:2, 끝점: 3, 중간점: 2를 지정한다.
[Step 5]. 찾는 값 '4'는 인덱스 2에 위치한다는 것을 확인할 수 있다.

위 예제의 전체 데이터의 개수는 10개이지만, 이진 탐색을 이용해 총 3번의 탐색으로 원소를 찾을 수 있다.

즉, 탐색 데이터를 절반씩 줄이는 점은 앞선 포스팅에서 소개한 퀵 정렬과 동일하다.

Example

이진 탐색을 구현하면 다음과 같다.

const [N, target] = [10, 3];
const arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]; // 4 

function binarySearch(arr, target, start, end) {
  while (start <= end) {
    const mid = Math.floor((start + end) / 2);

    if (arr[mid] === target) return mid; // 찾은 경우 중간점 인덱스 반환
    else if (arr[mid] > target) end = mid - 1;
    else start = mid + 1;
  }
  return -1;
};

const result = binarySearch(arr, target, 0, N - 1);
console.log(result === -1 ? '배열에 N이 존재하지 않습니다.' : result + 1);

// 실행 결과
2

Time Complexity

이진 탐색은 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 $log^2N$ 에 비례한다.

즉, 이진 탐색은 탐색 범위를 절반씩 줄이기 때문에 $O(logN)$ 의 시간 복잡도를 보장한다.

[Step 0]. 32개의 탐색 데이터가 주어진다.
[Step 1]. 이상적인 1단계를 거치면 16개 가량의 데이터가 남는다.
[Step 2]. 2단계를 거치면 8개 가량의 데이터가 남는다.
[Step 3]. 3단계를 거치면 4개 가량의 데이터가 남는다.

Parametric Search

파라메트릭 서치(Parametric Search)는 최적화 문제를 결정 문제('예' 혹은 '아니오')로 바꾸어 해결하는 기법이다.

최적화 문제는 문제의 상황을 만족하는 특정 변수의 최소값, 최대값을 구하는 문제
(ex) 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제

일반적으로 코딩 테스트에서 파라메트릭 서치 문제는 이진 탐색을 이용하여 해결할 수 있다.

Problem 1, 떡볶이 떡 만들기

동빈이네 떡볶이 떡은 재밌게도 떡볶이 떡의 길이가 일정하지 않습니다. 그래서 대신에 한 봉지 안에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰줍니다.

여기서 절단기에 높이(H)를 지정하면 줄지어진 떡을 한 번에 절단하며, 높이가 H보다 긴 떡은 H 위의 부분이 잘릴 것이고, 낮은 떡은 잘리지 않습니다.

예를 들어 높이가 19, 14, 10, 17cm인 떡이 나란히 있고 절단기 높이를 15cm로 지정하면 자른 뒤 떡의 높이는 15, 14, 10, 15cm가 될 것입니다.

잘린 떡의 길이는 차례대로 4, 0, 0, 2cm입니다. 손님은 6cm만큼의 길이를 가져갑니다.

손님이 왔을 때 요청한 총 길이가 M일 때 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하세요.

Explanation

위 문제는 전형적인 이진 탐색, 또는 파라메트릭 서치 유형의 문제이다.

구체적인 풀이과정은 다음과 같다.

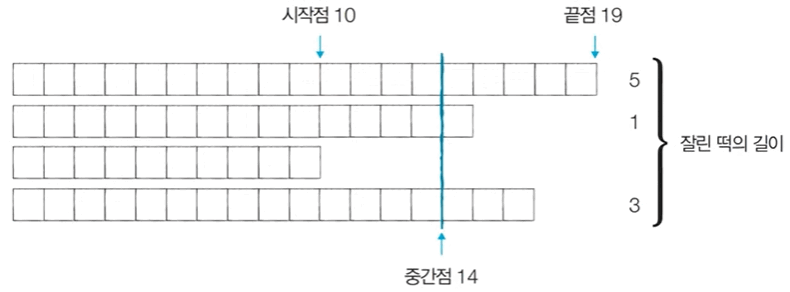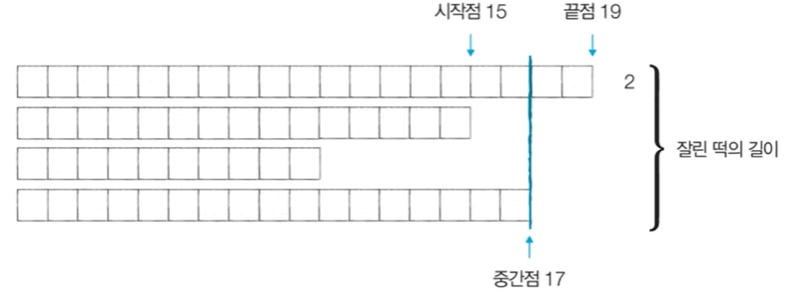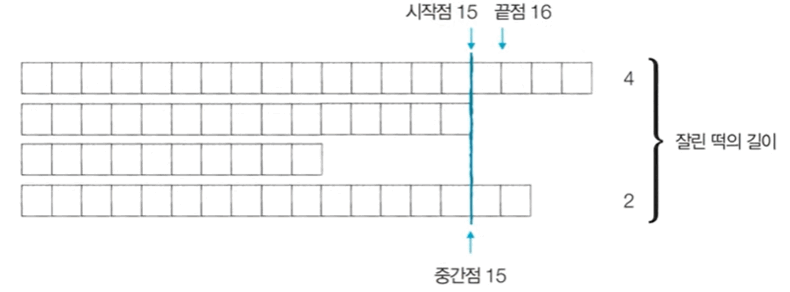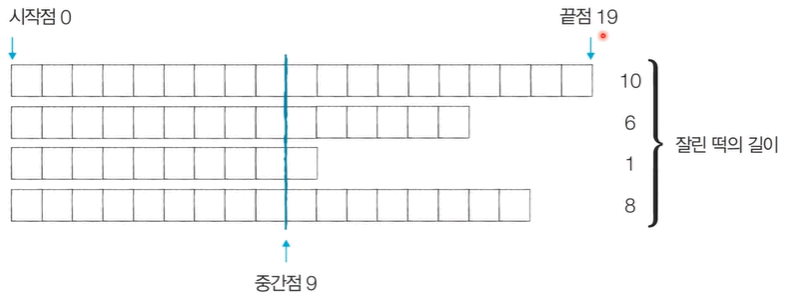
[Step 0]. 0, 19 사이의 중간점 9를 절단기 높이 H로 설정하여 얻을 수 있는 떡의 합( $10 + 6 + 1 + 8 = 25$ )을 구한다.
[Step 1]. 필요한 떡의 길이가 6보다 크기 때문에 시작점을 증가시킨다.
[Step 2]. 절단기 높이를 14로 설정하여 떡의 합 ( $5 + 1 + 3 = 9$ )을 구한다.
[Step 3]. 여전히 필요한 떡의 길이인 6보다 크기 때문에 시작점을 증가시킨다.
[Step 4]. 필요한 떡의 길이인 6보다 작다면 끝점을 감소시킨다.

위 이진 탐색 과정을 반복하면 답을 도출할 수 있다.

중간점의 값은 시간이 지날수록 '최적화된 값'이 되기 때문에, 과정을 반복하면서 얻을 수 있는 떡의 길이 합이 필요한 떡의 길이보다 크거나 같을 때마다 중간점의 값을 기록한다.

위 과정을 코드로 구현하면 다음과 같다.

const [N, M] = [4, 6];
const arr = [19, 15, 10, 17];

// 이진 탐색을 위한 시작, 끝점 설정
let start = 0;
let end = Math.max(...arr);
let result = 0;

while (start <= end) {
  let total = 0;
  let mid = Math.floor((start + end) / 2);

  for (let i = 0; i < N; i++) { // 자른 떡의 양 계산
    if (arr[i] > mid) total += arr[i] - mid;
  }

  if (total < M) { // 떡의 양이 부족한 경우 더 많이 자르기(왼쪽 부분 탐색)
    end = mid - 1;
  } else { // 떡의 양이 충분한 경우 덜 자르기(오른쪽 부분 탐색)
    result = mid; // 최대한 덜 잘랐을 때가 정답이므로, result에 기록
    start = mid + 1;
  }  
}

console.log(result);

// 실행 결과
15

Problem 2, 정렬된 배열에서 특정 수의 개수 구하기

N개의 원소를 포함하고 있는 수열이 오름차순으로 정렬되어 있을 때, 수열에서 x가 등장하는 횟수를 계산하시오.

예를 들어 수열 ${1, 1, 2, 2, 2, 2, 3}$ 이 있을 때 $x = 2$ 라면, 현재 수열에서 값이 2인 원소가 4개이므로 4를 출력한다.

단, 이 문제는 시간 복잡도 $O(logN)$ 으로 알고리즘을 설계하지 않으면 시간 초과 판정을 받는다.

Explanation

위 문제는 데이터가 정렬되어 있다는 조건과 함께 시간 복잡도 $O(logN)$ 을 요구하고 있어 일반적인 선형 탐색을 구현한다면 시간 초과 판정을 받는다.

그래서 해당 문제는 이진 탐색을 통해 특정 값이 등장하는 첫 번째, 마지막 위치를 찾아 위치 차이를 계산하여 문제를 해결할 수 있다.

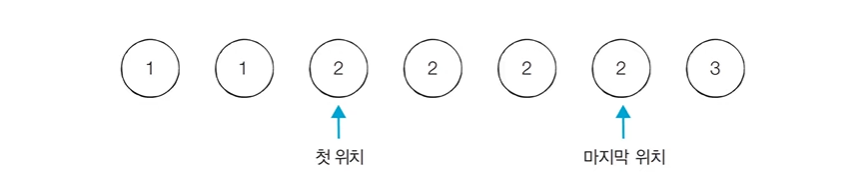
이진 탐색을 이용하여 문제를 해결한 코드는 다음과 같다.

const [N, X] = [7, 2];
const arr = [1, 1, 2, 2, 2, 2, 3];

function leftIndex(start, end) { // 첫 번째 위치 구하기
  while (start < end) {
    const mid = Math.floor((start + end) / 2);
    if (arr[mid] >= X) end = mid;
    else start = mid + 1;
  }
  return end;
}

function rightIndex(start, end) { // 마지막 위치 구하기
  while (start < end) {
    const mid = Math.floor((start + end) / 2);
    if (arr[mid] > X) end = mid;
    else start = mid + 1;
  }
  return end;
}

const left = leftIndex(0, N);
const right = rightIndex(0, N);
console.log(right - left === 0 ? -1 : right - left);