---

Sort Algorithm

n 개의 숫자 입력을 사용자가 지정한 기준에 맞게 정렬하여 출력하는 Algorithm

정렬(Sorting)이란 데이터를 특정한 기준에 따라 순서대로 나열하는 것을 의미한다.

일반적으로 문제 상황에 따라 적절한 정렬 알고리즘을 선택하여 공식처럼 사용한다.

위 숫자 카드를 오름차순으로 정렬할 때 컴퓨터는 인간과 다르게 데이터의 규칙성을 직관적으로 알 수 없다.

그래서 어떻게 정렬을 수행할지에 대한 과정을 소스코드로 작성하여 구체적으로 명시해야 한다.

---

Selection Sort

선택 정렬(Selection Sort)은 처리되지 않은 데이터 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복한다.

구체적인 동작 과정은 다음과 같다.

[Step 0]. 처리되지 않은 데이터 중 가장 작은 '0' 을 선택해 가장 앞의 '7' 과 바꾼다.
[Step 1]. 처리되지 않은 데이터 중 가장 작은 '1' 을 선택해 가장 앞의 '5' 와 바꾼다.
[Step 2]. 처리되지 않은 데이터 중 가장 작은 '2' 를 선택해 가장 앞의 '9' 와 바꾼다.
[Step 3]. 위 과정을 반복하여 가장 작은 것을 선택해 앞으로 보내 전체 데이터를 정렬한다.

Example

선택 정렬을 코드로 구현하면 다음과 같다.

const arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8];

for (let i = 0; i < arr.length; i++) {
  let min_index = i; // 가장 작은 원소의 인덱스
  
  for (let j = i + 1; j < arr.length; j++) {
    if (arr[min_index] > arr[j]) {
      const temp = arr[min_index]; // swap
      arr[min_index] = arr[j];
      arr[j] = temp;
    }
  }
}

console.log(arr.join(' '));

// 실행 결과 
0 1 2 3 4 5 6 7 8 9

Time Complexity

선택 정렬은 N 번 만큼 가장 작은 수를 찾아서 맨 앞으로 보낸다.

구현 방식에 따라서 사소한 오차는 있을 수 있지만 전체 연산 횟수는 아래와 같다.

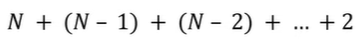
위 식은 $(N^2 + N + 2) / 2$로 표현할 수 있으며, Big-O Notation에 따라 $O(N^2)$이라고 작성한다.

---

Insertion Sort

삽입 정렬(Insertion Sort)은 처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입한다.

선택 정렬에 비해 구현 난이도가 높은 편이지만, 일반적으로 더 효율적으로 동작한다.

구체적인 동작 과정은 다음과 같다.

[Step 0]. 첫 번째 데이터 '7' 은 그 자체로 정렬이 되어 있다고 판단하고, 두 번째 데이터인 '5' 가 어떤 위치로 들어갈지 판단한다.
[Step 1]. '7' 의 왼쪽으로 들어가거나 오른쪽으로 들어가거나 두 경우만 존재한다.
[Step 2]. 이어서 '9' 가 어떤 위치로 들어갈지 판단한다.
[Step 3]. '9' 는 차례대로 왼쪽에 있는 데이터와 비교해서 왼쪽 데이터보다 더 작다면 위치를 바꿔 주고 그렇지 않다면 그냥 그자리에 머물러 있도록 한다.
[Step 4]. '0' 은 '9' ,'7' ,'5' 와 비교했을 때 모두 작기 때문에 '5'의 왼쪽에 위치한다.
[Step 5]. 위 과정을 반복하여 정렬이 완성된다.

Example

삽입 정렬을 코드로 구현하면 다음과 같다.

const arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8];

for (let i = 1; i < arr.length; i++) {
  for (let j = i; j > 0; j--) { // 인덱스 i부터 1까지 1씩 감소하며 반복
    if (arr[j] < arr[j - 1]) { // 한 칸씩 왼쪽으로 이동
      const temp = arr[j];
      arr[j] = arr[j - 1];
      arr[j - 1] = temp;
    } else break; // 작은 데이터를 만나면 그 위치에서 정지
  }
}

console.log(arr.join(' '));

// 실행 결과 
0 1 2 3 4 5 6 7 8 9

Time Complexity

삽입 정렬의 시간 복잡도는 $O(N^2)$이며, 선택 정렬과 마찬가지로 반복문이 두 번 중첩되어 사용된다.

삽입 정렬은 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작한다.

최선의 경우 $O(N)$의 시간 복잡도를 가진다.

---

Quick Sort

퀵 정렬(Quick Sort)은 기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법이다.

일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나이며, 병합 정렬과 더불어 대부분의 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘이다.

가장 기본적인 퀵 정렬은 첫 번째 데이터를 기준 데이터(pivot)로 설정한다.

구체적인 동작 과정은 다음과 같다.

[Step 0]. 피벗의 값은 '5' 이며, 왼쪽은 '5' 보다 큰 '7' , 오른쪽은 '5' 보다 작은 '4' 가 선택된다.
[Step 1]. 왼쪽은 '5' 보다 큰 '9' , 오른쪽은 '5' 보다 작은 '2' 을 선택하여 두 데이터의 위치를 서로 변경한다.
[Step 2]. 왼쪽은 '5' 보다 큰 '6' , 오른쪽은 '5' 보다 작은 '1' 을 선택한다.
[Step 3]. 두 데이터의 위치가 엇갈려 'pivot'과 작은 데이터 위치를 서로 변경한다.
[Step 4]. 위 과정을 마쳐 '5' 의 왼쪽은 '5' 보다 작고, 오른쪽은 '5' 보다 크다는 특징이 있다. 이러한 과정을 피벗 기준 데이터 분할(Divide)이라고 한다.
[Step 5]. 분할된 왼쪽, 오른쪽 데이터에 위 과정을 반복하여 전체 데이터를 정렬한다.

퀵 정렬은 이상적 분할이 일어났을 경우 전체 연산 횟수로 $O(NlogN)$이 되어 빠른 정렬을 기대할 수 있다.

너비 X 높이 = $N X logN$ = $NlogN$

Example

퀵 정렬을 코드로 구현하면 다음과 같다.

const arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8];

//  배열의 왼쪽 인덱스, 오른쪽 인덱스 기본값 설정
function quickSort(array, left = 0, right = array.length - 1) {
  if (left >= right) return;

  function divide(array, left, right, pivot) {
    while (left <= right) {
      while (array[left] < pivot) left++;
      while (array[right] > pivot) right--;

      if (left <= right) {
        let swap = array[left];
        array[left] = array[right];
        arr[right] = swap;
        left++;
        right--;
      }
    }
    return left;
  }

  const mid = Math.floor((left + right) / 2);
  const pivot = array[mid]; // 중간 pivot
  const partition = divide(array, left, right, pivot); // 왼쪽과 오른쪽 인덱스를 이동하며 값을 교환

  // partition 인덱스를 기준으로 배열을 왼쪽 배열, 오른쪽 배열로 나눠서 다시 재귀 호출
  quickSort(array, left, partition - 1);
  quickSort(array, partition, right);

  return array;
}

console.log(quickSort(arr));

// 실행 결과
0 1 2 3 4 5 6 7 8 9

Time Complexity

퀵 정렬은 첫 번째 원소를 피벗으로 지정하여, 이미 정렬된 배열에 대해 퀵 정렬을 수행하는 경우 최악의 효율로 동작한다.

일반적으로 평균 $O(NlogN)$의 시간 복잡도를 가지지만, 최악의 경우 $O(N^2)$의 시간 복잡도를 가진다.

---

Counting Sort

계수 정렬(Counting Sort)은 사용 조건이 제한되있지만, 사용시 매우 빠른 속도를 보장하는 정렬 알고리즘이다.

계수 정렬은 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능하다.

데이터의 개수가 N , 데이터(양수) 중 최댓값이 K 일 때 최악의 경우에도 수행시간 $O(N+K)$를 보장한다.

구체적인 동작 과정은 다음과 같다.

[Step 0]. 가장 작은 데이터부터 가장 큰 데이터까지의 범위가 모두 담길 수 있도록 리스트를 생성한다.
[Step 1]. 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가시킨다.
[Step 2]. 최종 리스트에는 각 데이터가 몇 번씩 등장했는지 그 횟수가 기록된다.
[Step 3]. 각각의 데이터 횟수를 참고하여 요소 갯수를 정렬한다.

Example

계수 정렬을 코드로 구현하면 다음과 같다.

const arr = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2];
const count = Array(10).fill(0);
let sorted = [];

for (let i = 0; i < arr.length; i++) {
  count[arr[i]]++; // 각 데이터에 해당하는 인덱스의 값 증가
};

for (let i = 0; i < count.length; i++) { // 리스트에 기록된 정렬 정보 확인
  const sortedNum = Array(count[i]).fill(i); // 반복된 횟수만큼 요소를 배열에 추가
  sorted = sorted.concat(sortedNum);
}

console.log(sorted.join(' '));

// 실행 결과
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9

Time Complexity

계수 정렬의 시간 복잡도와 공간 복잡도는 모두 $O(N+K)$이다.

계수 정렬은 때에 따라서 심각한 비효율성을 초래할 수 있다.

데이터가 '0' 과 '999,999' 로 단 2개만 존재하는 경우, 백만개 만큼의 원소가 담길 수 있는 배열을 만들어야 한다.

그래서 계수 정렬은 동일한 값을 가지는 데이터가 여러 개 등장할 때 효과적으로 사용할 수 있다.

---

참고 자료

(이코테 2021) 이것이 취업을 위한 코딩 테스트다 - 동빈나