Disjoint Sets

공통 원소가 없는 두 집합

서로소 집합(Disjoint Sets)은 두 집합 사이에 공통 원소가 존재하지 않는 경우를 의미하며, 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리한다.

또한 서로소 집합 자료구조는 아래와 같은 연산을 수행한다.

• 초기화: n개의 원소가 각각의 집합에 포함되어 있도록 초기화
• 합집합(Union): 두 원소 a, b가 주어질 때 이들이 속한 두 집합을 하나로 병합
• 찾기(Find): 어떤 원소 a가 주어질 때 이 원소가 속한 집합을 반환

Action Process

서로소 집합 자료구조는 합치기 찾기(Union Find) 자료구조라고도 불리며, 여러 개의 합치기 연산이 주어졌을 때 서로소 집합 자료구조의 동작 과정은 다음과 같다.

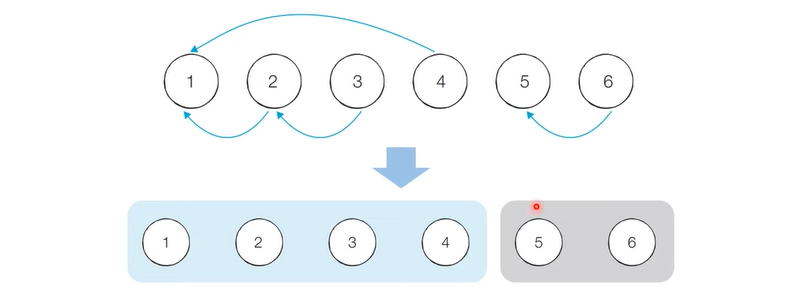
[Step 1]. 합집합 연산을 확인하여, 서로 연결된 두 노드 $A$, $B$를 확인
[Step 2]. $A$, $B$의 루트 노드 $A'$, $B'$를 각각 찾는다.
[Step 3]. $A'$, $B'$의 부모 노드로 설정한다.
[Step 4]. 모든 합집합 연산을 처리할 때까지 1번의 과정을 반복한다.

서로소 집합 자료구조에서는 연결성을 통해 손쉽게 집합의 형태를 확인할 수 있다.

기본적인 형태의 서로소 집합 자료구조에서는 루트 노드에 즉시 접근할 수 없으며, 루트 노드를 찾기 위해 부모 테이블을 계속해서 확인하여 거슬로 올라가야 한다.

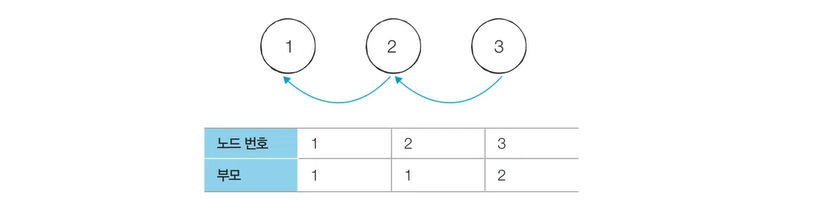
위 과정을 코드로 구현하면 다음과 같다.

class NaiveDisjointSet {    
    constructor(n) {
        this.parent = new Array(n).fill(0).map((_, i) => i);
    }
    
    find(u) {
        if (u === this.parent[u]) return u;
        return this.find(this.parent[u]);
    }
    
    merge(u, v) {
        let u_root = this.find(u);
        let v_root = this.find(v);
        
        if (u_root === v_root) return;
        
        this.parent[u] = v;
    }
}

Optimization

위 코드와 같이 트리를 사용하여 서로소 집합을 구현하면 연산의 순서에 따라 트리가 한쪽에 치우쳐질 수 있다는 문제를 피할 수 없다.

그래서 위와 같은 문제를 해결하기 위해 트리를 합칠 때 항상 '높이가 더 낮은 트리'를 '높이가 더 높은 트리' 밑으로 이동시켜 트리가 치우쳐지는 상황을 방지한다.

이러한 최적화 방법을 랭크에 의한 합치기(union-by-rank) 최적화라고 한다.

class DisjointSet {    
    constructor(n) {
        this.parent = new Array(n).fill(0).map((_, i) => i);
        // 노드가 한 트리의 루트인 경우 해당 트리의 높이를 저장한다.
        this.rank = new Array(n).fill(1); 
    }
    
    find(u) {
        if (u === this.parent[u]) return u;
        // parent[u]를 루트로 바꿔 다음번에 find(u)가 호출됐을 때는 경로를 따라 찾아 올라갈 필요가 없어지게 한다.      
        return this.parent[u] = this.find(this.parent[u]);
    }
    
    merge(u, v) {
        let u_root = this.find(u);
        let v_root = this.find(v);
        
        if (u_root === v_root) return;

        if (this.rank[u_root] > this.rank[v_root]) [this.rank[u_root], this.rank[v_root]] = [this.rank[v_root], this.rank[u_root]];
        // 이제 rank[v_root]가 항상 rank[u_root] 이상이므로 u_root를 v_root의 자식으로 넣는다.
        this.parent[u_root] = v_root;

        if (this.rank[u_root] === this.rank[v_root]) this.rank[v_root]++;
    }
}

이렇게 최적화 된 서로소 집합은 찾기, 합치기 연산을 아주 많이 수행했을 때, 각 수행에 대해 상수 시간에 동작한다.

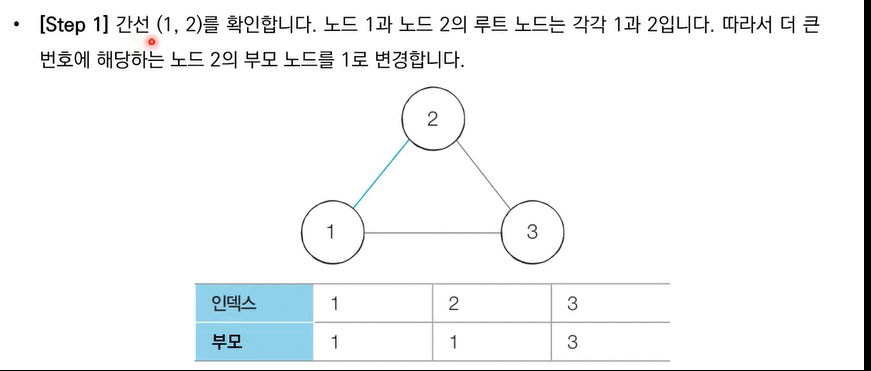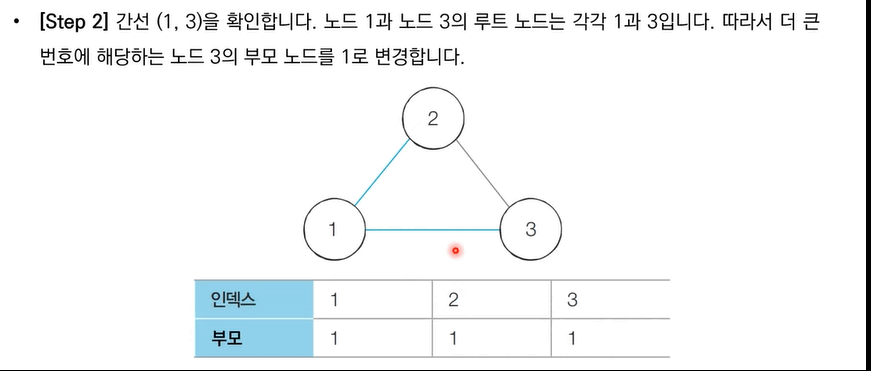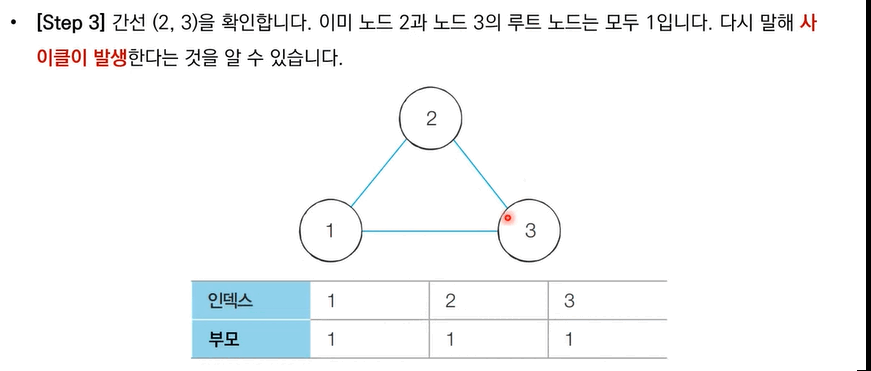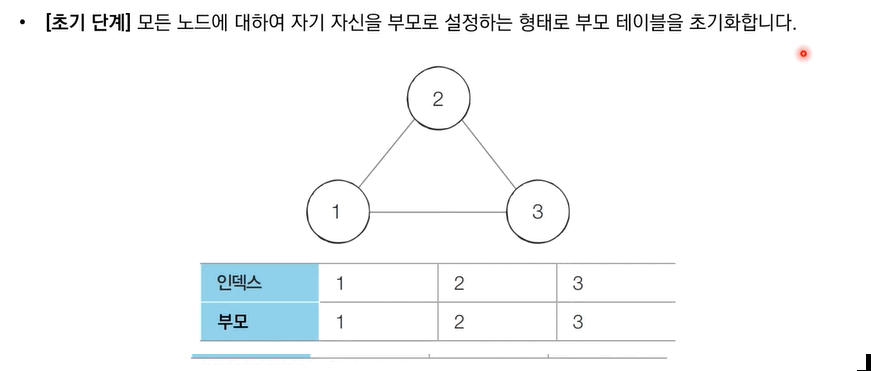
또한 서로소 집합은 아래와 같은 과정을 통해 무방향 그래프 내에서의 Cycle을 판별할 때 사용할 수 있다.

[Step 1]. 각 간선을 하나씩 확인하며 두 노드의 루트 노드를 확인
[Step 2]. 루트 노드가 서로 다르다면 두 노드에 대해 합집합 연산을 수행
[Step 3]. 루트 노드가 서로 같다면 사이클이 발생
[Step 4]. 그래프에 포함되어 있는 모든 간선에 대하여 위 과정을 반복한다.

참고 자료

(이코테 2021) 이것 취업을 위한 코딩 테스트다 - 동빈나