(Algorithm) Spanning Tree, Kruskal

Mirrer·2023년 1월 6일

algorithm

Algorithm

목록 보기

12/15

Spanning Tree

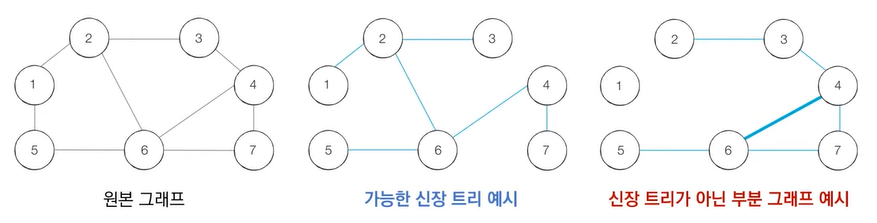
신장 또는 생성 부분 그래프는 그래프 이론에서 모든 꼭짓점을 포함하는 부분 그래프

신장 트리(Spanning Tree)는 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.

그래서 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 조건이기도 하다.

Minimum Spanning Tree

최소 신장 트리(Minimum Spanning Tree, MST)는 최소한의 비용으로 구성되는 신장 트리를 찾는다.

예를 들어 $N$ 개의 도시가 존재하는 상황에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있게 도로를 설치한다고 가정한다.

이 때 두 도시 $A$ , $B$ 를 선택했을 때 $A$ 에서 $B$ 로 이동하는 경로가 반드시 존재하도록 도로를 설치한다.

Kruskal

크루스칼(Kruskal) 알고리즘은 위에서 설명한 최소 신장 트리의 대표적인 알고리즘이다.

크루스칼은 그리디 알고리즘으로 분류되며, 구체적인 동작 과정은 다음과 같다.

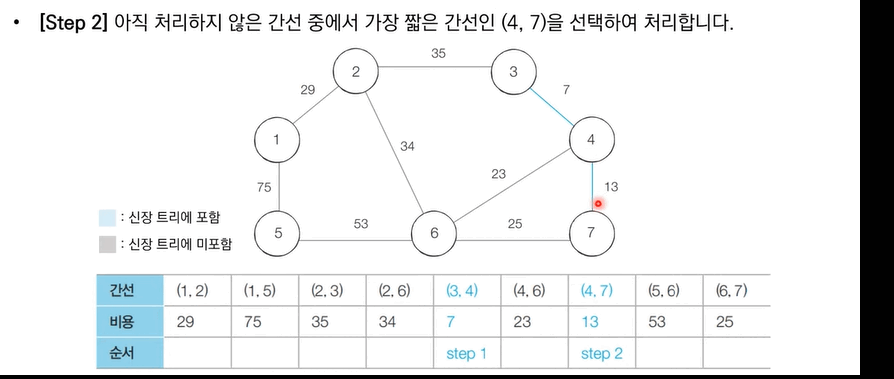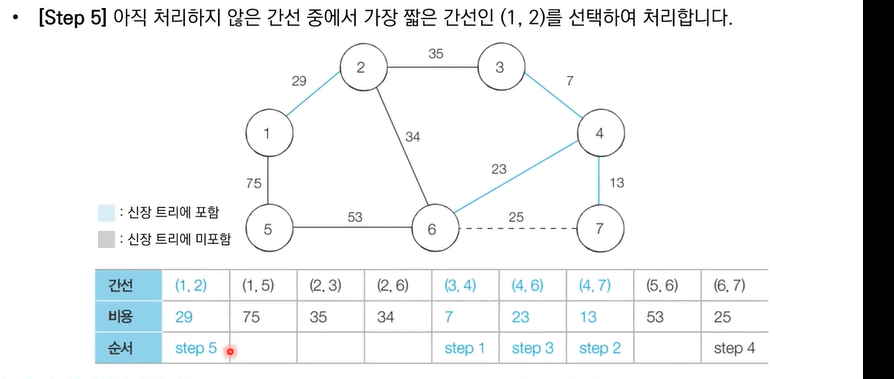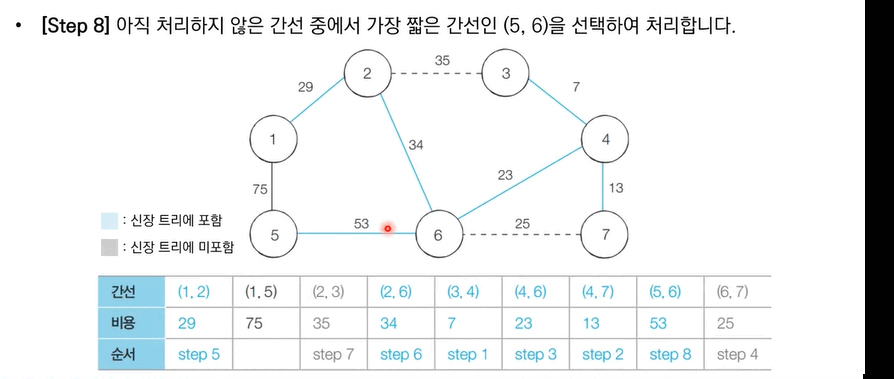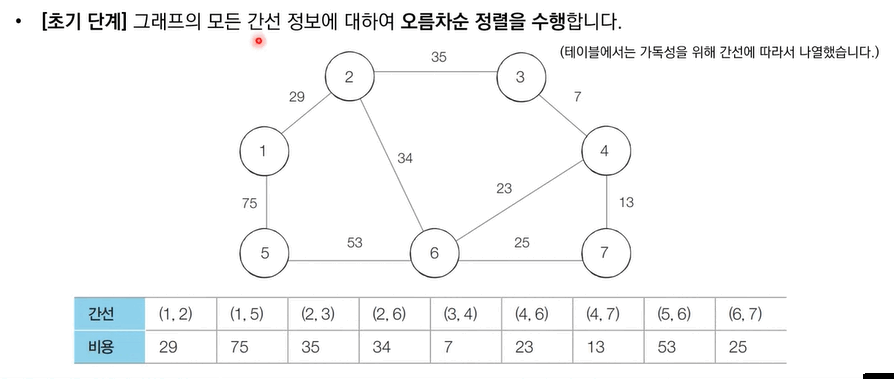
[Step 1]. 간선 데이터 비용에 따라 오름차순 정렬한다.
[Step 2]. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
[Step 3]. 사이클이 발생하지 않는 경우 최소 신장 트리에 포함한다.
[Step 4]. 사이클이 발생한다면 최소 신장 트리에 포함시키지 않는다.
[Step 5]. 모든 간선에 대하여 위 과정을 반복한다.

위 과정을 코드로 구현하면 다음과 같다.

function solution(n, costs) {
    let answer = 0;
    const parent = [];
    // 자기 자신의 값을 부모로 가지는 배열 생성
    for(let i=0; i<n; i++) parent.push(i);
    
    // 간선을 비용순으로 정렬
    costs.sort((a,b)=>a[2]-b[2]);
     
  	// 만약 초기 값이 아니라면 parent[x]를 이용해 위로 올라가서 부모값 찾음
    const getParent = (parent, x) => {
        if(parent[x] === x) return x;
        return parent[x] = getParent(parent,parent[x]);
    }
    
    // 두 부모중 작은 값을 가지는 부모로 합쳐준다.
    const unionParent = (parent, x, y) => {
        const n1 = getParent(parent,x);
        const n2 = getParent(parent,y);
        if(n1<n2) return parent[n2] = n1;
        else return parent[n1] = n2;
    }
    
    // 부모를 찾고, 부모가 같으면 true, 다르면 false return
    const findParent = (parent, x, y) => {
        const n1 = getParent(parent,x);
        const n2 = getParent(parent,y);
        if(n1===n2) return true;
        else return false;
    }
    
    for(const cost of costs){
        // 사이클이 발생하지 않는 경우에만 집합에 포함
        if(!findParent(parent,cost[0],cost[1])){
            answer += cost[2];
            unionParent(parent,cost[0],cost[1]);
        }
    }
    return answer;
}