Recursive Function
정의 단계에서 자신을 재참조하는 함수
재귀 함수(Recursive Function)는 자기 자신을 다시 재호출하는 함수를 의미한다.
대표적인 재귀 함수의 특징은 다음과 같다.
-
재귀 함수를 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있다.
-
모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있다.
-
컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부의 스택 프레임에 쌓인다.
Example
아래 코드는 단순한 형태의 재귀함수 예제이다.
function recursive_function () {
console.log('재귀 함수를 호출합니다.');
recursive_function();
}
recursive_function();
recursive_function함수는 자기 자신을 계속해서 추가로 불러오기 때문에'재귀 함수를 호출합니다.'라는 문자열이 무한히 출력
종료 조건
위 예제 코드를 실행하면 콘솔을 출력하다 다음과 같은 오류 메시지가 표시된다.
RecursionError: maximum recursion depth exceeded while pickling an object
해당 메시지는 재귀의 최대 깊이를 초과했다는 오류이며, 따라서 재귀의 호출은 무한대로 진행할 수 없다.
그래서 재귀함수는 반드시 아래와 같은 종료 조건을 포함하여 작성해야 한다.
- 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시해야 한다.
- 종료 조건을 제대로 명시하지 않으면 함수가 무한히 호출될 수 있다.
Example
아래 코드는 종료 조건을 포함한 재귀 함수 예제이다.
function recursive_function(i) {
// 100번 호출됬을 때 종료되도록 종료 조건 명시
if (i === 100) return;
console.log(`${i}번째 재귀함수에서 ${i + 1}번째 재귀함수를 호출합니다.`);
recursive_function(i + 1);
console.log(`${i}번째 재귀함수를 종료합니다.`);
}
recursive_function(1);Factorial
Factorial은 1부터 n 까지 양의 정수를 차례대로 곱한 값이며 '!' 기호로 표기한다.

Factorial 은 다음과 같이 반복적으로 구현할 수 있다.
// 반복적으로 구현한 n!
function factorial_iterative(n) {
let result = 1;
for (let i = 0; i <= n; i++) {
if (i <= 1) result *= 1;
else result *= i;
}
return result;
};
console.log(factorial_iterative(3));또한 위에서 설명했듯 반복문과 재귀 함수는 서로 동일한 목적으로 사용될 수 있으며, 위 코드는 다음과 같이 재귀 함수를 사용하여 작성할 수 있다.
// 재귀적으로 구현한 n!
function factorial_recursive(n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
};
console.log(factorial_recursive(3));최대공약수 (유클리드 호제법)
유클리드 호제법은 두 자연수의 최대공약수를 구하는 대표적인 알고리즘이다.
Euclidean algorithm
두 자연수 A, B에 대하여(A > B) A를 B로 나눈 나머지를 R이라고 한다.
이때 A와 B의 최대공약수는 B와 R의 최대공약수와 같다.
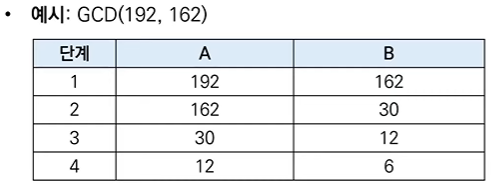
유클리드 호제법은 다음과 같이 재귀 함수로 작성할 수 있다.
function gcd(a, b) {
if (a % b === 0) return b;
else return gcd(b, a % b);
};
console.log(gcd(192, 162));// 실행결과
6
