Graph and Full Search
자료구조에서 말하는 그래프는 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 의미한다.
관계는 직접, 간접적으로 나뉘며 각각의 관계는 두 점 사이를 이어주는 선인 실선과 점선으로 구분된다.
이렇게 연결된 선은 그래프에서 간선(edge)이라 표현된다.
그래프의 탐색은 하나의 정점(vertex)에서 시작하여 그래프의 모든 정점들을 한 번씩 탐색하는 것이 목적이고 이를 완전탐색이라 부른다.
그 중 DFS와 BFS는 대표적인 정점 탐색 방법이다.
DFS(Depth-First Search)
깊이를 우선으로 탐색하는 탐색 방법
DFS는 깊이 우선 탐색이라고도 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
DFS는 Stack(혹은 재귀 함수)를 이용하며, 구체적인 동작 과정은 다음과 같다.

- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 더이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
Example
DFS를 Stack을 이용하여 구현하면 다음과 같다.
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
function DFS(graph, startNode) {
const visited = []; // 탐색한 노드를 담기 위한 배열
let stack = []; // 탐색을 위한 스택 배열
stack.push(startNode);
while (stack.length !== 0) { // 스택이 비워질 때까지 반복
const node = stack.pop();
// 스택의 마지막 노드를 탐색한 적이 없다면 해당 노드의 자식 노드들을 스택에 추가
if (!visited.includes(node)) {
visited.push(node);
stack = [...graph[node], ...stack];
}
}
return visited;
}
console.log(DFS(graph, 'A'));BFS(Breadth-First Search)
너비를 우선으로 탐색하는 탐색 방법
BFS는 너비 우선 탐색이라고도 부르며, 그래프에서 가장 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
BFS는 Queue 자료구조를 이용하며, 구체적인 동작 과정은 다음과 같다.
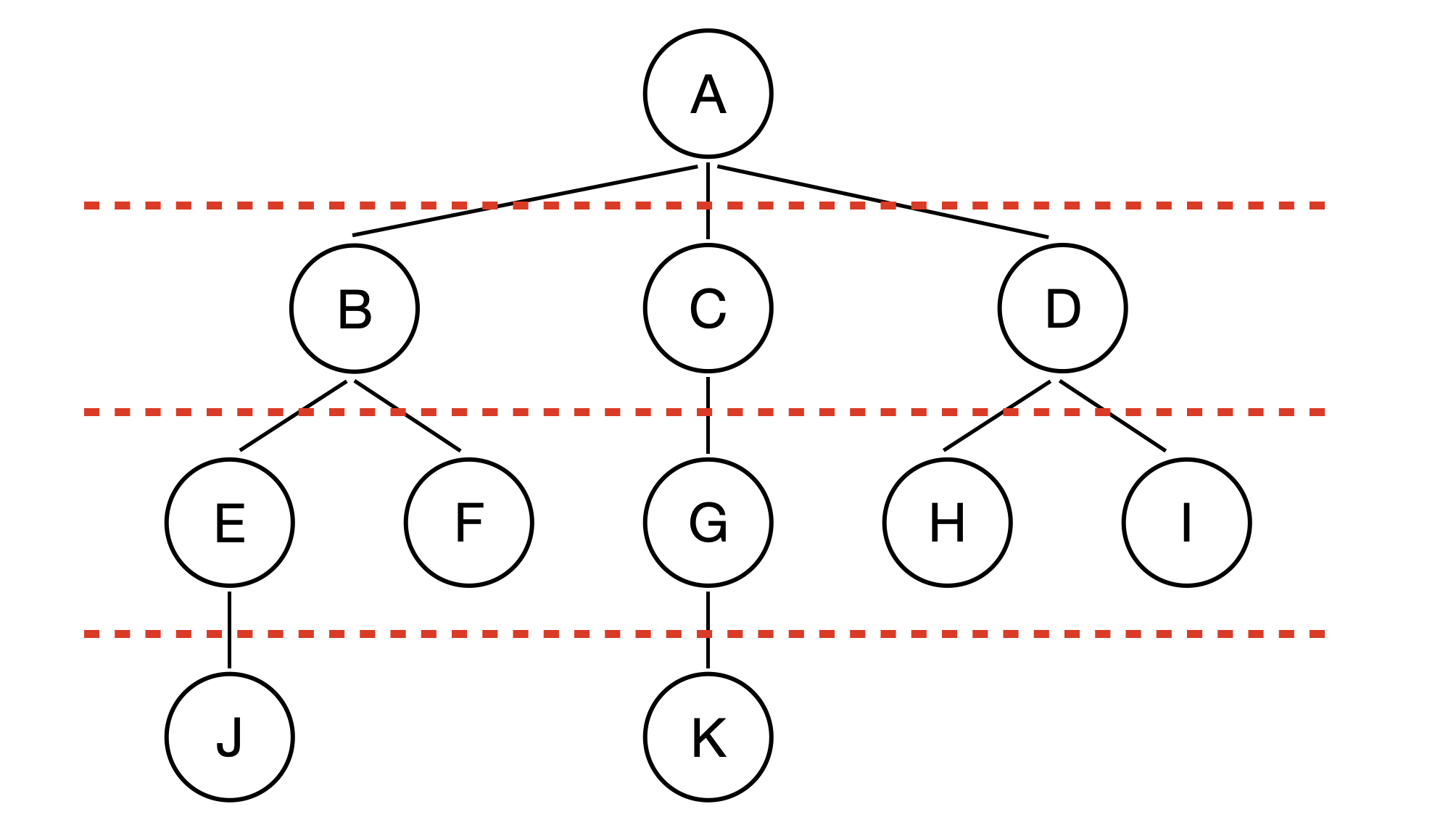
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
- 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
Example
BFS를 Queue를 이용하여 구현하면 다음과 같다.
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
function BFS(graph, startNode) {
const visited = []; // 탐색한 노드를 담기 위한 배열
let queue = []; // 탐색을 위한 큐 배열
queue.push(startNode);
while (queue.length !== 0) { // 큐가 비워질 때까지 반복
const node = queue.shift();
// 큐의 첫번째 노드를 탐색한 적이 없다면 해당 노드와 같은 레벨의 노드들을 큐에 추가
if (!visited.includes(node)) {
visited.push(node);
queue = [...queue, ...graph[node]];
}
}
return visited;
}
console.log(BFS(graph, 'A'));Problem 1, 음료수 얼려 먹기
N X M 크기의 얼음 틀이 있으며, 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시된다.
구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주한다.
이 때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하시오.
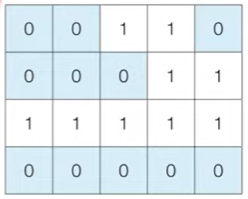
다음의 4 X 5 얼음 틀 예시에서는 아이스크림이 총 3개 생성된다.

Explanation
해당 문제는 DFS 혹은 BFS로 해결할 수 있다.
얼음을 얼릴 수 있는 공간이 상, 하, 좌, 우로 연결되어 있다고 표현할 수 있으므로 그래프 형태로 모델링 할 수 있다.
DFS를 활용하는 알고리즘은 다음과 같다.
- 특정 지점의 주변
상, 하, 좌, 우를 살펴본 뒤에 주변 지점 중에서 값이 '0'이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.- 방문한 지점에서 다시
상, 하, 좌, 우를 살펴보면서 방문을 진행하는 과정을 반복하면, 연결된 모든 지점을 방문할 수 있다.- 모든 노드에 대하여 1 ~ 2번의 과정을 반복하며, 방문하지 않은 지점의 수를 카운트한다.
const [N, M] = [4, 5];
const graph = [
[0, 0, 1, 1, 0],
[0, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0],
];
// DFS로 특정 노드를 방문 및 연결 노드들 방문
function dfs(x, y) {
// 주어진 범위를 벗어나는 경우에는 종료
if (x <= -1 || x >= N || y <= -1 || y >= M) return false;
if (graph[x][y] === 0) { // 현재 노드를 아직 방문하지 않았다면 방문 처리
graph[x][y] = 1;
// 상, 하, 좌, 우 위치를 모두 재귀적으로 호출
dfs(x - 1, y);
dfs(x, y - 1);
dfs(x + 1, y);
dfs(x, y + 1);
return true;
}
return false;
}
let result = 0;
for (let i = 0; i < N; i++) {
for (let j = 0; j < M; j++) {
if (dfs(i, j)) result++;
}
}
console.log(result);
