알고리즘) Knapsack 알고리즘

✏️ Knapsack 알고리즘

• Knapsack 알고리즘은 각 물건 i의 무게 wi와 가치 vi가 주어진 n개의 물건과 용량이 c인 가방이 있을 때, 배낭에 담을 수 있는 물건의 최대 가치를 찾는 문제이다.
• 이 때 물건은 쪼갤 수 없으며, 쪼갤 수 있는 경우 그리디 알고리즘으로 해결하면 된다.

1. Knapsack 알고리즘 해결 방법

(1) Knapsack 알고리즘의 부분 문제 - 1

• Knapsack 알고리즘은 물건, 물건의 무게, 물건의 가치, 배낭의 용량 총 4가지의 요소가 있다.
• 배낭이 비어있는 상태에서 시작해 물건을 하나씩 배낭에 담거나 안 담는 것을 현재 배낭에 들어있는 물건의 가치 합에 근거해 결정해야 하기 때문에 물건과 물건의 무게가 부분 문제를 정의하는데 고려된다.
• 또한 물건을 배낭에 담으려고 할 경우 배낭 용량의 초과 여부를 검사해야 한다.

(2) Knapsack 알고리즘의 부분 문제 - 2

• 배낭 문제의 부분 문제는 아래와 같이 정의할 수 있다.

  K[i, w] = 물건 1~i까지 고려하고, 배낭의 임시 용량을 w라고 했을 때 최대 가치
  (단, i = 1, 2, ..., n이고 w = 1, 2, ..., c이다)

• 부분 문제를 위와 같이 정의했을 때 최적해는 K[n, c]이다.

(3) Knapsack 알고리즘의 풀이 방법

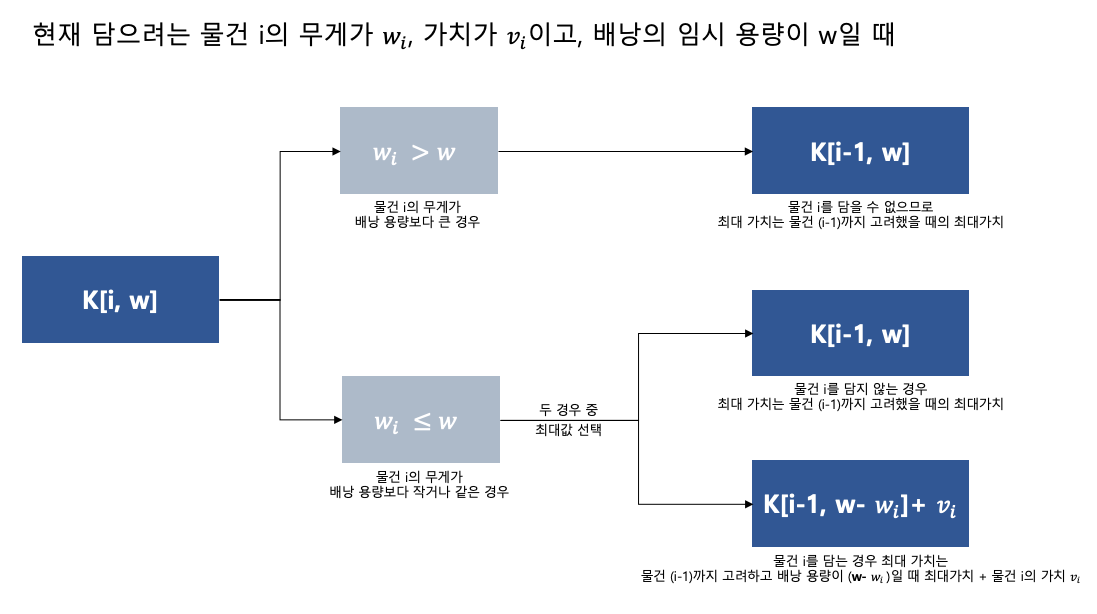
① 현재 담으려는 물건 i의 무게가 wi이고, 배낭의 임시 용량이 w일 때 두 가지의 경우가 있다.

• 물건 i를 배낭에 담을 수 있는 경우 : 물건 i의 무게 wi가 현재 배낭의 용량 w보다 같거나 작을 때
• 물건 i를 배낭에 담을 수 없는 경우 : 물건 i의 무게 wi가 현재 배낭의 용량 w보다 클 때

② 물건 i를 배낭에 담을 수 있는 경우는 다시 두 가지의 경우로 나눌 수 있다.

• 물건 i를 배낭에 담지 않는 경우
• 물건 i를 배낭에 담는 경우

→ 둘 중 더 큰 값을 K[i, w]로 설정해야 최대 가치를 구할 수 있다.

🧹 정리하자면!

(4) Knapsack 알고리즘의 수행 과정

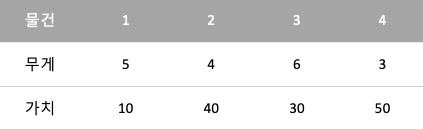
• 배낭의 용량 c는 10이고 각 물건의 무게와 가치는 다음과 같다.
  

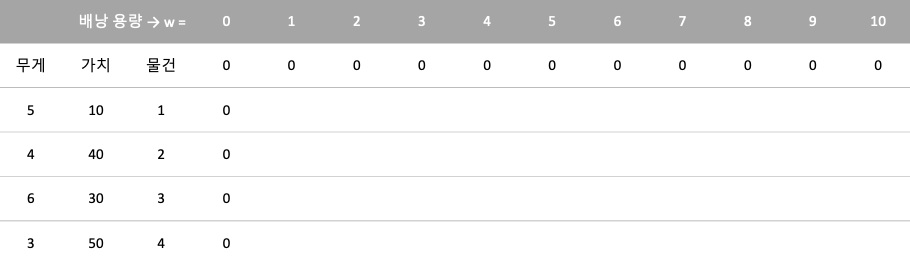
① 배열의 0번째 행과 0번째 열의 각 원소를 0으로 초기화 한다.

② 물건 1을 고려할 때

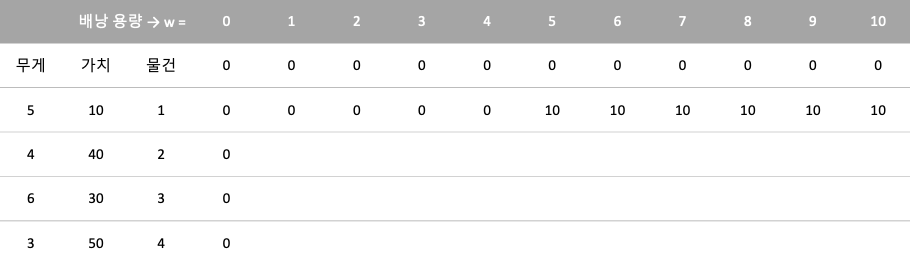
• w = 1, 2, 3, 4일 때 각각 wi > w이므로 물건 1을 담을 수 없다.
  • 따라서 각각 K[i, w] = K[i-1, w]으로 0이다.
• w = 5일 때 wi = w이므로 물건 1을 담을 수 있다.
  • 따라서 K[1, 5] = max(K[0, 5], K[0, 0]+10) = max(0, 10)으로 10이다.
• w = 6, 7, 8, 9, 10일 때 각각 wi < w이므로 물건 1을 담을 수 있다.
  • 따라서 각각 K[i, w] = max(K[i-1, w], K[i-1, w-wi]+vi)으로 10이다.

③ 물건 2를 고려할 때

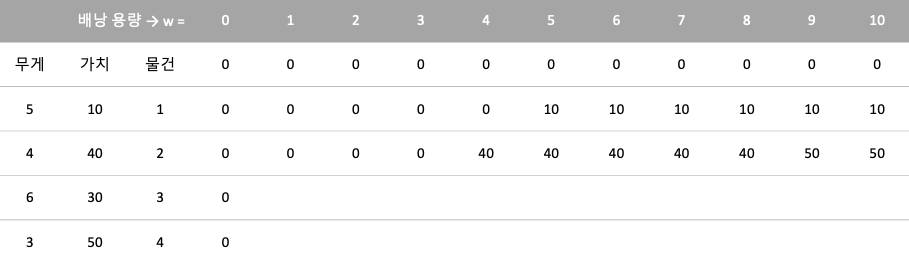
• w = 1, 2, 3일 때 각각 wi > w이므로 물건 1을 담을 수 없다.
  • 따라서 각각 K[i, w] = K[i-1, w]으로 0이다.
• w = 4일 때 wi = w이므로 물건 1을 담을 수 있다.
  • 따라서 K[2, 4] = max(K[1, 4], K[1, 0]+40) = max(0, 40)으로 40이다.
• w = 5일 때 wi < w이므로 물건 1을 담을 수 있다.
  • 따라서 K[2, 5] = max(K[1, 5], K[1, 1]+40) = max(10, 40)으로 40이다.
  • 즉, 물건 1을 배낭에서 빼낸 후, 물건 2를 담는다. 이 때 가치가 40이다.
• w = 6, 7, 8일 때 wi < w이므로 물건 1을 담을 수 있다.
  • 이 경우도 물건 1을 빼내고 물건 2를 배낭에 담는 것이 더 큰 가치를 얻는다.
  • 따라서 각각 K[i, w] = max(K[i-1, w], K[i-1, w-wi]+vi) = K[i-1, w-wi]+vi으로 40이다.
• w = 9일 때 각각 wi < w이므로 물건 1을 담을 수 있다.
  • 따라서 K[2, 9] = max(K[1, 9], K[1, 5]+40) = max(10, 50)으로 50이다.
  • 즉, 이 경우 물건 1과 2를 다 담을 수 있고, 이 때 가치가 50이다.
• w = 9일 때는 w = 10일 때와 같다.

④ 최종

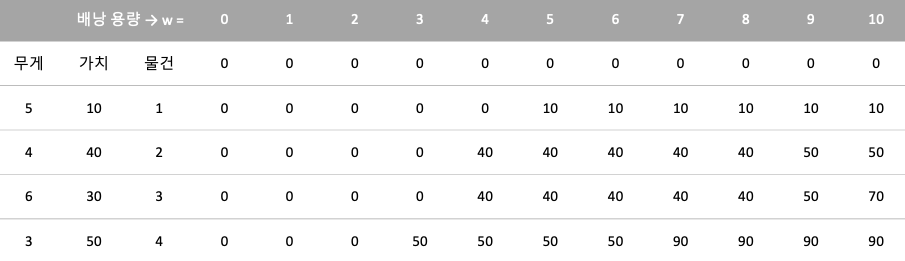
• 같은 방법으로 i=3, i=4일 때 알고리즘이 수행을 마친 결과이다.
• 우리가 구하고자 한 최적해는 K[4, 10]이고 이 값은 물건 2와 4의 가치의 합인 90이다.

2. Knapsack 알고리즘 구현 (Python)

# N : 물건의 개수, C : 최대 용량
N, C = map(int, input().split())
graph = [[0,0]] # 물건이 아무것도 포함되지 않은 초기 상태 설정

for i in range(N): 
    # 물건 배열에 각 물건의 무게와 가치 추가
    graph.append(list(map(int, input().split())))

# 행 : 물건의 개수+1, 열 : 무게+1인 표를 0으로 초기화
dp = [ [0]*(C+1) for _ in range(N+1) ]
 
for item in range(1, N+1): # 행
    for wi in range(1, C+1): # 열
        
        weight = graph[item][0] # 현재 물건의 가치
        value = graph[item][1] # 현재 물건의 무게
 
        if (wi < weight): # 현재 물건이 배낭의 임시 최대 용량보다 클 때
            # 물건을 넣지 않는다. 최대 가치는 이전 물건까지 고려했을 때의 최대 가치
            dp[item][wi] = dp[item-1][wi] 
        else: 
            # 더 나은 경우를 찾는다. 
            # S1. 현재 물건을 넣지 않는다.
            # 최대 가치는 이전 물건까지 고려했을 때의 최대 가치
            # S2. 현재 물건을 넣는다.
            # 최대 가치는 이전 물건까지 고려하고, 임시 최대 용량이 현재 무게-물건의 무게 일때의 최대 가치에 물건의 가치를 더한 값
            dp[item][wi] = max(dp[item-1][wi], dp[item-1][wi-weight] + value)
 
print(dp[N][C])