Intro
- 3월 2주차는 이런 저런 이유로 못했다...(핑계)
- 이번주는 회피하게 되는 유형인 DP 문제를 아주 쉬운 문제부터 풀이해봤다.
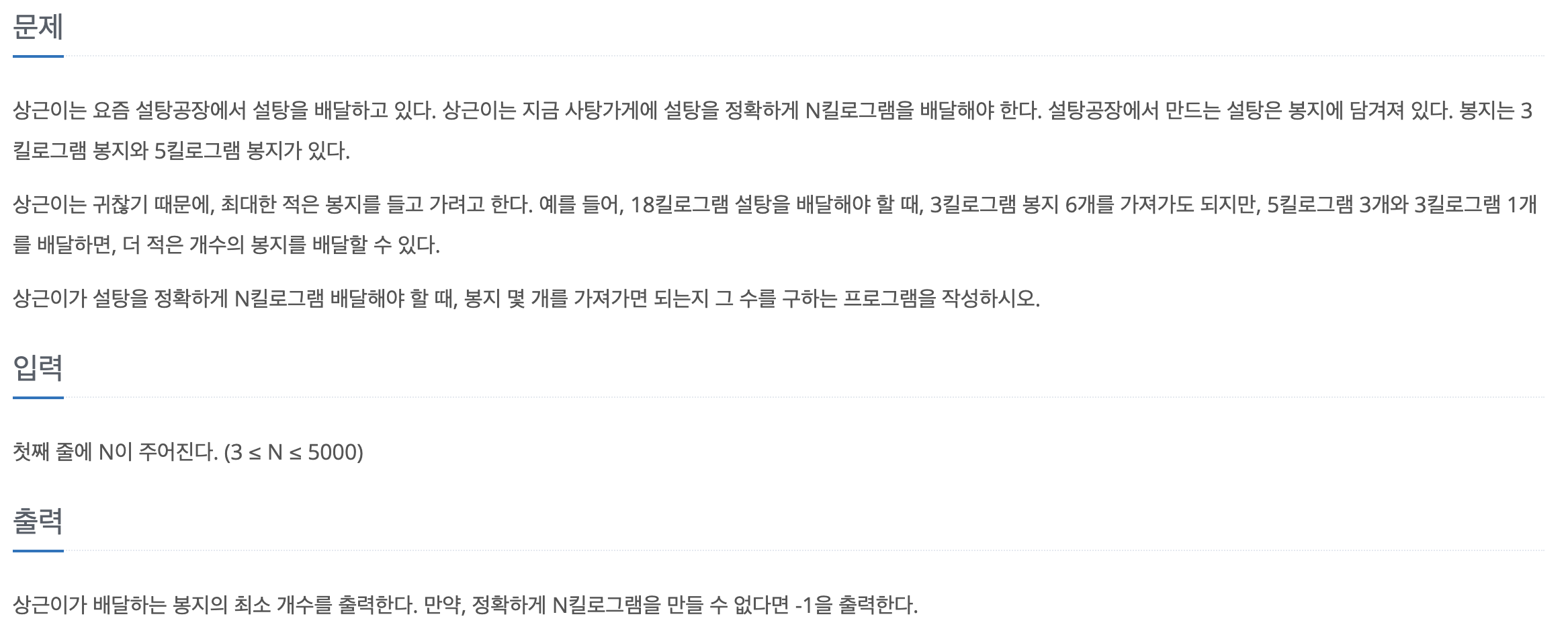
2839번 설탕 배달
https://www.acmicpc.net/problem/2839
풀이 과정
- 어떻게 식을 세워야 할 지 모르겠어서 무작정 3부터 18까지 손으로 써보면서 규칙을 찾았다.
- i kg 일 때의 설탕 봉지 갯수는
- (i-3)kg 일 때의 설탕 봉지 갯수 + 1
- (i-5)kg 일 때의 설탕 봉지 갯수 + 1
- 두 가지 경우가 있다. 봉지의 최소 개수를 출력해야 하므로 두 값 중 작은 값을 i kg일 때 설탕 봉지 갯수로 결정한다.
- 처음에 dp의 값들을 봉지의 예상 최대 갯수보다 크게 설정해 그 값 이상인 경우는 정확한 갯수를 구할 수 없는 경우이므로 -1을 출력하도록 한다.
정답 코드
N = int(input())
d = [5001] * (N+3)
d[3] = 1
d[5] = 1
for i in range(6, N+1) :
d[i] = min(d[i-3]+1, d[i-5]+1)
if d[N] >= 5001:
print(-1)
else:
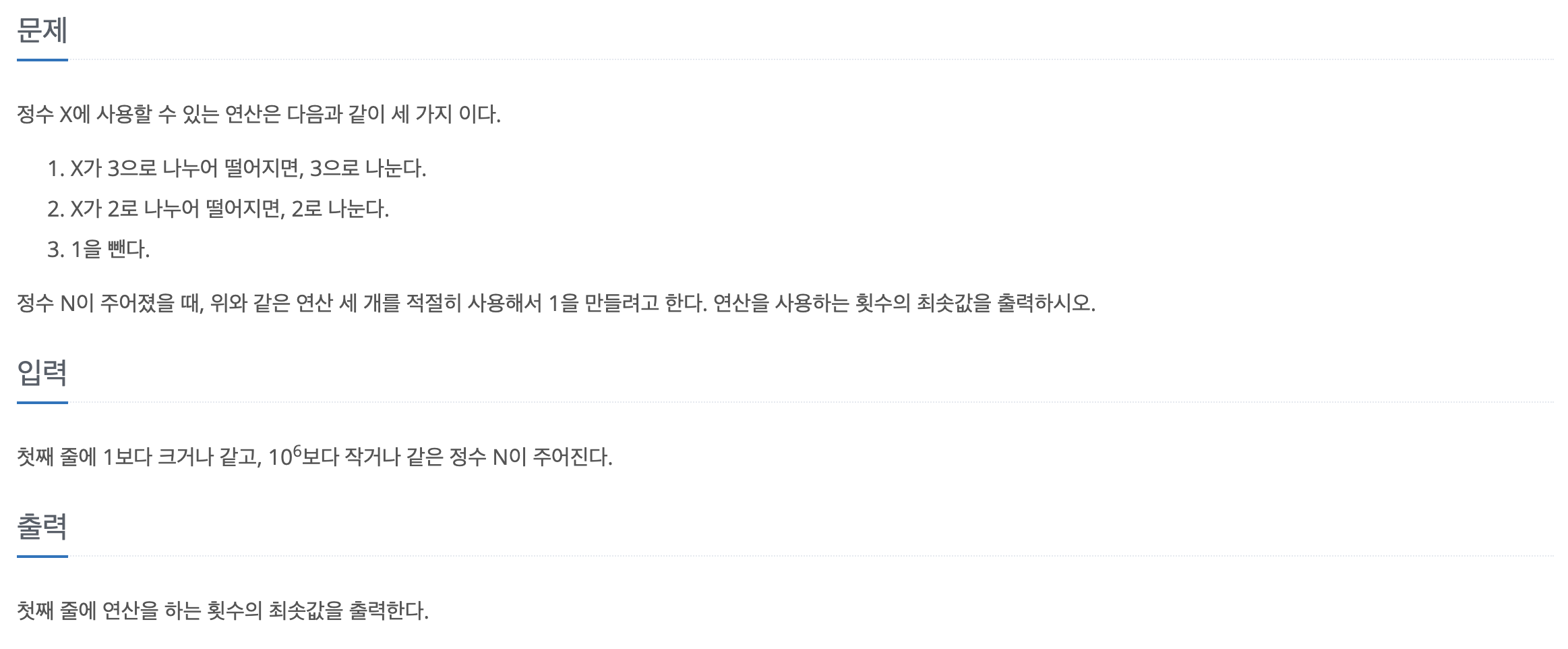
print(d[N])1463번 1로 만들기
https://www.acmicpc.net/problem/1463
풀이 과정
- 이 문제도 감이 안잡혀서 1부터 18까지 손으로 써봤다..ㅎ
- 손으로 쓰다보니 숫자별로 3번만 되는 경우도, 1번이나 2번과 3번이 되는 경우도, 1~3번이 모두 되는 경우도 있었다.
- 작은 값부터 dp 값을 구해서 큰 수에서 그 값을 이용할 수 있게 했다.
- ex) X가 18인 경우 : dp[6], dp[9], dp[17] 중 가장 작은값 + 1이 dp[18] 값이 된다.
- 3번은 모든 수가 해당되므로 우선 dp[i-1] + 1을 dp[i] 값으로 설정하고, 3으로 나누어지는 경우(dp[i//3]+1)와 2로 나누어지는 경우(dp[i//2]+1) 각각에 대해 dp[i]와 비교하며 최솟값을 구했다.
정답 코드
N = int(input())
d = [0] * (N+1)
for i in range(2, N+1):
d[i] = d[i-1] + 1
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)
if i % 2 == 0 :
d[i] = min(d[i], d[i//2] + 1)
print(d[N])2579번 계단 오르기
https://www.acmicpc.net/problem/2579

풀이 과정
- 잘 이해가 안가서 다른 풀이들을 참고했다.
- 만약 i번째 계단에 있다면 아래의 두 가지 경우가 존재하고, 두 값 중 큰 값을 dp[i]로 결정한다.
- i-1번째 계단에서 올라옴
- i-2번째 계단에서 올라옴
- i-1번째 계단에서 올라온 경우, 그 이전 계단은 i-3이므로
- dp[i] = score[i] + score[i-1] + dp[i-3] 이다.
- (아래 코드에서 score는 첫번째 계단이 score[0]이어서 1씩 더 빼줬다.)
- i-2번째 계단에서 올라온 경우
- dp[i] = score[i] + dp[i-2] 이다.
정답 코드
n = int(input())
score = []
for i in range(n):
score.append(int(input()))
if n == 1:
print(score[0])
else:
dp = [0]*(n+1)
dp[1] = score[0]
dp[2] = score[0] + score[1]
for i in range(3, n+1):
dp[i] = max(score[i-1]+score[i-2]+dp[i-3], score[i-1]+dp[i-2])
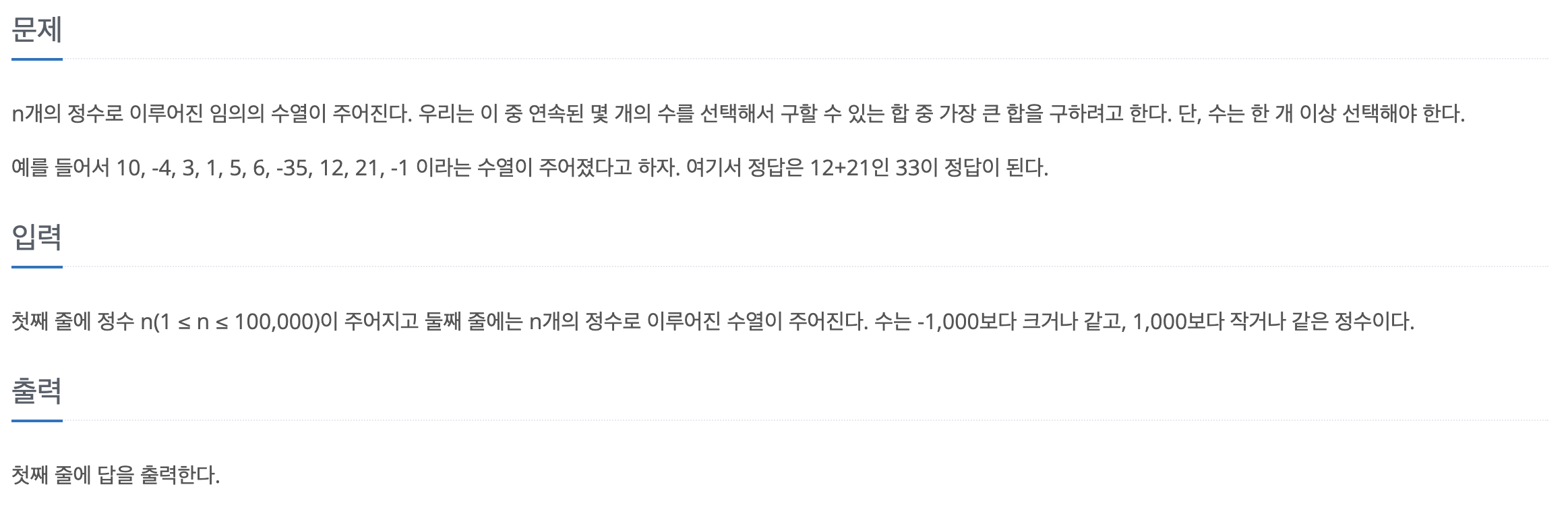
print(dp[n])1912번 연속합
https://www.acmicpc.net/problem/1912
풀이 과정
- 단순하게 i번째일 때 i값만 가지는 것과 i-1까지의 최댓값에 i를 더한 값 중 더 큰 값을 dp[i]값으로 정하고 가장 큰 dp값을 구하면 되겠다 생각하고 풀이했다.
정답 코드
n = int(input())
num = list(map(int, input().split()))
dp = [0] * n
dp[0] = num[0]
for i in range(1, n):
dp[i] = max(dp[i-1]+num[i], num[i])
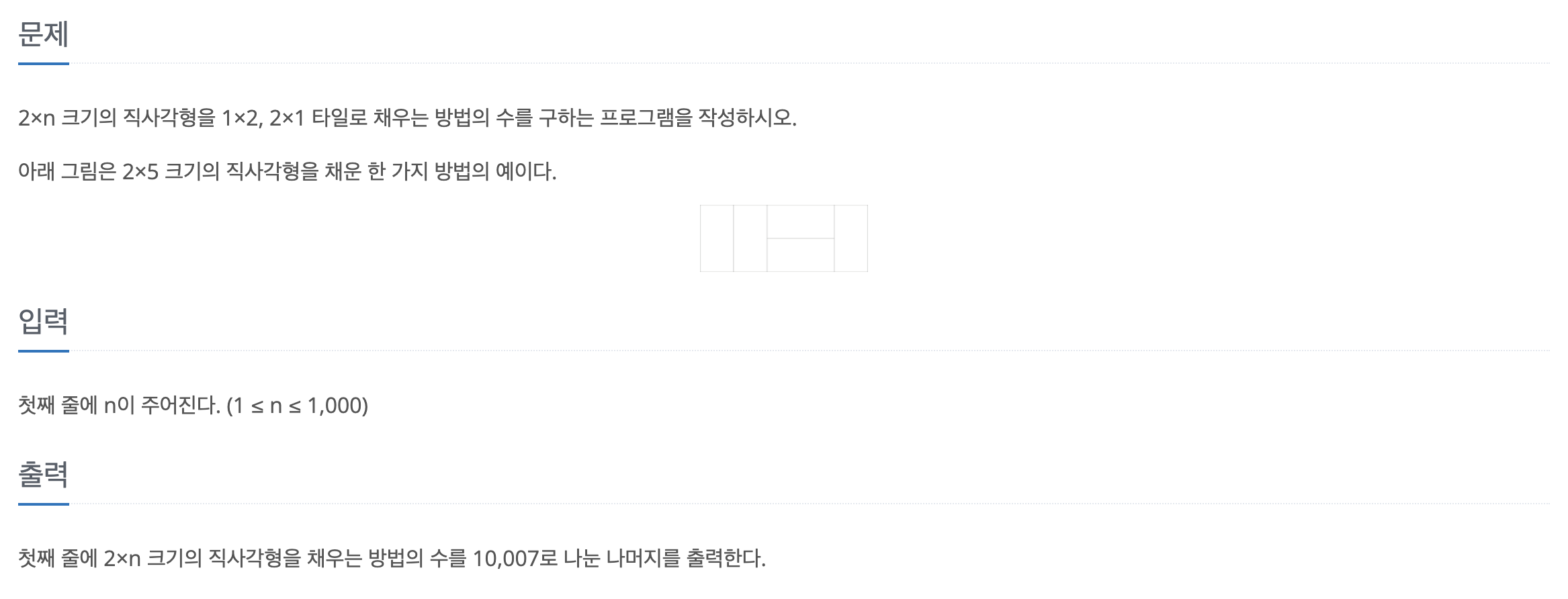
print(max(dp))11726번 2xn 타일링
https://www.acmicpc.net/problem/11726
풀이 과정
- 사실 이 문제는 예전에 풀었지만 다음 문제와 비교해보기 위해 작성한다.
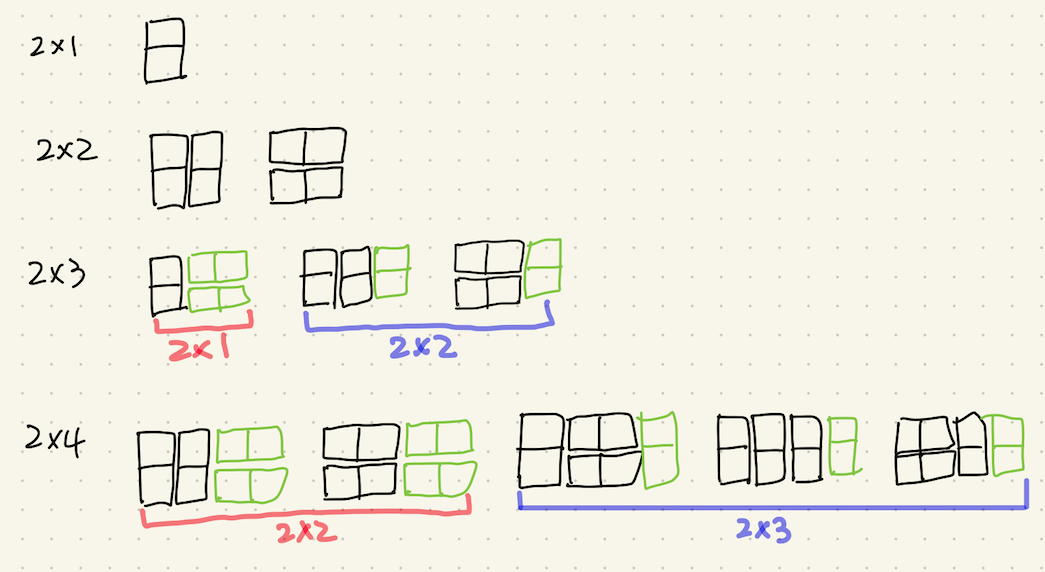
- n번째일 때 채우는 방법은 n-2번째 방법에 1x2 타일 두 개를 놓는 방법과 n-1번째 방법에 2x1 타일 한 개를 놓는 방법을 합친 것과 같다.
- 따라서 타일의 갯수는 tiles[n] = tiles[n-1] + tiles[n-2] 이다.
정답 코드
n = int(input())
tiles = [0]*1001
tiles[1] = 1
tiles[2] = 2
for i in range(3, n+1):
tiles[i] = tiles[i-1]+tiles[i-2]
print(tiles[n]%10007)11727번 2xn 타일링 2
https://www.acmicpc.net/problem/11727
풀이 과정
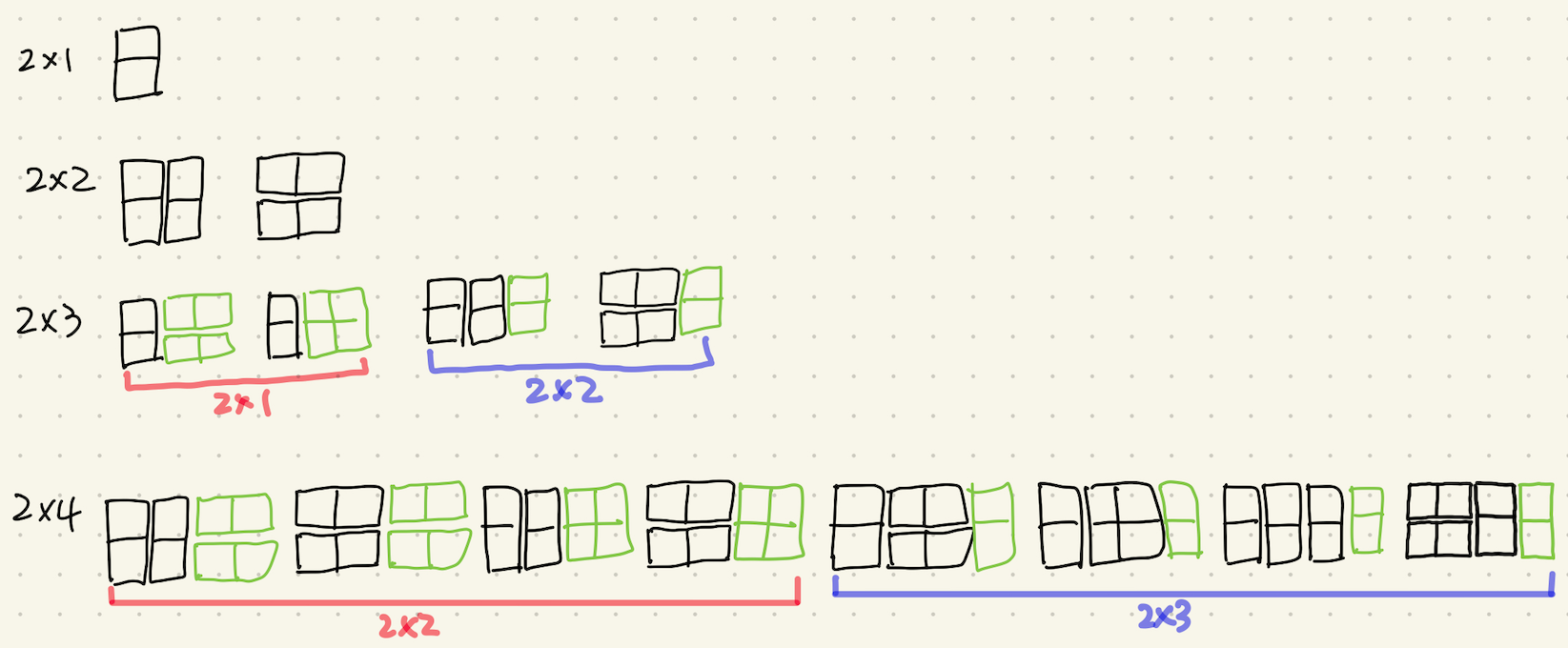
- 위의 문제와 비슷하지만 2x2 타일이 추가되었다. 위 문제와 구하는 방법도 동일하지만 2x2가 추가되어 n-2번째 방법에 1x2 타일 두 개를 놓는 것을 2x2로 대체하는 것을 추가한다.
- 따라서 타일의 갯수는 d[n] = 2 * d[n-2] + d[n-1] 이다.
정답 코드
n = int(input())
d = [0] * (n+1)
if n == 1:
d[1] = 1
print(d[1]%10007)
else:
d[1] = 1
d[2] = 3
if n == 2:
print(d[2]%10007)
else:
for i in range(3, n+1):
d[i] = 2*d[i-2] + d[i-1]
print(d[n]%10007)1890번 점프
https://www.acmicpc.net/problem/1890
풀이 과정
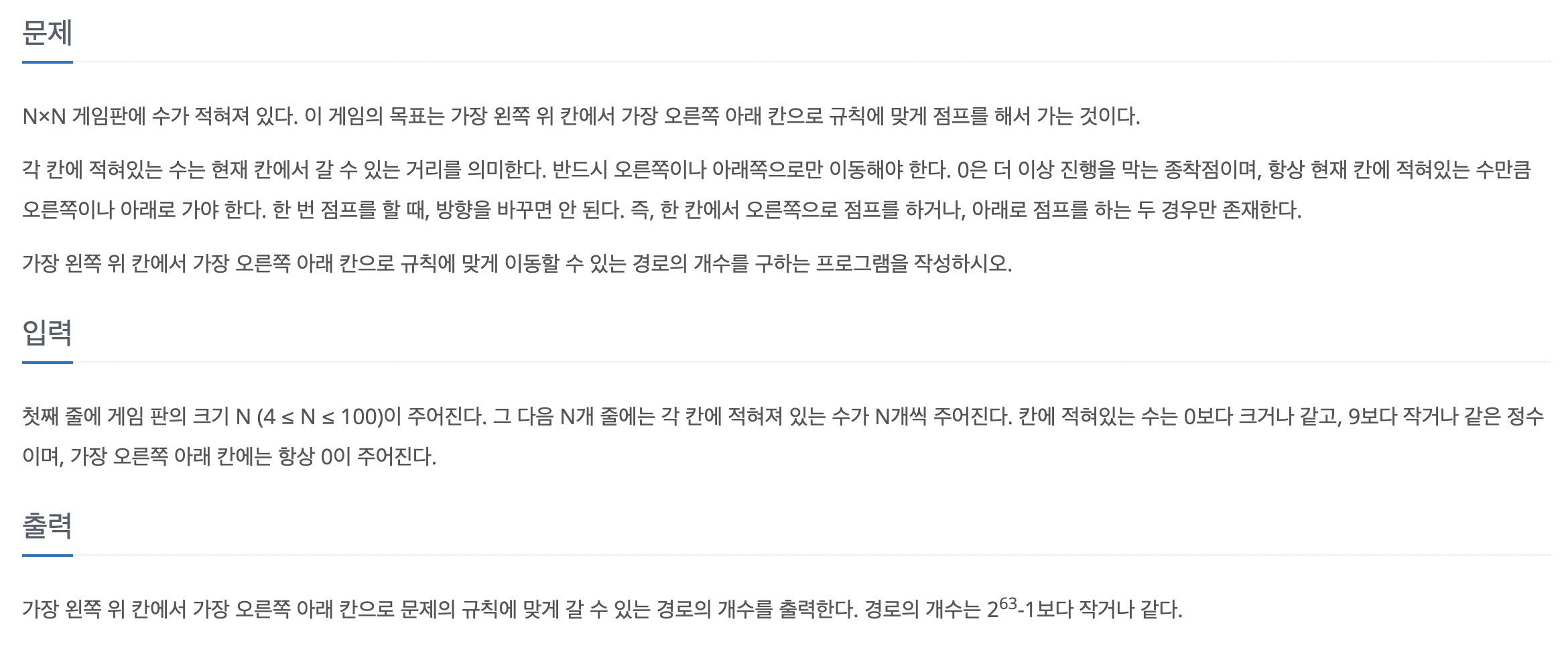
- 첫 칸의 dp값을 1로 설정한다.
- 첫 칸부터 모든 칸에 대해 반복문을 돌면서 해당 칸의 숫자만큼 각각 오른쪽과 아래쪽으로 이동할 수 있으면 이동할 수 있는 칸의 dp값에 현재 칸의 dp 값을 더해준다.
- 모든 칸을 돌고 마지막 칸(i==N-1, j==N-1)에 도착하면 반복문을 탈출하고 dp[N-1][N-1]을 출력한다.
정답 코드
N = int(input())
map = [list(map(int, input().split())) for i in range(N)]
dp = [[0] * N for i in range(N)]
dp[0][0] = 1
for i in range(N):
for j in range(N):
if i==N-1 and j==N-1:
break
right = j + map[i][j]
bottom = i + map[i][j]
if right < N:
dp[i][right] += dp[i][j]
if bottom < N:
dp[bottom][j] += dp[i][j]
print(dp[N-1][N-1])