[D&A DeepSession] 2차시 - 퍼셉트론,오차역전파법

공부보따리·2023년 6월 6일

D&A DeepSession

01.머신러닝

비용함수 ( Cost Function )

비용(cost)이란? -> 가설이 얼마나 정학환가를 판단하는 기준
비용함수
- 최적의 매개변수(prameter)를 찾게 만드는 '지표'
- 예측값과 실제값의 오차가 가장 작은 가설 함수?
- ex) $cost(W,b) = \frac{1}{N}\sum{}{}_{(x,y)\in D}(y - prediction(x))^2$
- 대표적인 비용함수 MSE
- $cost(w,b)$ 가 최소가 되는 W와 b를 구하는 것이 목표

선형회귀

선형회귀란? -> 데이터를 가장 잘 대변하는 최적의 선을 찾은 과정이다.
변수가 p인 선형회귀에서의 회귀식(p개의 특성이 있는 회귀식)
$\hat{y} = X\theta + bias$ ( $\theta \fallingdotseq W$ )
- $\theta$ 는 가중치 행렬 p X 1
- $X$ 는 input데이터 행렬 n X p
- $bias$ 는 편항 p X 1
최솟값을 구하면 비용이 최소! 방법은?
1. 그냥 냅다 미분 하기
2. 경사하강법

02.경사하강법

그냥 냅다 미분하기

$cost(W,b) = \frac{1}{N}\sum{}{}_{(x,y)\in D}(y - prediction(x))^2$
미분 결과 : $\hat{\theta} = (X^TX)^{-1}X^TY$ (선형회귀의 정규 방정식)

위의 식은 convex(볼록)하기 때문에 전역최소값을 갖는다 -> 식의 최솟값은 1개!!

❕ 전역최소값 : 한 손실 함수의 지역 최소값을 모아놓은 집합이 있다면 이 집합의 최소값

📌but, 행렬곱, 역행렬 계산은 X가 많다면 매우 어려우므로 보다 효율적으로 계산하기위해 한번에 미분하는 것이 아닌 차근차근 내려가는 방식인 경사하강법이 등장❗

경사하강법

경사하강법이란?
-> 한 지점에서 기울기를 구한 뒤, 기울기가 감소하는 방향으로 차근차근 내려가는 방법
-> 매개변수를 업데이트할 때, 비용함수의 기울기를 사용하여 현재 위치에서 가장 가파른 경사 하강 방향으로 이동
-> 최적화 과정에서 점진적으로 더 작은 손실 값을 구하는 반복적인(iterative)한 방법
Learning rate
-> 경사하강법에서 한걸음씩 움직일 때 얼마나 움직일지
-> 즉, 보폭
- learning rate가 지나치게 큰 경우 -> 최소값을 찾기 힘들다
- learning rate가 지나치게 작은 경우 -> 시간 多 $W := W - \alpha\frac{\sigma}{\sigma W}cost(W)$
- 위의 식은 W지점에서 미분한 기울기 $\alpha$ (=Learning rate)를 곱해 원래지점 W에 빼서 새로운 W를 업데이트 하는 식이다!!

03.인공신경망

퍼셉트론

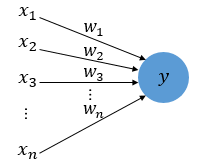
Frank Rosenblatt가 1957년에 제안한 초기 형태의 인공신경망
다수의 신호를 입력 받아, 하나의 결과를 출력하는 형태 ( = 다수의 입력 -> 하나의 출력)
다수의 입력 데이터를 넣어 신호가 일정 크기 이상이 되면 값을 출력
- $if \ \mathrm{\sum}_{k}^nW_ix_i +b \ge =0 \rightarrow y=1$
- $if \ \mathrm{\sum}_{k}^nW_ix_i +b < =0 \rightarrow y=0$

단층 퍼셉트론의 한계

선형분류만 가능 !
XOR 게이트 (같으면 0, 다르면 1 출력) 구현 불가능

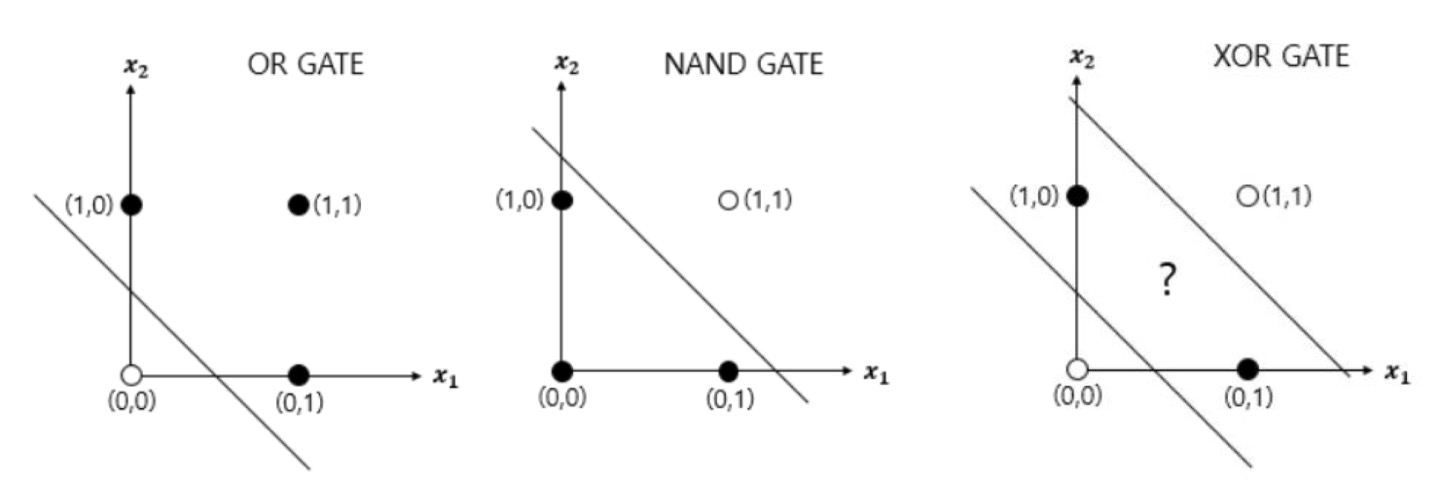
➕선형분류 : 직선하나로 2개의 영역을 나누는 것

Activation Function ( 활성화 함수 )

비선형 함수
ex ) sigmoid , ReLU ...
비선형성을 가해주는 역할로 선형분류기를 비선형 분류기로 변환 가능하다.
퍼셉트론은 선형결합 후 비선형 함수를 통과

MLP ( Multi Layer Perceptron )

퍼셉트론은 선형 결합만 진행

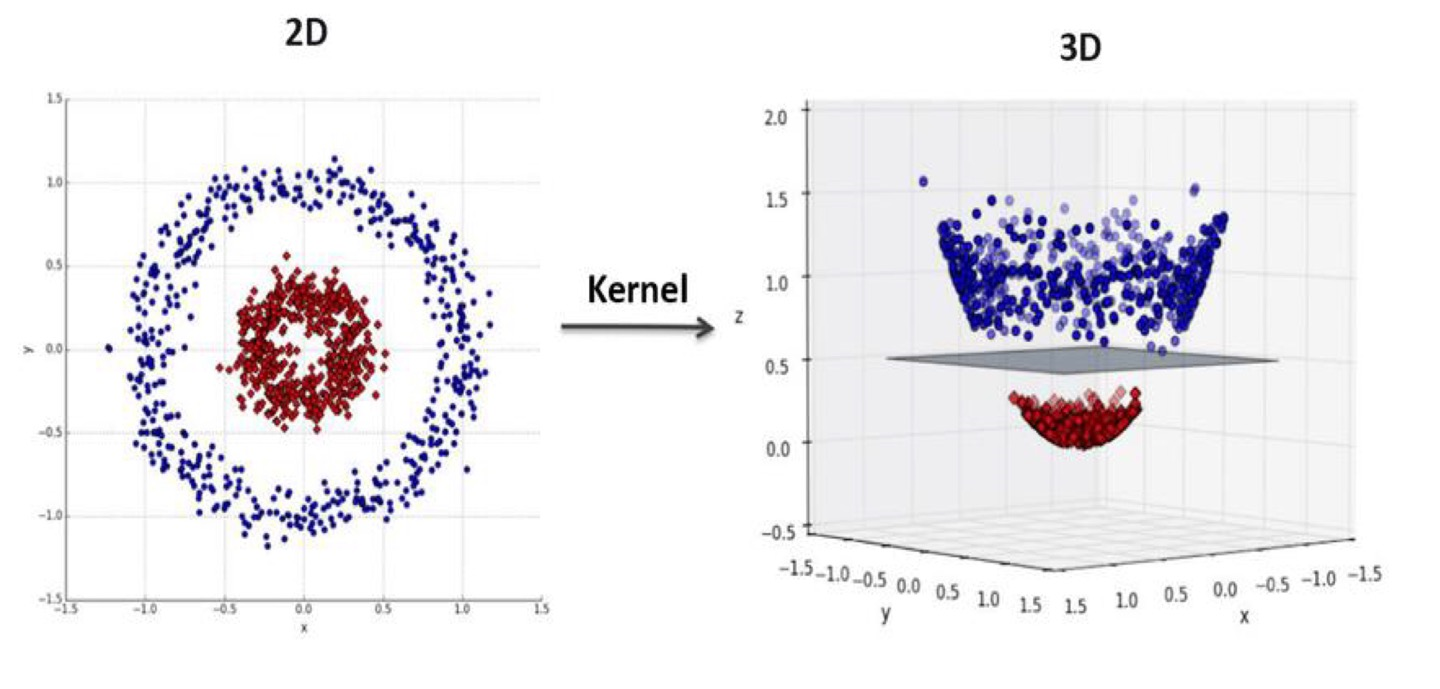
여러개의 퍼셉트론을 쌓아도 결국 하나에 퍼셉트론에서는 직선하나를 긋는 것,,, -> 그렇다면 시점을 바꿔보자 !

정의역 구간을 바꾸어(시점을 변환하여 ) 위의 그림처럼 2D에서는 선형으로 풀 수 없었던 문제들이 3D로 시점변환을 하면서 선형으로 풀수있게 변하기도 한다.

MLP

여러개의 Layer를 쌓아 올린 형태로 구성
비선형 분류가 어려운 단일 퍼셉트론의 한계점을 극복하기위해 등장
기본구조
- 입력층 (input layer)
- 은닉층 (hidden layer)
- 출력층 (output layer)
- 노드

04.오차역전파법

순전파와 역전파

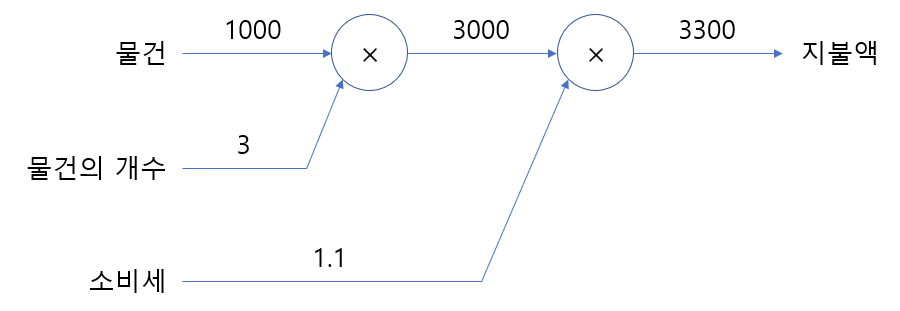
순전파 (Feed Forward, Forward Propagation)

MLP의 파라미터를 활용하여 결과값을 계산하는 방법
이전 layer에서 넘어온 값에 가중치(w = weight)와 편향(b = bias)를 적용해 다음 layer로 넘기는 방식
$\hat{y}$ 와 $y$ 를 비교하여 cost(오차)를 계산
출발점(왼쪽)에서 종착점(오른쪽)으로의 전파를 의미

역전파 (Backpropagation)

MLP의 파라미터를 업데이트하는 과정
순전파 과정을 통해 나온 cost(오차)를 활용하여 각 layer의 w와 b를 최적화 한다.
cost function이 최소화 되는 방향으로 w와 b를 수정
종착점(오른쪽)에서 출발점(왼쪽)으로의 전파를 의미 (순전파와 반대방향)

오차역전파법

가중치 매개변수의 기울기를 효율적으로 계산하는 방법.
연쇄법칙(chain rule)를 따른다.
- 연쇄법칙이란 ? "합성합수의 미분은 합성 합수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다." 는 합성함수의 미분에 대한 성질
- 역전파에서 '국소적 미분'을 전달하는 원리는 연쇄법칙을 따른다.
📌국소적 계산 : 전체에서 어떤 일이 일어나든 자신과 관계된 정보만을 사용하는 것
덧셈노드의 역전파
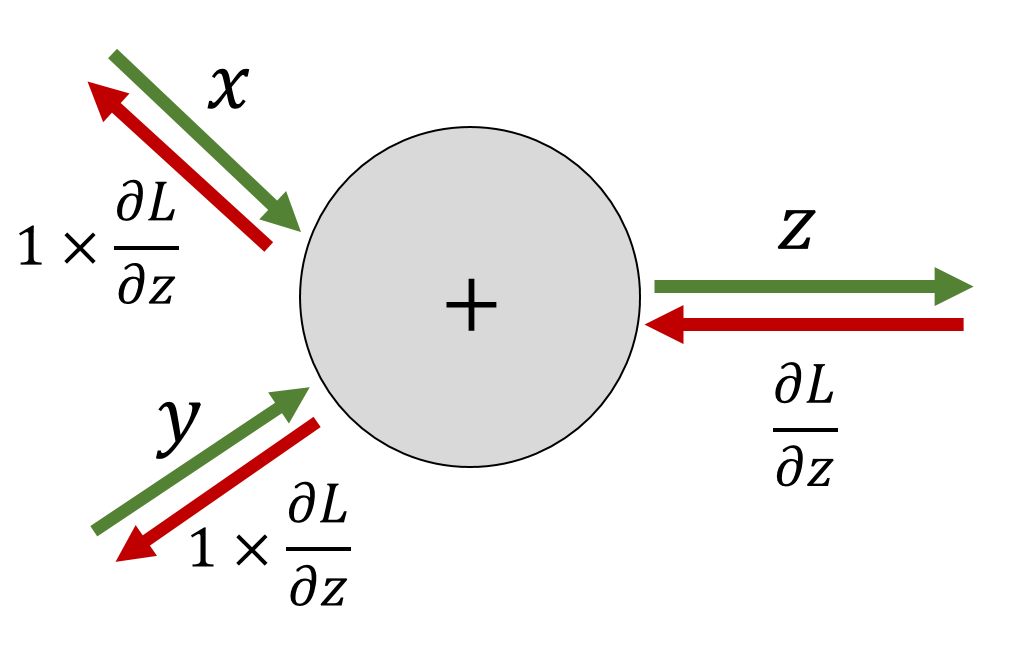
- 입력값을 그대로 흘려보냄.
- 순전파의 입력신호의 값은 필요하지 않음.
곱셈노드의 역전파
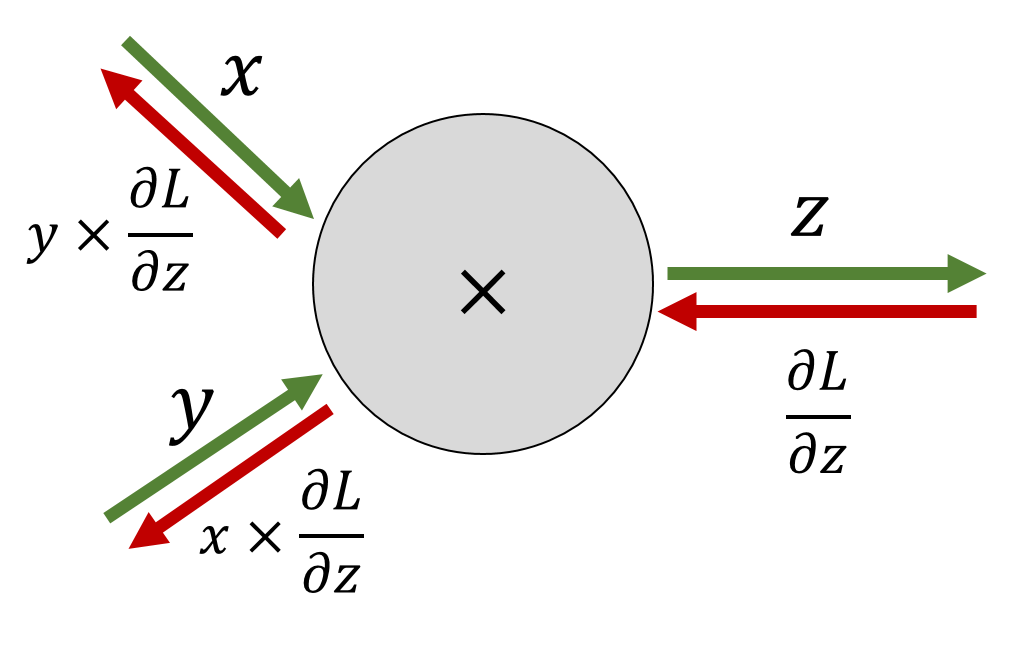
- 상류값에 순전파에서의 입력신호들을 서로 바꾼 값을 곱해서 하루로 흘려보냄.
- 순전파의 입력신호의 값이 필요함.
- 이를 위해 곱셈노드를 구현 할 때 순전파의 입력 신호를 변수에 저장함.