Score Matching

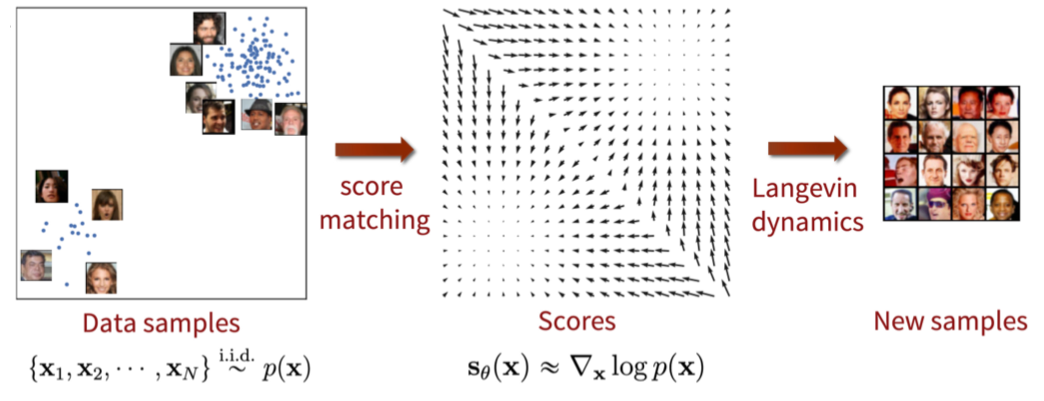
• first proposed in [Hyvarinen, 2005]
• concept : match the scores of data and model distribution $s_{\theta}(x) \approx \nabla_{x} \ log \ p(x)$
  - However, we don’t know the scores of data distribution
  - Instead, use the equivalent form
  $\frac{1}{2}\mathbb{E}_{x\sim p(x)}[||s_{\theta}(x) - s_{\mathrm{data}}(x)||_{2}^{2}] = \mathbb{E}_{x\sim p(x)} \ \left[\mathrm{tr}(\nabla_{x}s_{\theta}(x))\ +\ \frac{1}{2}||s_{\theta}(x)||_{2}^{2}\right]\ + \ \mathrm{const.}$
• Proof (TODO)
• 수식 설명
  • 우변의 계산을 통해서 true score에 접근하지 않고도 score network를 그것과 거의 같아지게 만들 수 있다
  • data dimension이 커짐에 따라 $tr(\nabla_{x} \ s_{\theta}(x))$의 계산량이 크게 늘어나기 때문에 not scalable

Denoising score matching

• $tr(\nabla_{x} \ s_{\theta}(x))$ 계산을 우회하는 score matching 방법
• 먼저 data point $x$를 pre-specified noise distribution $q_{\sigma}(\tilde{x}|x)$으로 perturb한다
• 그런 다음 true data distribution $p_{data}(x)$가 아닌 perturbed data distribution $q_{\sigma}(\tilde{x}) \triangleq \int \ q_{\sigma}(\tilde{x}|x)p_{data}(x)dx$ 를 score matching한다
• Objective
  $\frac{1}{2}\mathbb{E}_{q_{\sigma}(\tilde{x}|x)p_{data}(x)}[||s_{\theta}(\tilde{x})-\nabla_{\tilde{x}}\mathrm{log}\ q_{\sigma}(\tilde{x}|x)||^{2}_{2}]$
• Proof (TODO)
• 이 방법대로 하면 nabla 안의 계산이 간단해져서 score matching 가능
• 그러나 $q_{\sigma}(x)$와 $p_{data}(x)$의 score가 같다는 가정을 유지하려면 noise가 충분히 작아야 한다

Sliced score matching

• $tr(\nabla_{x} \ s_{\theta}(x))$을 approximate하기 위해 random projections를 이용하는 방법
• Objective
  $\mathbb{E}_{p_{v}}\mathbb{E}_{p_{data}}[v^{T}\nabla_{x}s_{\theta}(x)v\ +\ \frac{1}{2}||s_{\theta}(x)||^{2}_{2}]$
• $p_v$ : simple distribution of random vectors
  • e.g. multivariate standard normal
• 원래 score matching objective에서 trace 계산을 $v^{T}\nabla_{x}s_{\theta}(x)v$ 로 바꾼 것
  • forward mode auto-differentiation을 통해 빠르게 계산 가능
  • denoising score matching보다 4배 이상 많은 계산량
• 장점: perturbation 없이 원래 data distribution의 score를 구할 수 있음

어떻게 활용할까?

• Langevin dynamics를 이용해 iterative하게 새로운 데이터를 sampling할 수 있다
• 많은 계산량 때문에 실제로 적용하기 어려워서 잘 안 쓰이다가
• 2019년 Yang Song의 논문 NCSN으로 부활했음