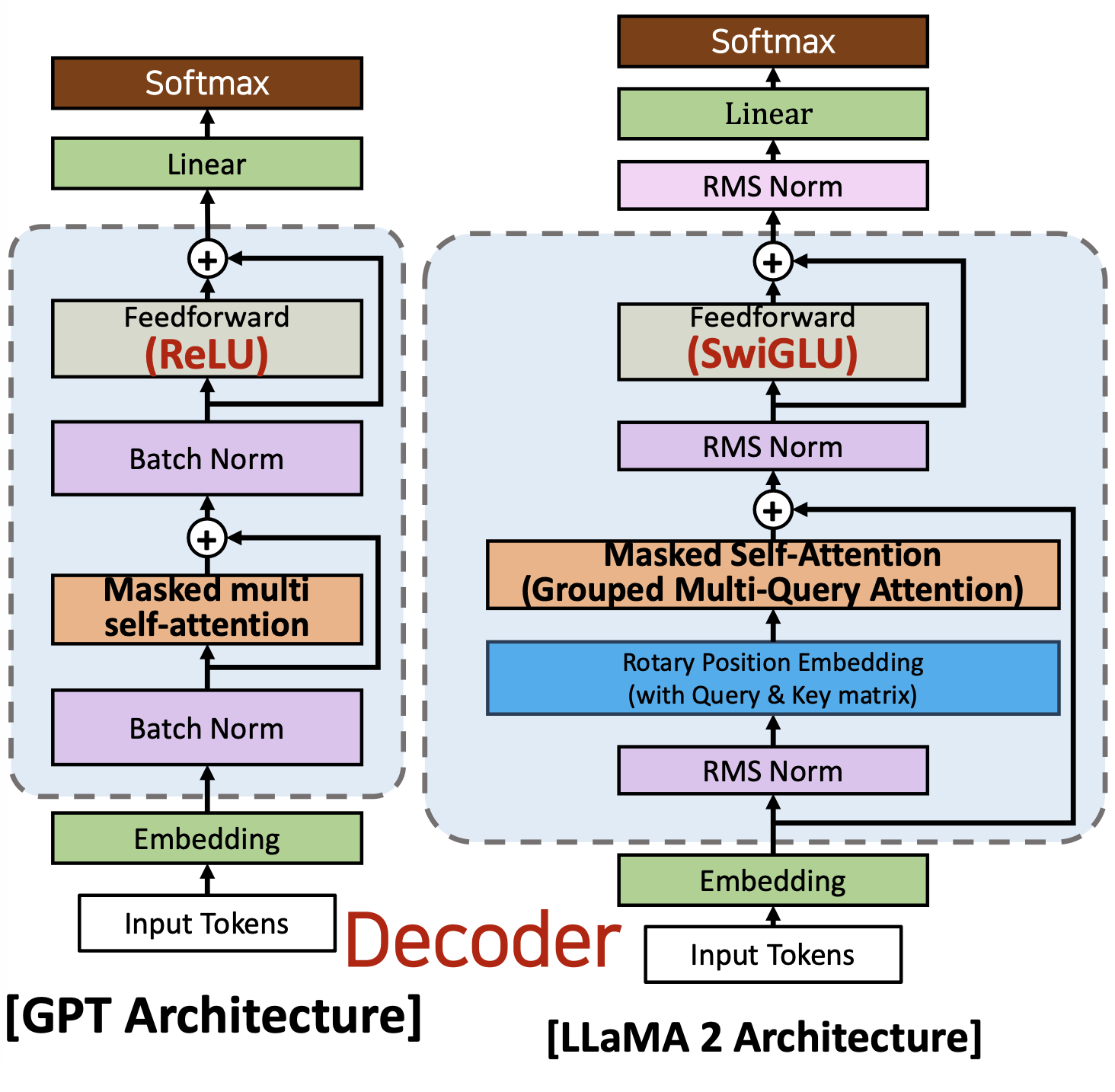
LLaMA 아키텍쳐
- 기본적으로 META에서 2023년 2월에 개발한 LlaMA의 아키텍처는 GPT와 거의 같다
- 그러나 LlaMA 아키텍처와 GPT 아키텍처 간에는 몇 가지 차이점이 있다.
구성
- RMS(Root Mean Square) Normalization
- LlaMA 2는 배치 정규화를 사용하는 대신 RMS 정규화를 사용합니다
- SwiGLU Activation Function
- ReLU 함수을 사용하는 대신 LlaMA 2는 SwiGLU 함수를 사용합니다
- Rotary Embeddings(회전식 임베딩)
- LlaMA 2는 포지셔널 임베딩(임베딩 레이어 안의)을 사용하는 대신 로터리 포지셔널 임베딩(RoPE, 디코더 블록에서)을 사용합니다
- Grouped Query Attention(그룹화된 쿼리 주의)
- Multi Head Attention을 사용하는 대신 LLAMA 2는 Grouped Query Attention을 사용합니다
- Multi Head Attention을 사용하는 대신 LLAMA 2는 Grouped Query Attention을 사용합니다
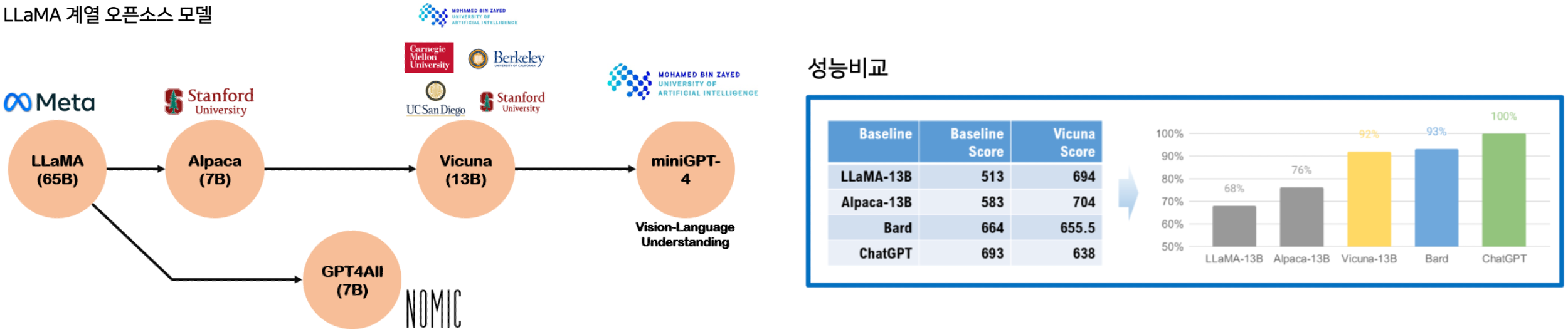
LLaMA vs Alpaca vs Vicuna
Alpaca (알파카)
- 알파카 : LLaMA-7B 기반으로 Fine Tuning한 모델 (스탠퍼드대 에서 개발자들을 위해서 개발. 5만 2천개 데이터로 챗GPT와 비슷한 성능. 저렴한 학습비용 $600이하. 2023년 3월 발표)
Vicuna (비쿠나)
- 비쿠나 : LLaMA-7B 기반으로 Fine Tuning한 모델 (UC Berkeley, 스탠퍼드, UCSD, 카네기멜론대, MBZUAI에서 개발자들을 위해서 개발.) 그러나 라마와는 다르게 Encoder-Decoder 모델이고 텍 스트 분석 및 생성에 중점을 둔 LLaMA와는 다르게 대화형에 중 점을 둠. ChatGPT에서 생성한 인간-ChatGPT 대화 7만 개로만 학습해서 챗GPT 성능 90%나 달성하고 LLaMA 보다 훨씬 뛰어 난 성능 (그러나 LLaMA-Chat 버전도 뛰어남). 2023년 4월 발표
Batch Normalization
- 학습과정에서 배치당 평균과 분산을 이용하여 데이터의 분포를 정규화하는 과정
- 학습 파라미터를 조정함으로써 Batch Normalization(배치 정규화)는 데이터가 목표 평균(target mean) 및 표준 편차(standart deviation)를 갖도록 보장합니다
- GPT 에서 사용
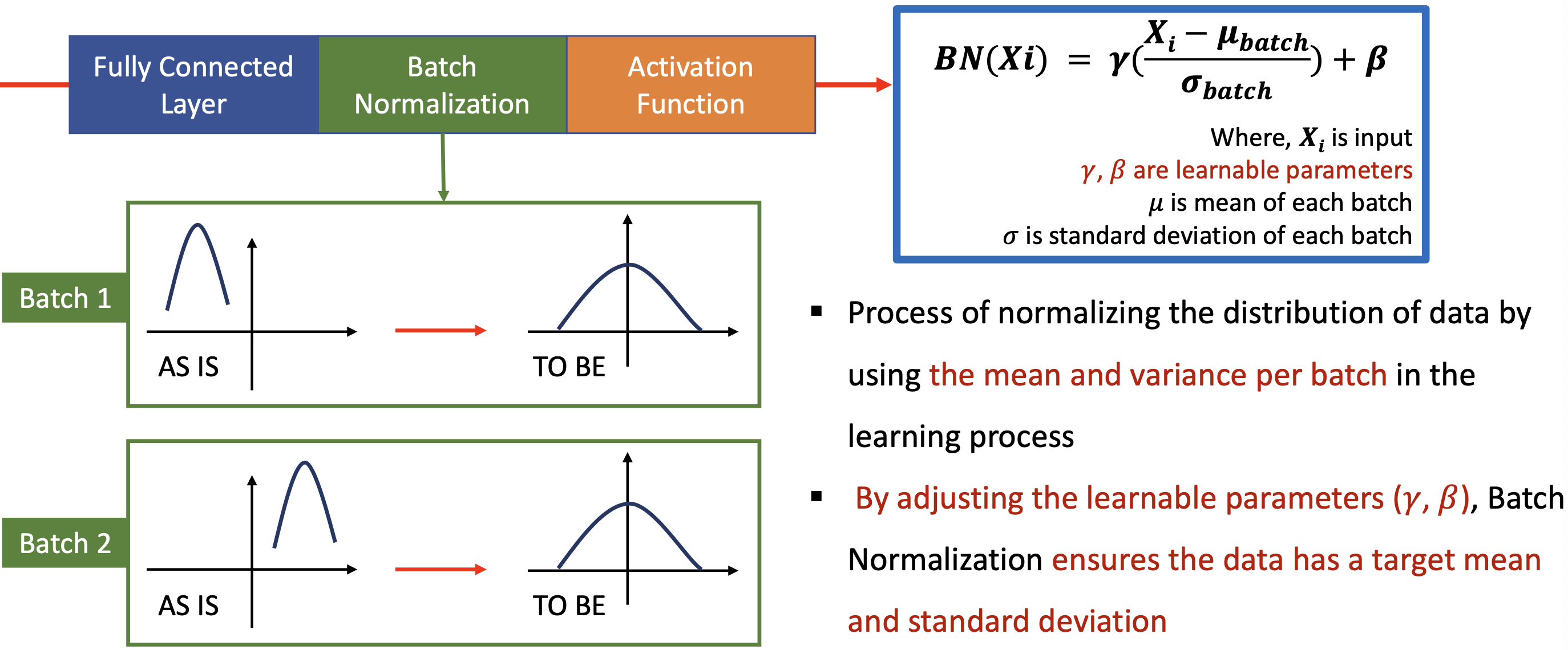
배치 1의 경우 데이터들이 왼쪽에 쏠려있고, 배치 2의 경우 데이터들이 오른쪽에 쏠려 있는 등 들쭉날쭉하다
이러다보면 나중에 학습할 때 그레디언트가 급격하게 움직이면서 잘 안된다
그래서 정규화를 시켜서 같은 mu 로 끌어오는 방법인데
감마와 베타를 사용하여 전체 배치들이 중심인 전체 평균으로 끌어올 수 있도록 한다.
RMS Normalization
- RMS 정규화는 layer 내의 평균 제곱근(root mean square)을 계산하고 이 값을 사용하여 정규화한다.
- RMS 정규화에는 배치 정규화와 같은 학습 가능한 파라미터가 없다.

왜 LLaMA 는 RMS 정규화를 적용하는가
- 계산 효율성
- RMS 정규화에서는 입력의 합의 제곱근(square root of the sum of the input)만 계산하면 되지만, 배치 정규화에서는 입력의 평균과 분산(mean and variance of the input)을 계산해야 한다.
- RMS 정규화는 배치 정규화보다 훨씬 빠르고 계산 비용이 적게 든다.
- 안정성
- 배치 정규화(Batch Normalization)는 매우 크거나 매우 작은 숫자를 다룰 때 수치 불안정으로 인해 어려움을 겪을 수 있습니다
- 그래서 감마와 베타의 파라미터를 도입한 것이다
- RMS Normalization은 이 문제를 덜 발생시킵니다
- RMS 는 투트를 씌우고 n으로 나눠주고 그것을 실제 입력 값에다가도 나눠주기 떄문에 안정적이다
- 배치 정규화(Batch Normalization)는 매우 크거나 매우 작은 숫자를 다룰 때 수치 불안정으로 인해 어려움을 겪을 수 있습니다
- 비선형성
- RMS 정규화는 모델에 비선형성을 제공하여 데이터에서 더 복잡한 패턴을 포착할 수 있습니다
- 배치 정규화는 이러한 패턴을 효과적으로 포착하지 못할 수 있는 선형 변환입니다
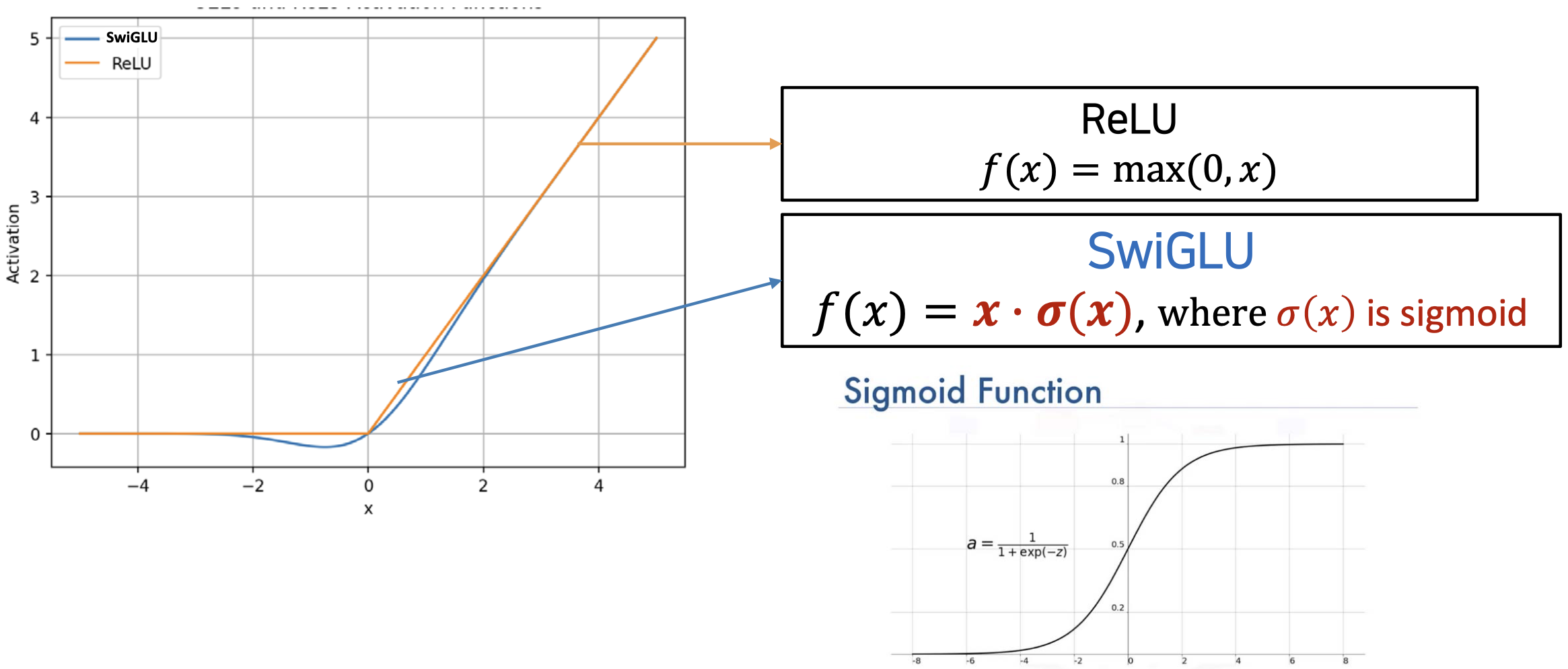
SwiGLU and ReLU
- ReLU는 단순하고 계산 효율적이지만 음수 인풋을 취하지 않는다 (최소가 0이다)
- SwiGLU는 시그모이드 컴포넌트를 사용하여 음수 입력에 대해 원활한 transition을 제공한다.
- 그러나, SwiGLU는 ReLU에 비해 시그모이드 컴포넌트로 인해 계산적으로 더 비싸다.
- 활성화 함수을 SwiGLU로 변경하여 LlaMA의 성능을 향상시킬 수 있었다.
활성함수를 사용하는 이유?
LLM 도 딥러닝을 사용하는데, 경사하강법에 의해서 계속 활성함수를 사용하다보면 기울기가 0에 가까워지는데, 이를 방지하기 위해 라마에서는 SwiGLU 를 사용
수식
- SwiGLU : 인풋에다가 시그모이드를 곱해줌
- (-) 값을 잃어버리는 단점을 해결한다.
- non linear 의 장점도 있다 (좀 더 많은 패턴을 반영할 수 있다)
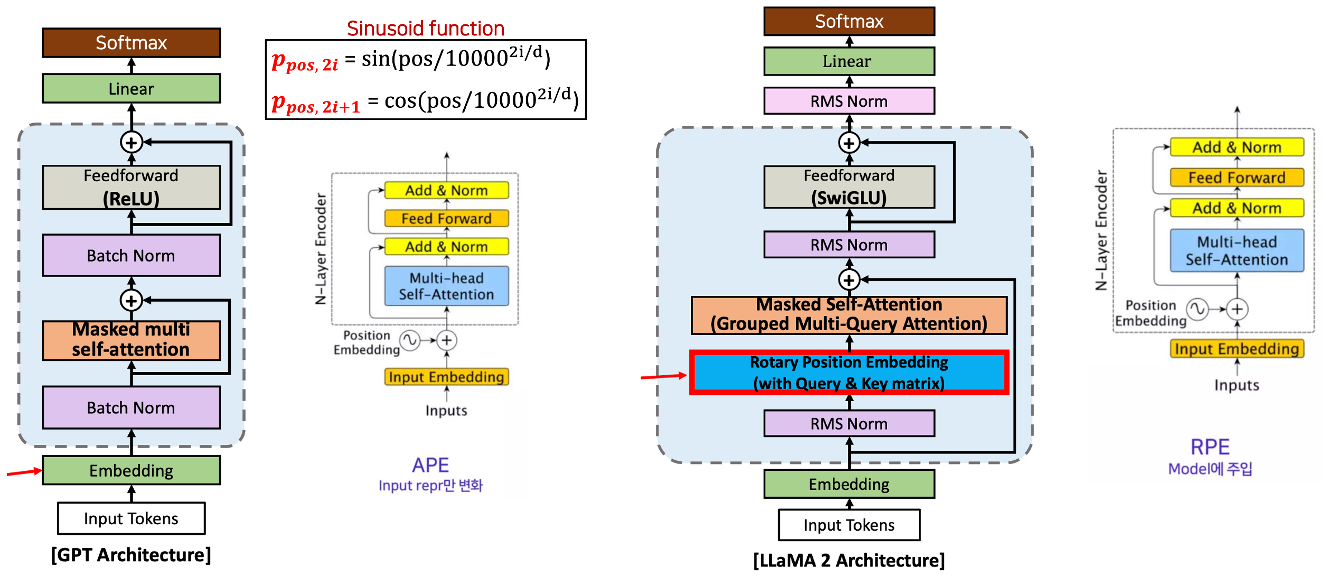
두가지 종류의 포지서녈 임베딩
- Absolute Position Embedding : BERT and GPT 에서 사용
- 각 토큰에 positional vector p 추가 (Sinusoid 함수. Absolute Positional Embedding)
- 일반적으로, positional vector는 임베딩 레이어에서 입력 토큰에 대한 Word Embedding 결과에 더해진다.
- Absolute Position Embedding: 최초 Input Token에 Position Information을 한번 주입해주고 끝냄 (어텐션 레이어에 들어가기 전에 절대 임베딩을 처음에 한번만 삽입)
- Relative Position Embedding : LLaMA 에서 사용
- Absolute Position Embedding 처럼 절대 위치가 아닌 위치 m과 n 사이의 상대적 거리 사용
- Query 와 Key가 Attention Layer에서 수행할 때 상대적인 위치 정보를 반영 (어텐션 레이어 안에 들어가서 해준다 - 아주 다른점)
- 어텐션 레이어 안에서 해주기 때문에 어텐션이 예를 들면 라마가 레어가 여러개가 있다면, 각 레이어마다 매번 상대 위치 임베딩을 한다는 것
- 즉, 매 Layer 마다 매번 Position Information을 Attention 수식 (모델 수식에 직 접 Multiplication)에 주입 (매 Layer 모델 마다 주입)
Review of Linear Algebra
- Definition of Orthogonal Vector
- length = 1 (단위벡터) 라면, “the ortho-normal vector” 라 부른다.
- 두 벡터의 각도 라면, 두 벡터는 orthogonal 이다.
- 두 벡터의 inner product 는 0일 것이다. (두 백터가 독립적이다. 닮은 꼴이 아니다. 만약 1 이면 직교가 아니고 서로 닮은 꼴이다).
- Orthogonal Vectors 의 성질
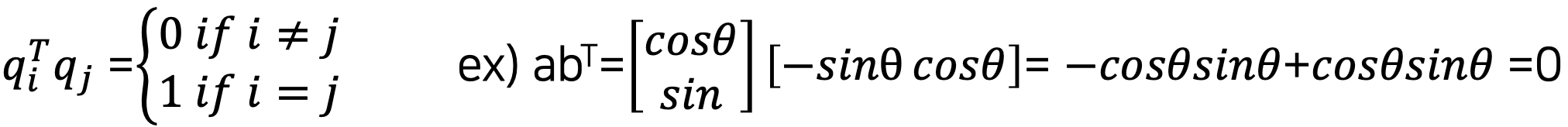
- Q가 square 라면, 이고
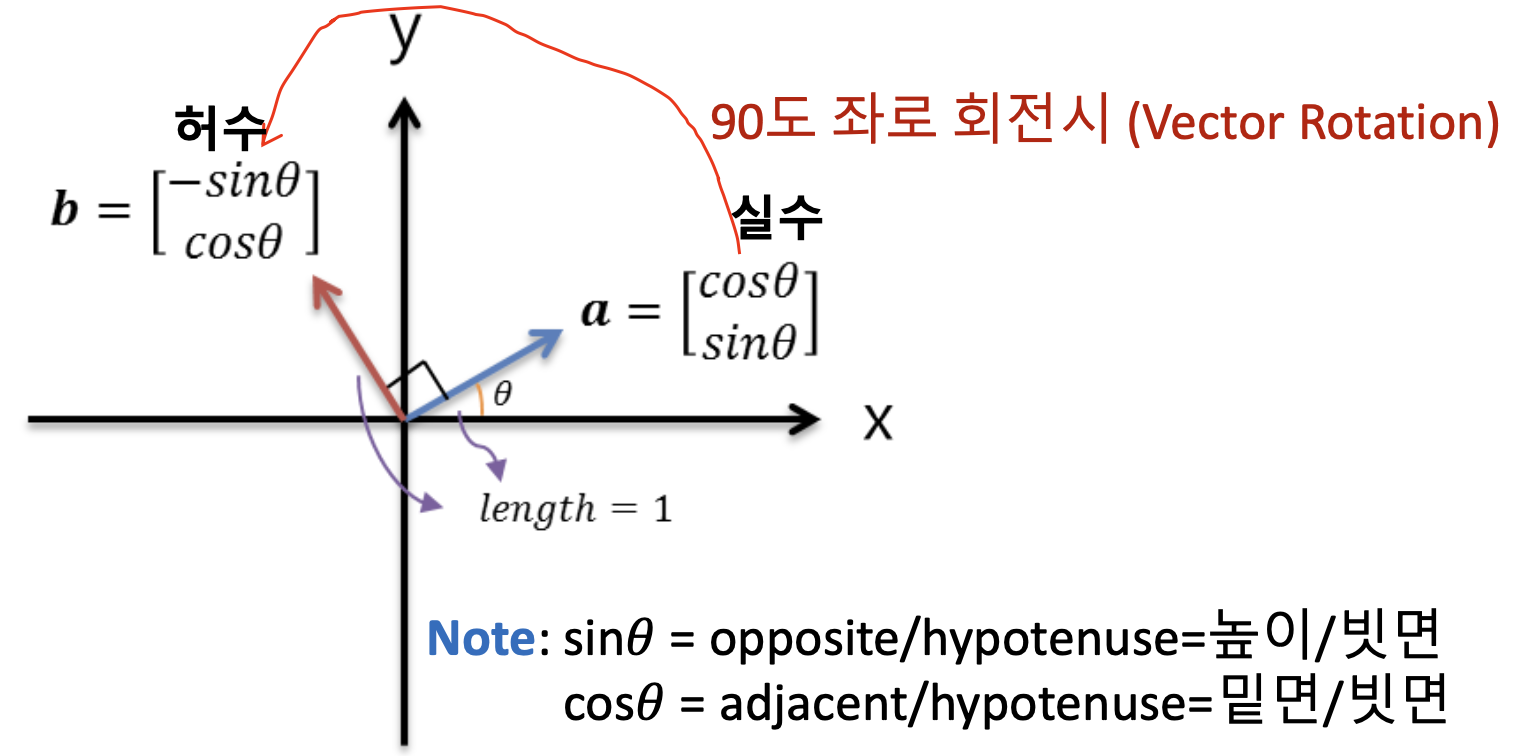
Rotary Positional Embedding (RoPE)
- 오소고널 벡터 개념을 활용한 것이 Rotation Matrix 이다.
- 는 차원 는 각도, 은 인덱스
- 위치 정보를 포함하도록 두 차원 각각에 대해 일정 각도만큼 회전
- 값은 transformer의
sinusoid와 같은 매핑 함수를 사용합니다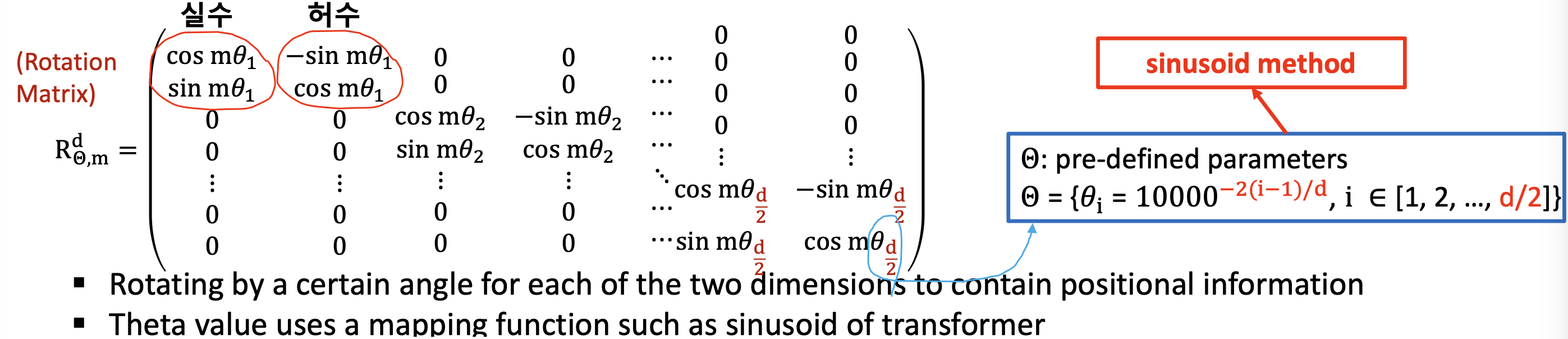
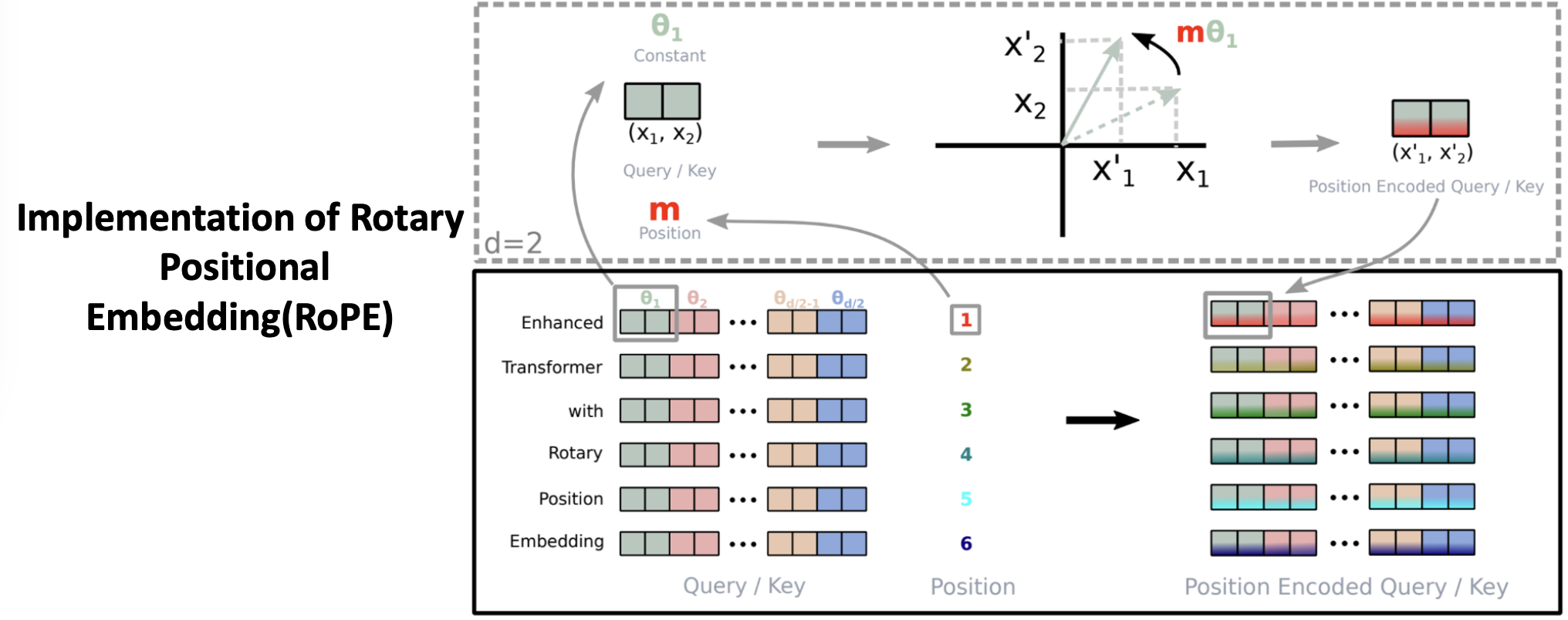
- 첫번째 Enhanced 토큰에 대해서 Rotary로 바꿔라 그러면은 m 인덱스를 곱해준다.
- 여기서는 실수와 허수 두개를 표시해주어 Rotaion Matrix 상에서 대각선으로 표시해준것이바로 Rotary Matrix 이다.
- 모델 차원의 뒷부분에 로 한 이유
- 실수파트, 허수파트가 있기 떄문에 로 나눠줌
- 로터리 포지션 임베딩은
sinusoid를 이용하여 구한 절대 포지션 값 값을 입력 (엄격하게 말하면 완벽한 90도가 아니라 절대 sinusoid 값) - 로터리 포지셔널 임베딩은 로테이션은 포함하되, 90도기 아니라는 것임
- 즉, 절대 sinusoid 위치 각도로 rotation 을 한다. 이게 다른 점!!!!!!!
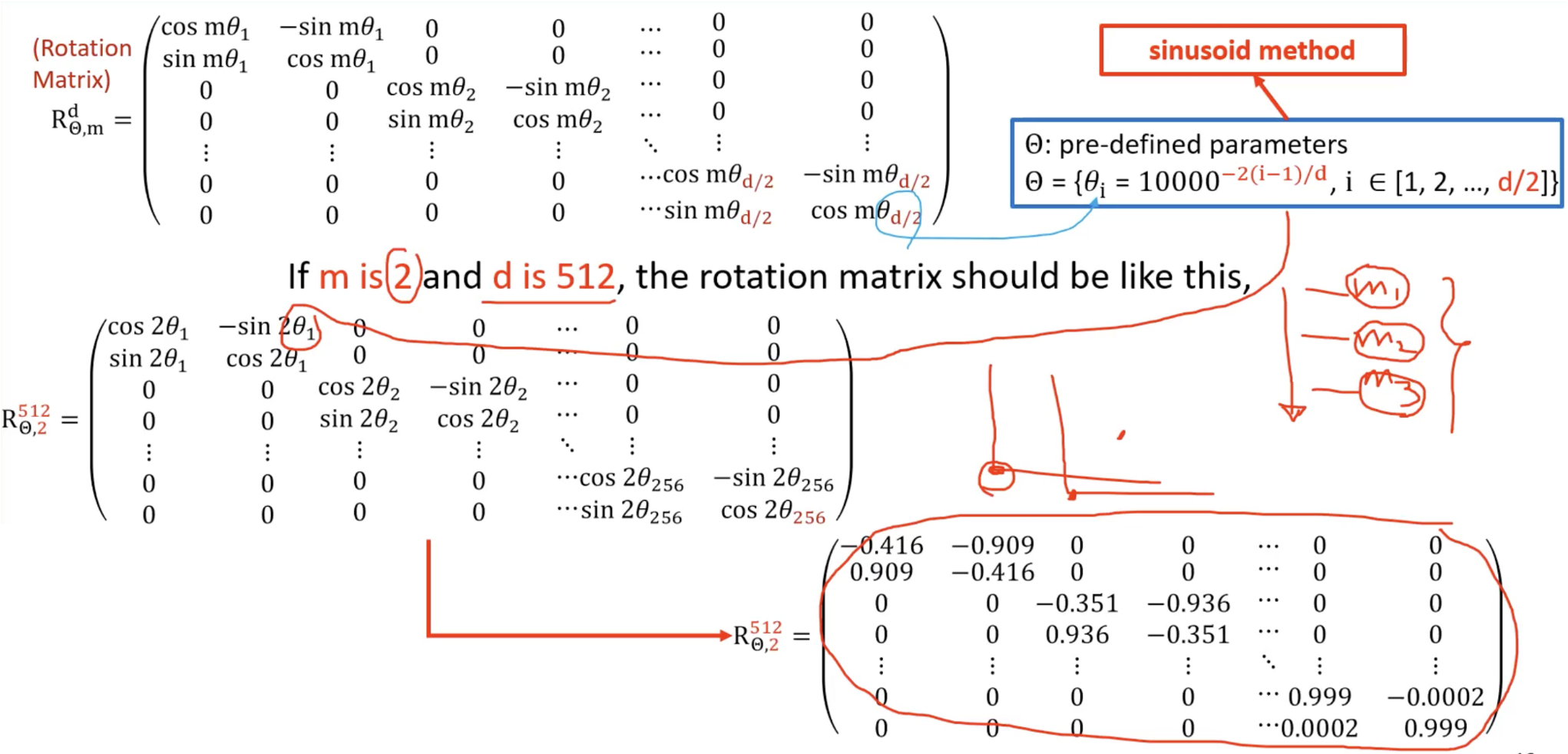
구체적인 숫자 계산
만약 위치 인덱스 이 2 이고 모델 차원 가 512 라면, sinusoid method에 입력을 하고 구해지는 절대 위치 각도를 값으로 사용한다. 계산된 Rotation Matrix는 오른쪽 아래와 같다.
절차가 복잡하긴 하지만 컴퓨팅 계산 시간이 오래 걸리지 않는다. 그렇다면 왜 상대 위치를 사용했을까?
의 절대적인 관계가 아닌 상대적인 관계 (다른 토큰과 내 토큰간의 차이) 를 반영
어떤 위치가 변하더라도 절대적인 위치가 처음에 0부터 시작했고, 어쩌다 보니 조금 아래쪽으로 내려왔다고 가정. 나와 다른 토큰간의 유사성, 어텐션관계가 중요하지 절대적인 위치가 중요하지 않다.
RoPE
- RoPE는 Relative Position Embedding based method 이며, 가산법(Additive method)이 아니라 곱셈법(Multiplicative method) + sinusoid method(Absolute Position을 사전에 주입)이다.
- Attention Layer 에서 Query와 Key의 Inner product를 수행할 때, rotation matrix를 곱하여 위치 정보(postional information) 반영
- Query 와 Key 에 대해서만 Rotary Positional Embedding을 적용하는 것이다.
수식
- 상대 위치는 Muliplicative method
- Relative 위치를 아래의 식의 하늘색 부분처럼 곱해준다. 어디에? ( 와 인풋 에 대해서)
- 절대 포지셔널 임베딩은 그냥 인풋 토큰에다가 그냥 더해준것이다. (이전에 배운 내용)
- 하늘 색 rotation matrix 를 , 에 대해서 곱해주고 , 에 대해서 곱해준다. 그리고 나서 앞에 있는 것을 transpose 해준다.
- 이것을 정리하면 :
을 보면 알수있는 것은 서로 다른 토큰간의 상대적인 위치를 나타낸다고 알수있다.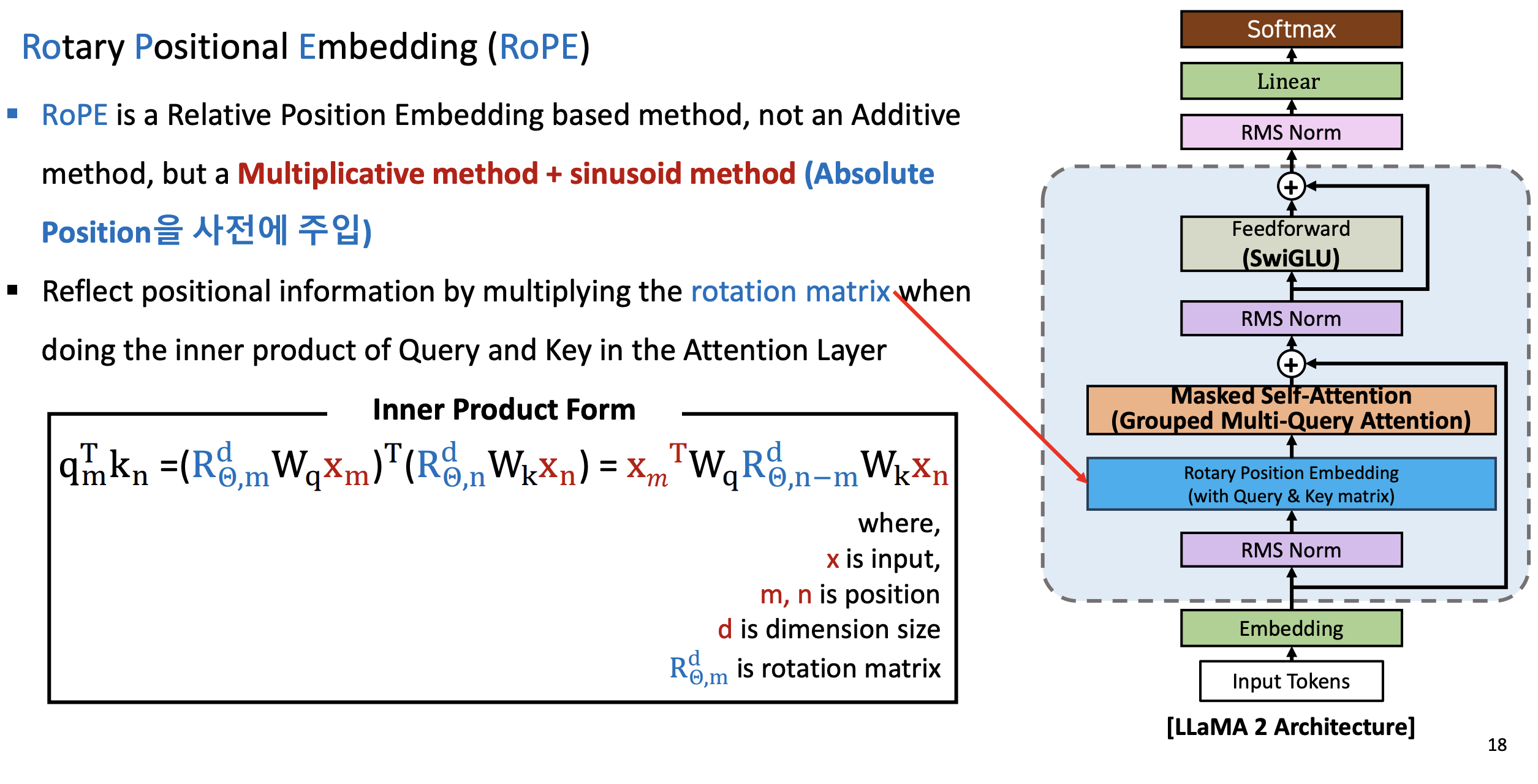
Grouped Query Attention (GQA)
- Multi-head Attention은 H(어텐션 헤드 개수)개의 QKV(Query, Key, Value)를 가진다.
- 8개의 각 헤드에 대해서 Q 에 대한 각 key 값 value 를 구해주고 각각 inner product 곱하고 곱하고 즉, 일대일로 대응 했었다.
- 각각의 KV 텐서를 로드하기 위해서는 많은 메모리가 필요하다.
- Multi-query Attention은 H개의 Q(Query)와 1개의 KV(Key, Value)를 가진다.
- 모든 헤드들의 개수에 대해서 하나만 수행하는 것.
- 모든 Q(Query)는 KV(Key, Value)를 공유한다.
- Multi-query Attention으로 메모리를 절약할 수 있다.
그러나 Multi-query Attention은 Multi-head Attention에 비해 모델의 성능을 저하시키고 모델의 학습을 불안정하게 만들 수 있다.
이 문제를 해결하기 위해 Grouped-query Attention(그룹 쿼리 주의) 소개 KV 헤드의 수를 H개에서 1개로 줄이는 대신 적절한 G 그룹으로 줄인다.
멀티 쿼리 어센션같이 KV 헤드들의 숫자(K와 V에 대응하는 헤드개수)를 하나로 줄이는 것 대신, G개 만큼의 그룹을 짜서 (예시처럼 꼭 2개를 묶으라는 법은 없음) 축소하는 것
- Grouped-query attention
- 하나의 key로 계산, 하나의 value로 계산하여 컴퓨팅 타임을 줄이는 대안
- Grouped query attetion 그림에서 보면 멀티 헤드 어텐션 부분에서 2개의 key가 아닌 하나의 key 사용
- 각 Qeury에 대해서 Value도 마찬가지로 두 개 중 하나만 계산
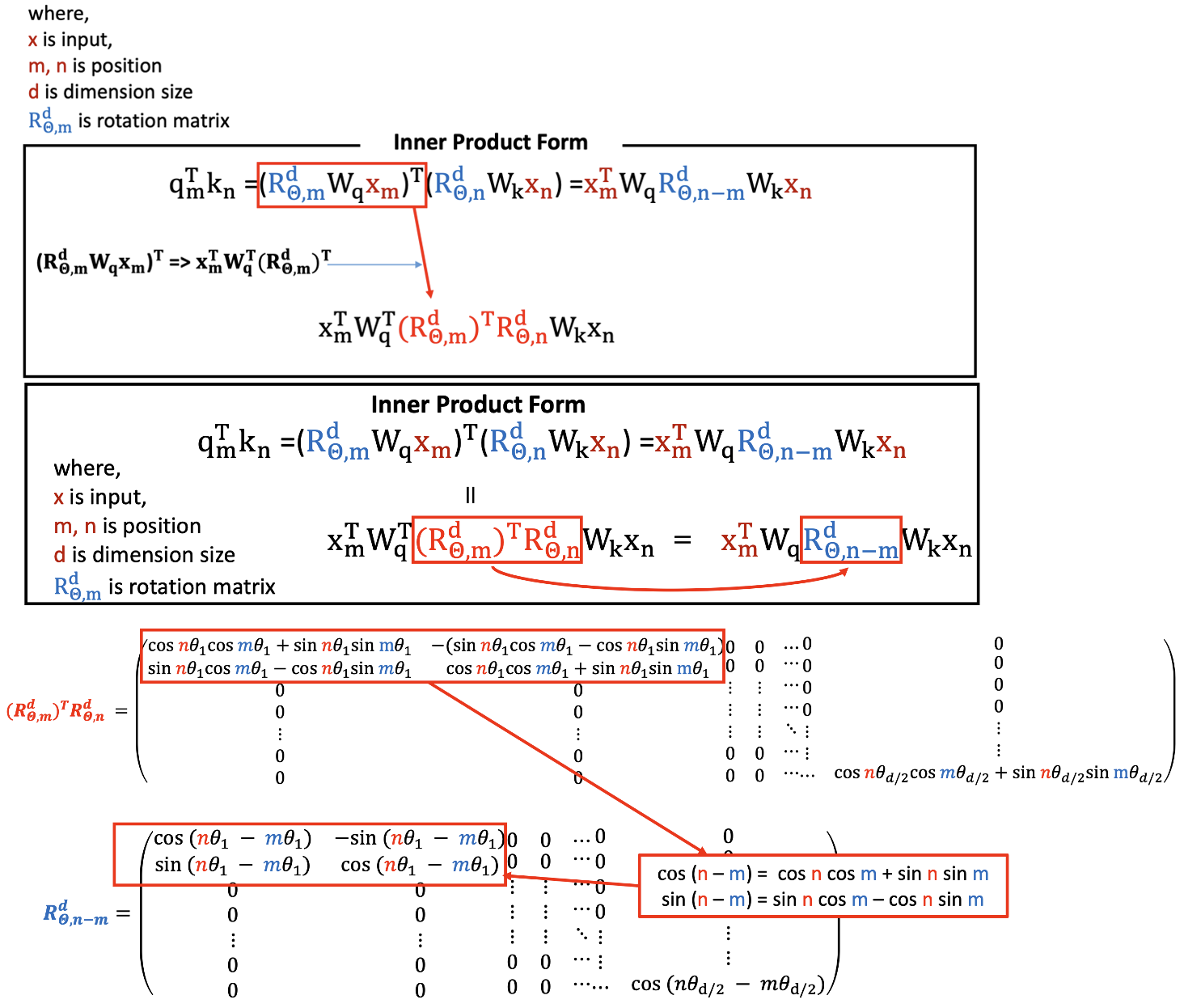
샘플당 컴퓨팅 비교
- 보통 "G"는 H의 제곱근으로 설정됩니다:
# of groups = HH- 해드가 H 가 예를들면 4개면은 루트를 씌워서 그룹은 2개를 하라고 제안함
- GQA는 Multi-query Attention 만큼 빠르며 성능은 Multi-head Attention과 비슷하다.
- GQA, MHA, MQA 비교
- 그룹의 개수를 증가시키면서 시가닝 점점 올라가면서 64개 올리니까 확 올라감
- 적절한 개수는 몇개일까? (2~4 일듯하다)
- 모든 각각의 MHA 는 가장 많은 시간이 소요됨
- Inference : 새로운 입력 데이터를 모델에 적용하여 결과를 산출합니다(모델 테스트와 같이)
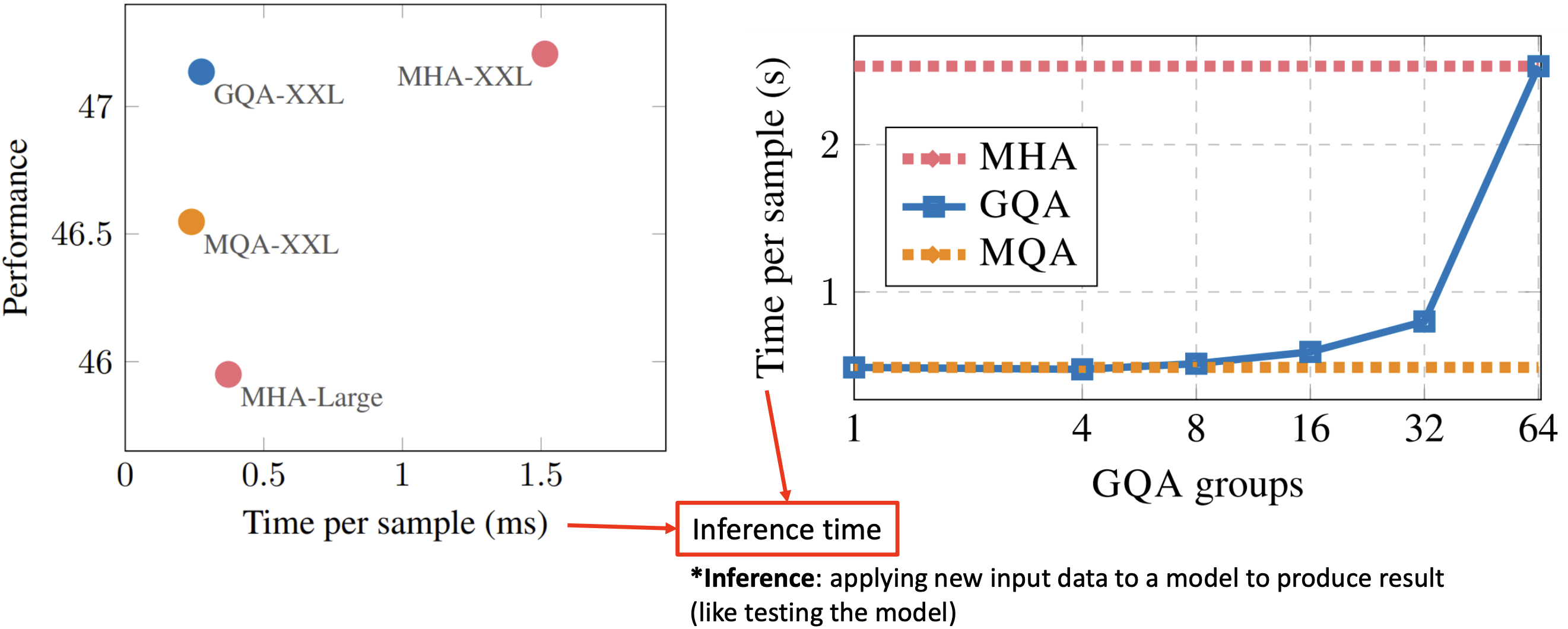
LLaMA 2 아키텍처
# student 라는 output 을 예측
I am a student- LLaMA 2 는 decoder-based 모델이다
- 모델은 오직 한번에 하나의 토큰만 생성한다.
- 현재 레이어의 아웃풋은 다음 레이어의 인풋 토큰이 된다 (Autoregressive라고 한다 - RNN과 비슷)
- 마지막에는 마지막이다 라고 표시
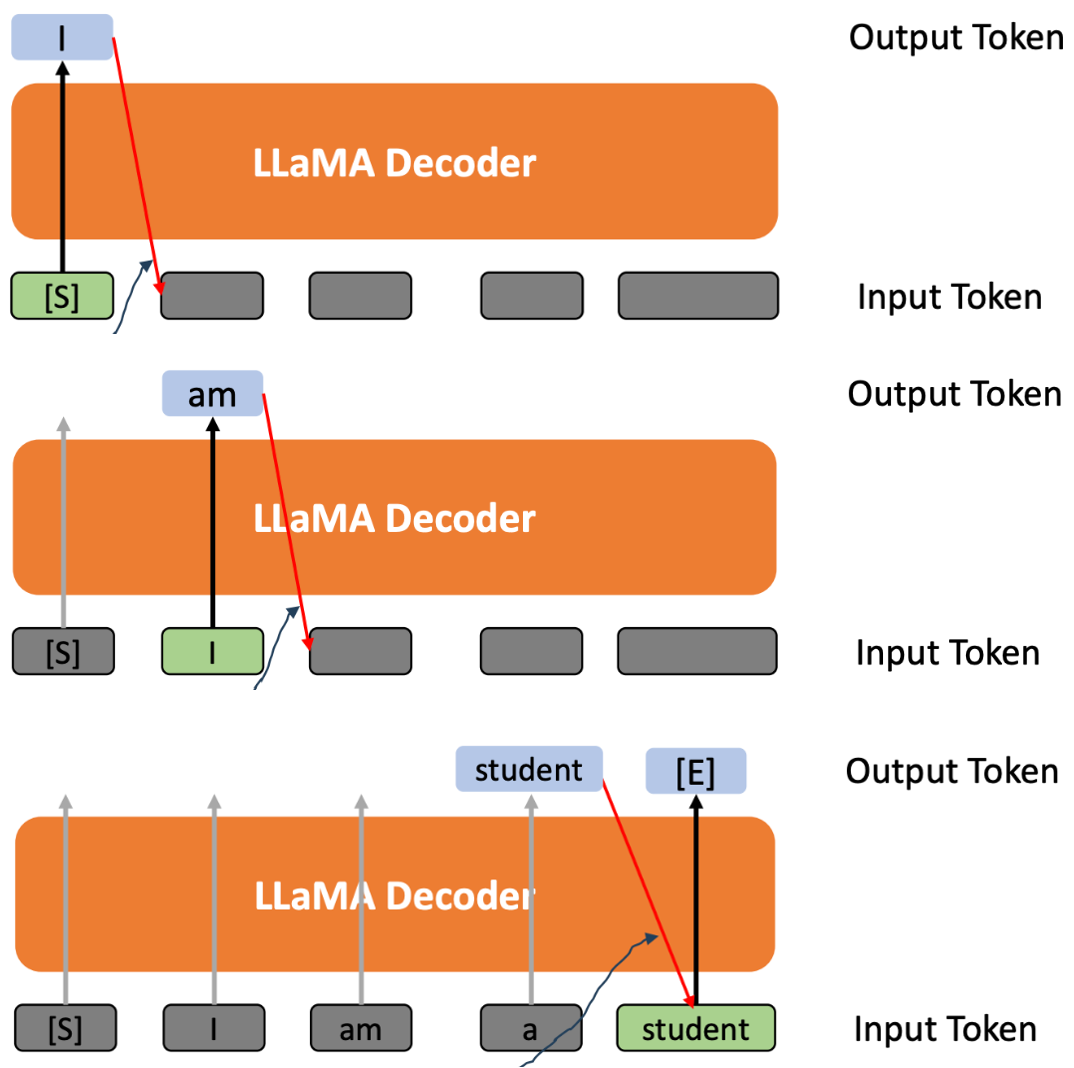
Numerical Example
Input Token Size and d_model
- 라마 2 의 dictionary 는 약 3,2000 개정도 된다
- 그다음에 모델의 차원은 (헤드를 32개까지 사용할 수 있다 - 굉장한 다양성 부여)
- 모델의 차원과 마찬가지로 인풋 사이즈는 최대 4096개 까지 가질 수 있다. (라마 1 에서는 2048 개 였다)
(1) Embedding
- 단어를 토큰화 tokenization
(2) 첫 번째 RMS Norm
- RMS 정규화를 하고 나면은 Input token size 와 의 곱으로 이루어진 Output 이 나온다
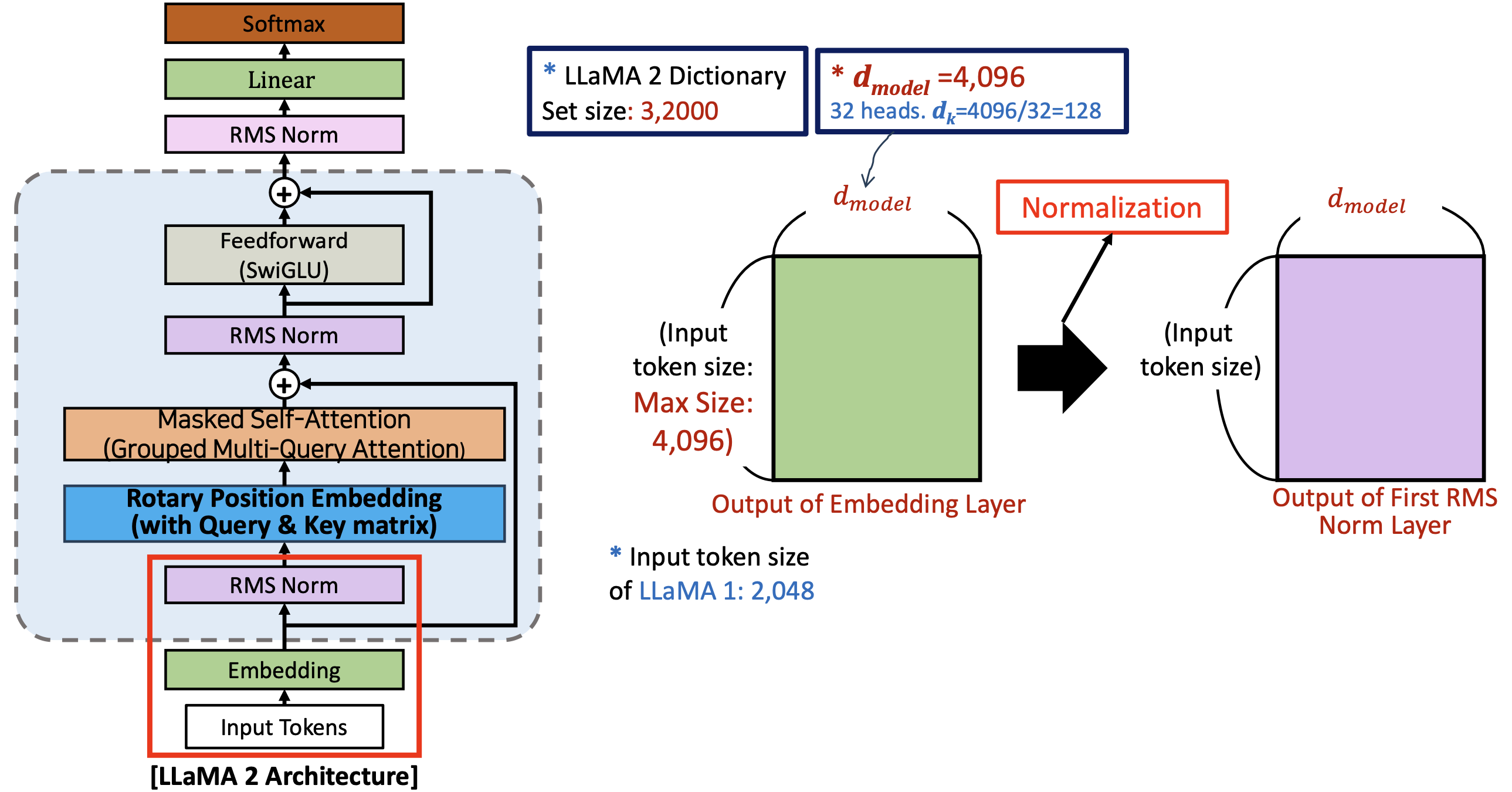
(3) Rotary Position Embedding
- 기존 GPT 와 BERT 와 다른점을 유심히 보기. 상대 위치를 구할 떄는 인풋 matrix 에 곱해준다고 했다
- Rotation matrix 의 차원은
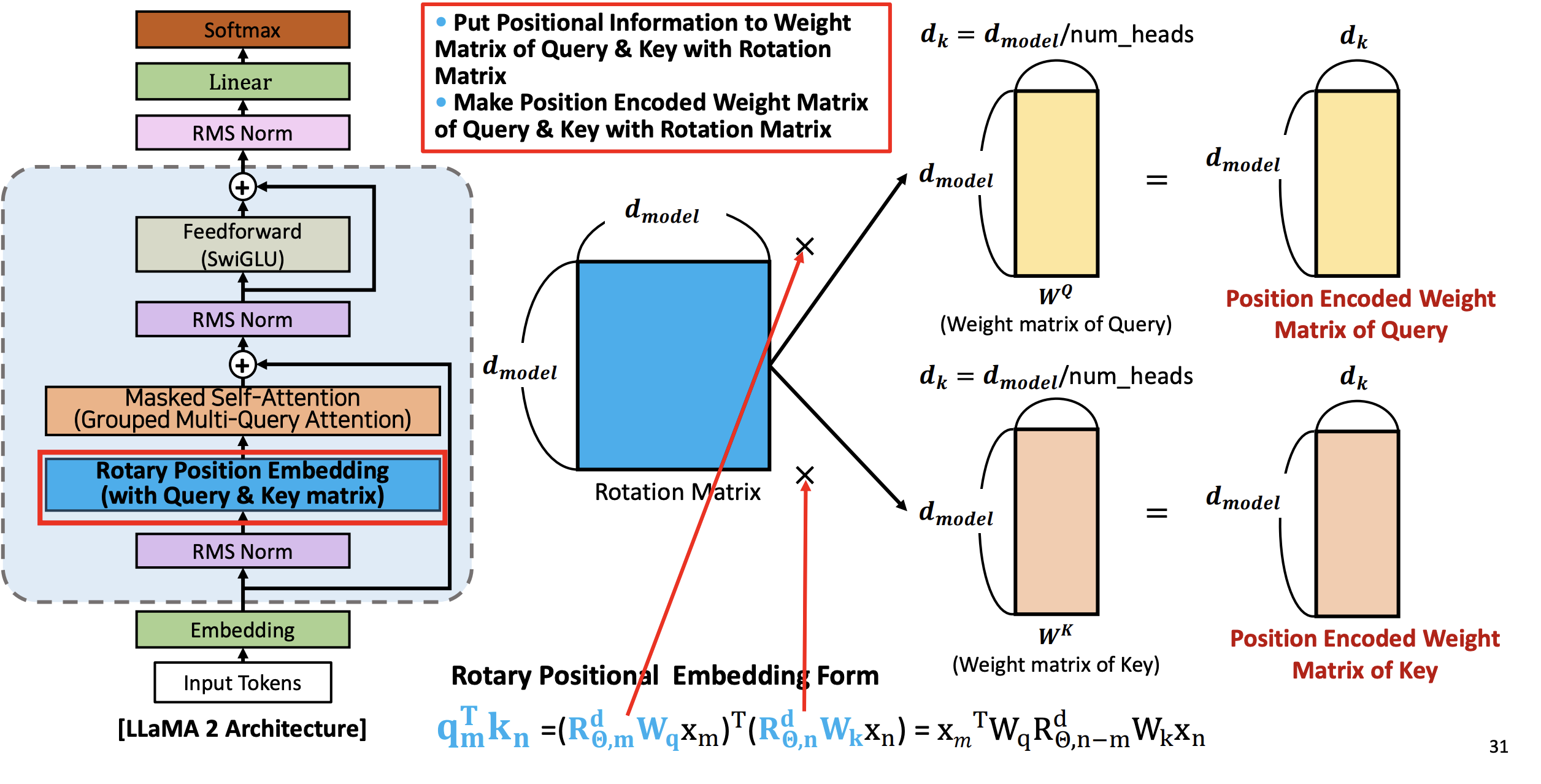
attentio score (로테이션을 곱한)
Rotation Matrix 에 쿼리의 Weight Matrix 에 곱해주고 그 다음에 Key 의 Weight matrix 에 좁해줌
그렇게 곱한 뒤 Postional Encoded Weight Matrix of Query 와 Position Encoded Weight Matrix of Key 가 만들어진다.
(4) Grouped Multi-Query Attention(Masked Self-Attention)
-
수식에서 하늘색 부분, 각 R 과 W 는 곱해서 Postional Encoded Weight Matrix of Query 와 Position Encoded Weight Matrix of Key 를 구했다. 아래 그림상에서 이제 인풋 x, x 만 곱해주면 된다
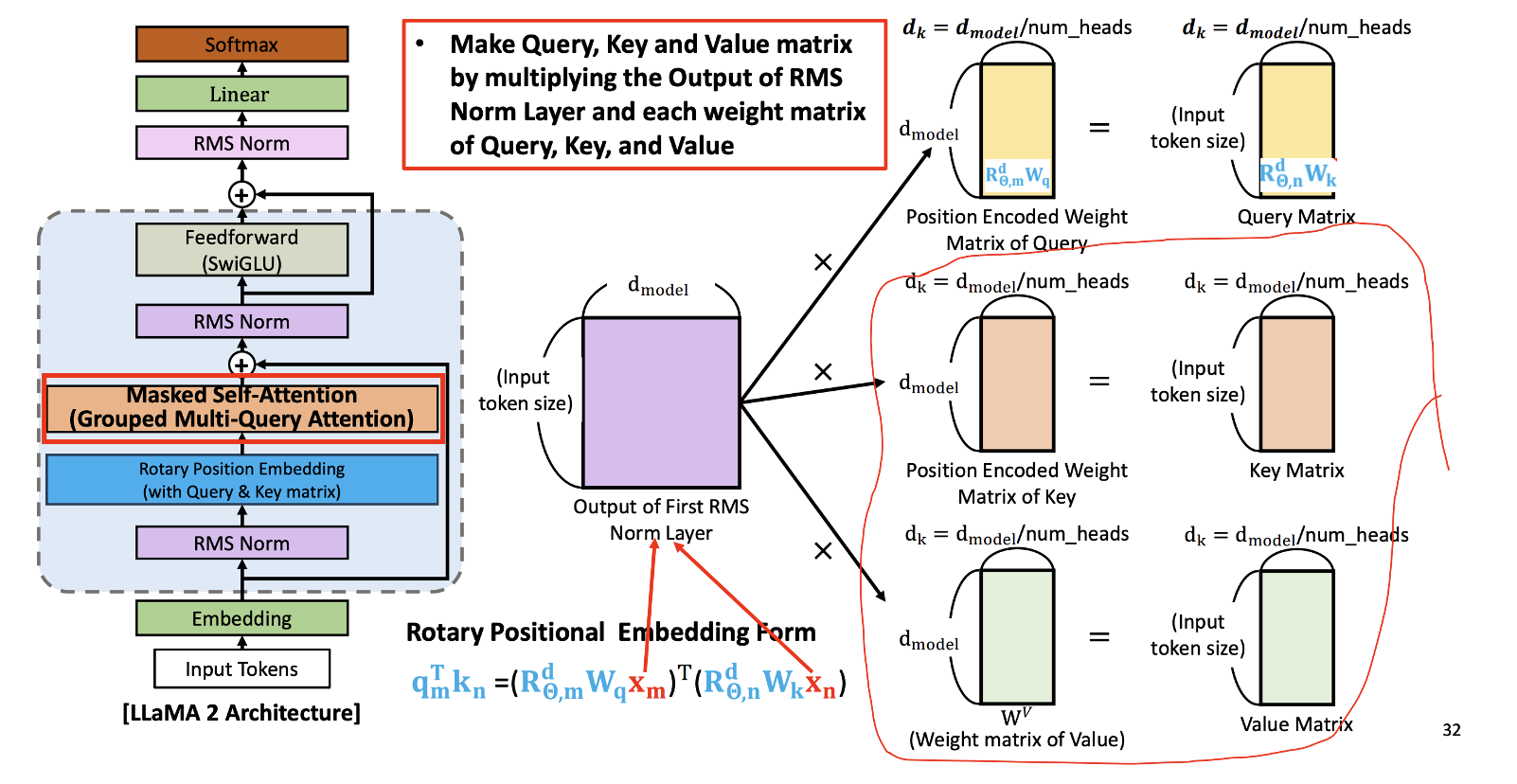
Value도 마찬가지로 Weight matrix 를 계산한 이유? 뒷장에서 나옴
-
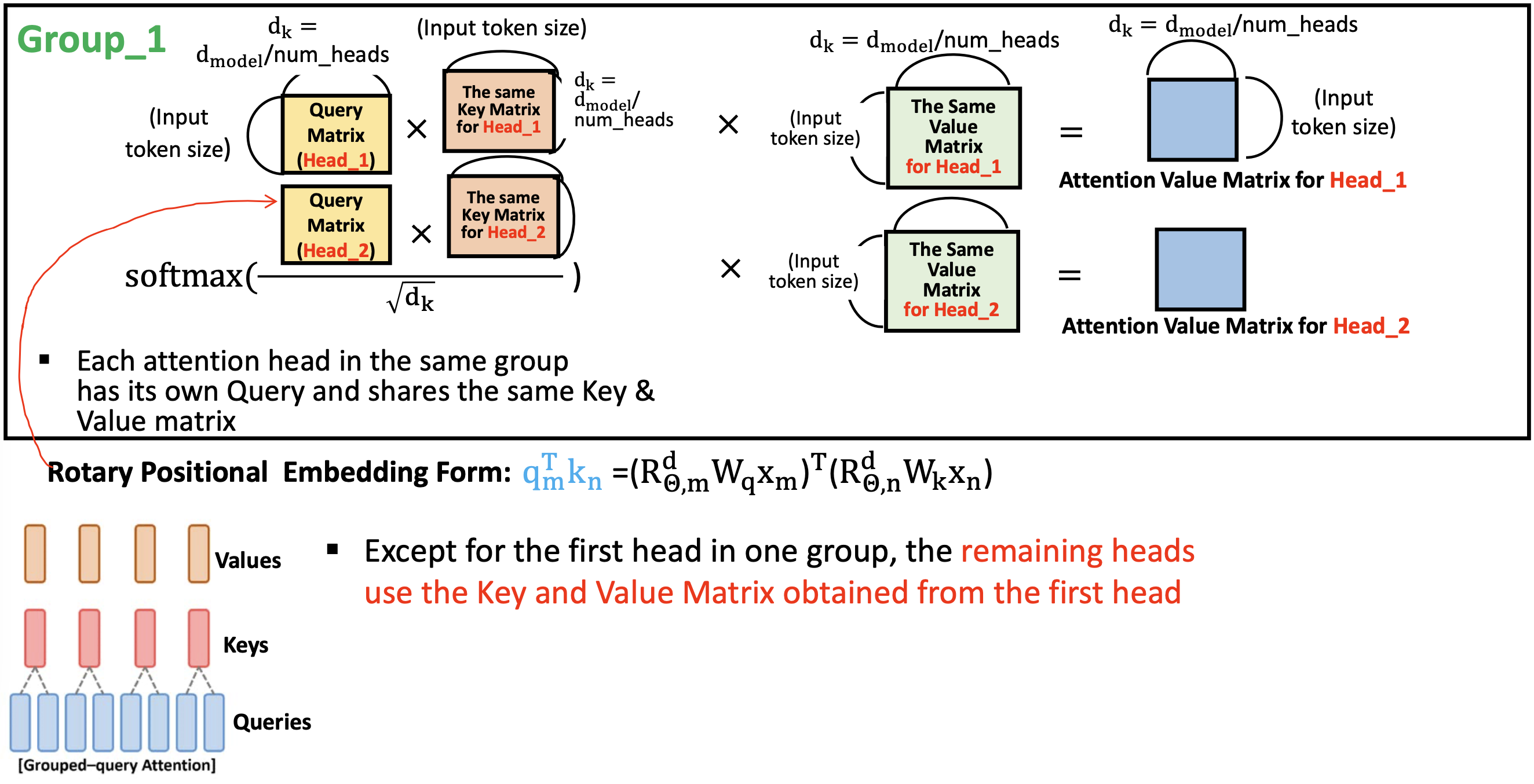
Grouped Multi-Query Attention 과정
- 어텐션을 구해야 하는데, 우리가 Grouped Multi-Query Attention을 사용한다고 했었다
- Head_1과 Head_2를 하나의 그룹으로 봤을 때, 거기에 곱해주는 뒤의 Key matrix 는 하나만 곱해진다고 했었다.
- 첫 번쨰 Head_1 에서 Key Matrix 계산 (Head_2도 동일한 key matrix 사용)
- 스케일 다운 후 소프트 맥스 적용
- 첫 번째 Head_1 에서 Value Matrix 계산 후 마찬가지로 Head_2 에서도 동일한 값 Value Matrix 값을 사용하여 attention score에 곱한다.
- 최종적으로 각 헤드마다 attention value matrix 가 나온다.
(5) Concatenated Heads Matrix
- 어텐션 레이어를 통해 계산된 각 헤드의 attention value matrix를 concatenate
- 그런 다음 concatenated matrix에 weight matrix 를 한번 더 곱하기
- 그 Weight matrix 값은 d_model x d_model
- 헤드들이 다 합해진것이기 때문에 사이즈가 d_k 가 아닌 d_model 이다.
- Output of Grouped-query attention (Attnetion layer) 도출
- (Input token size) x (d_model)
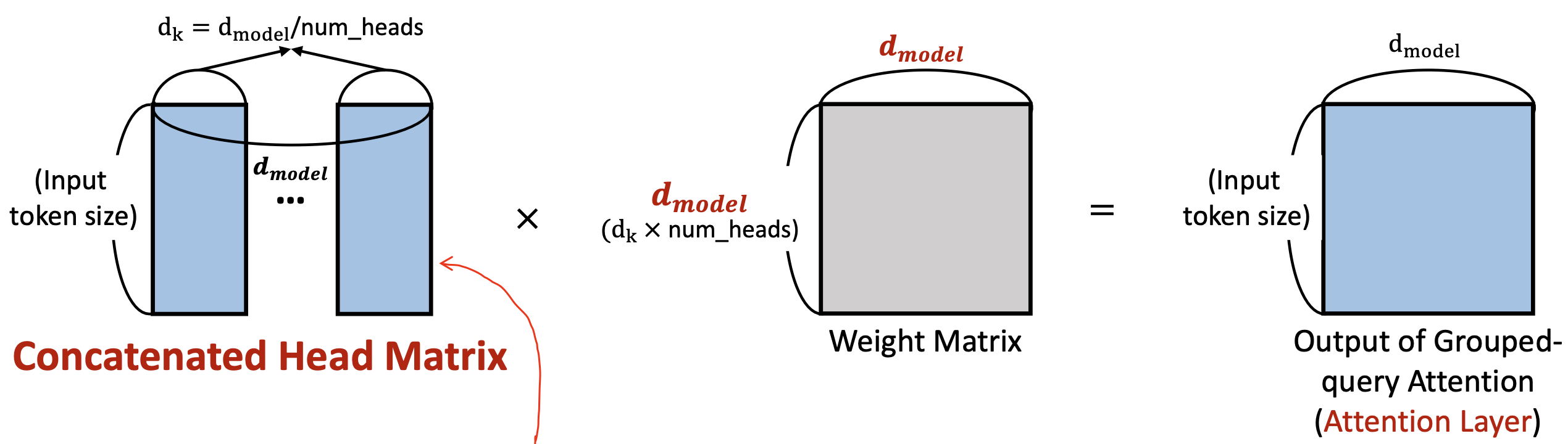
- (Input token size) x (d_model)
(6) 두 번째 RMS Norm
- RMS 를 하기 전에 방금전 group multiquery attnetion 으로 나온 Output of Grouped-query attention (Attnetion layer)에 초반 Embedding layer 의 Output을 더해준다.
- vanish problem 을 방지하기 위해서 하지 않았나 생각하신다함
- 이렇게 두개를 더한 다음 두번째 RMS Norm 으로 들어간다.
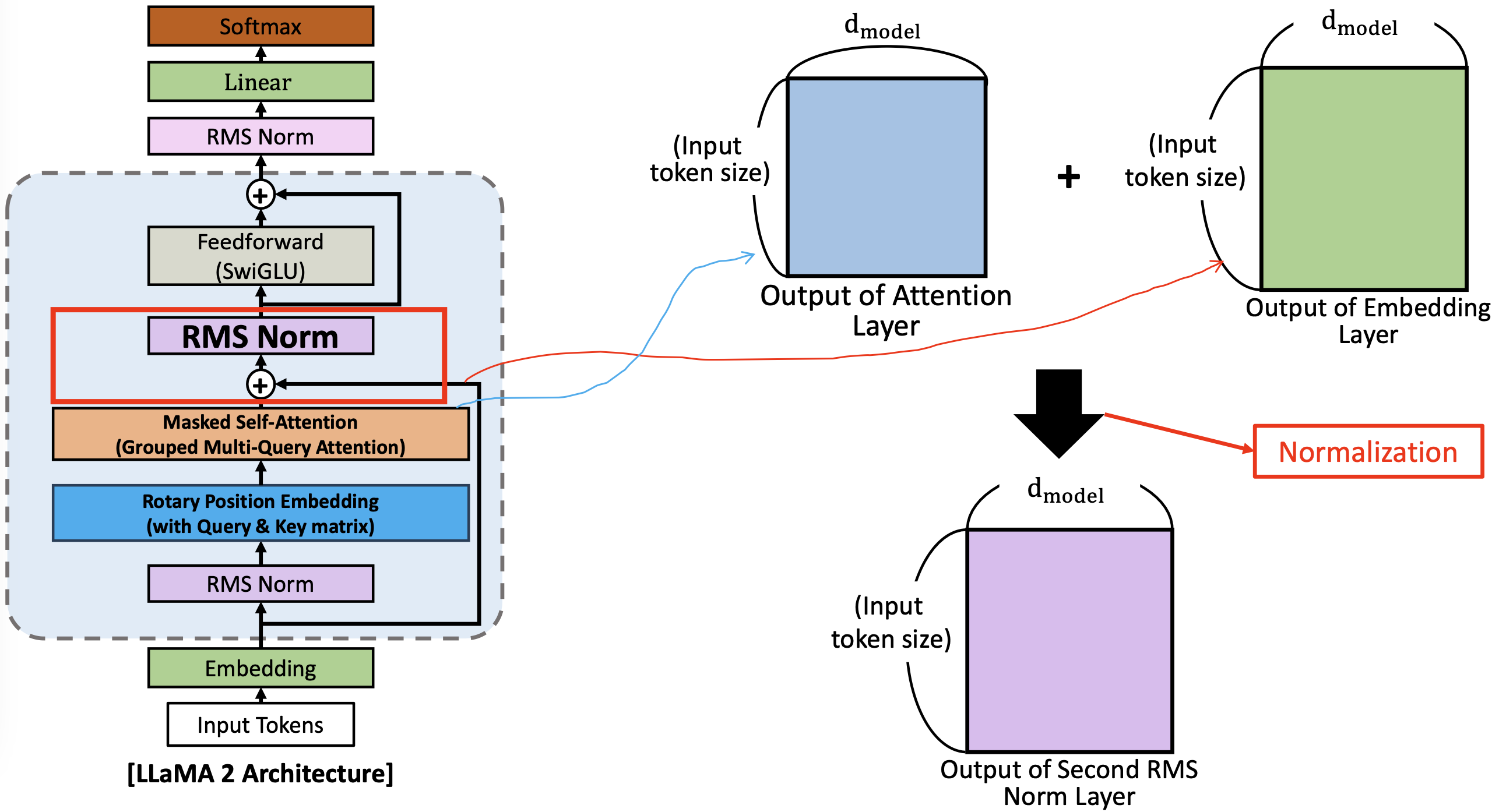
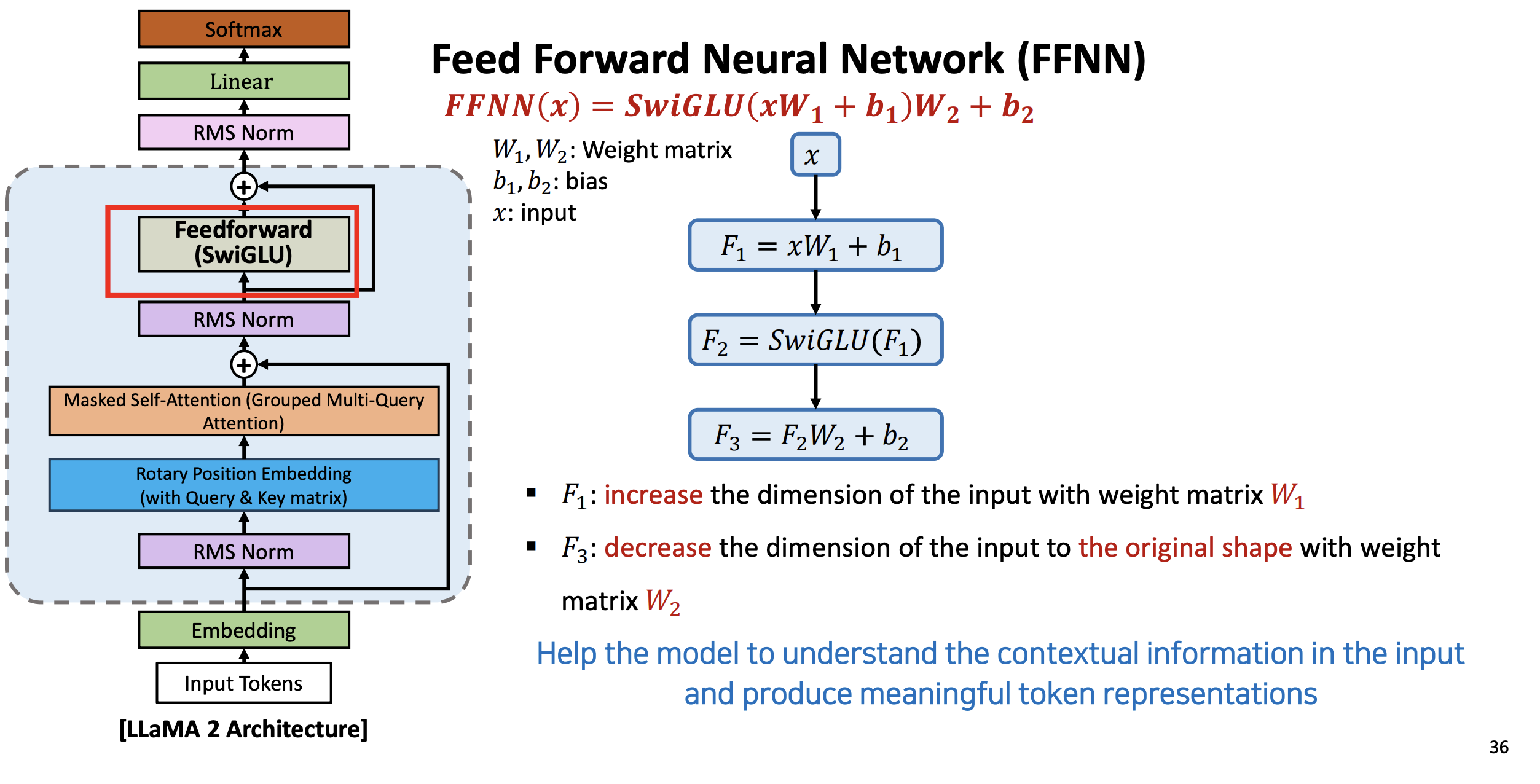
(7) SwiGLU FeedForward
- 두 번째 RMS 정규화 한 것을 가지고 다음 FFNN 에서 SwiGLU 라는 활성화 함수를 쓴다.
- F1 : 컴퓨팅 타임을 줄여주기 위해 가중치 행렬 을 사용하여 입력 차원을 늘린다.
- d_ffnn 은 사용자가 결정할 하이퍼 파라미터
- 모델이 입력의 상황 정보를 이해하고 의미 있는 토큰 표현을 생성할 수 있도록 돕는다.
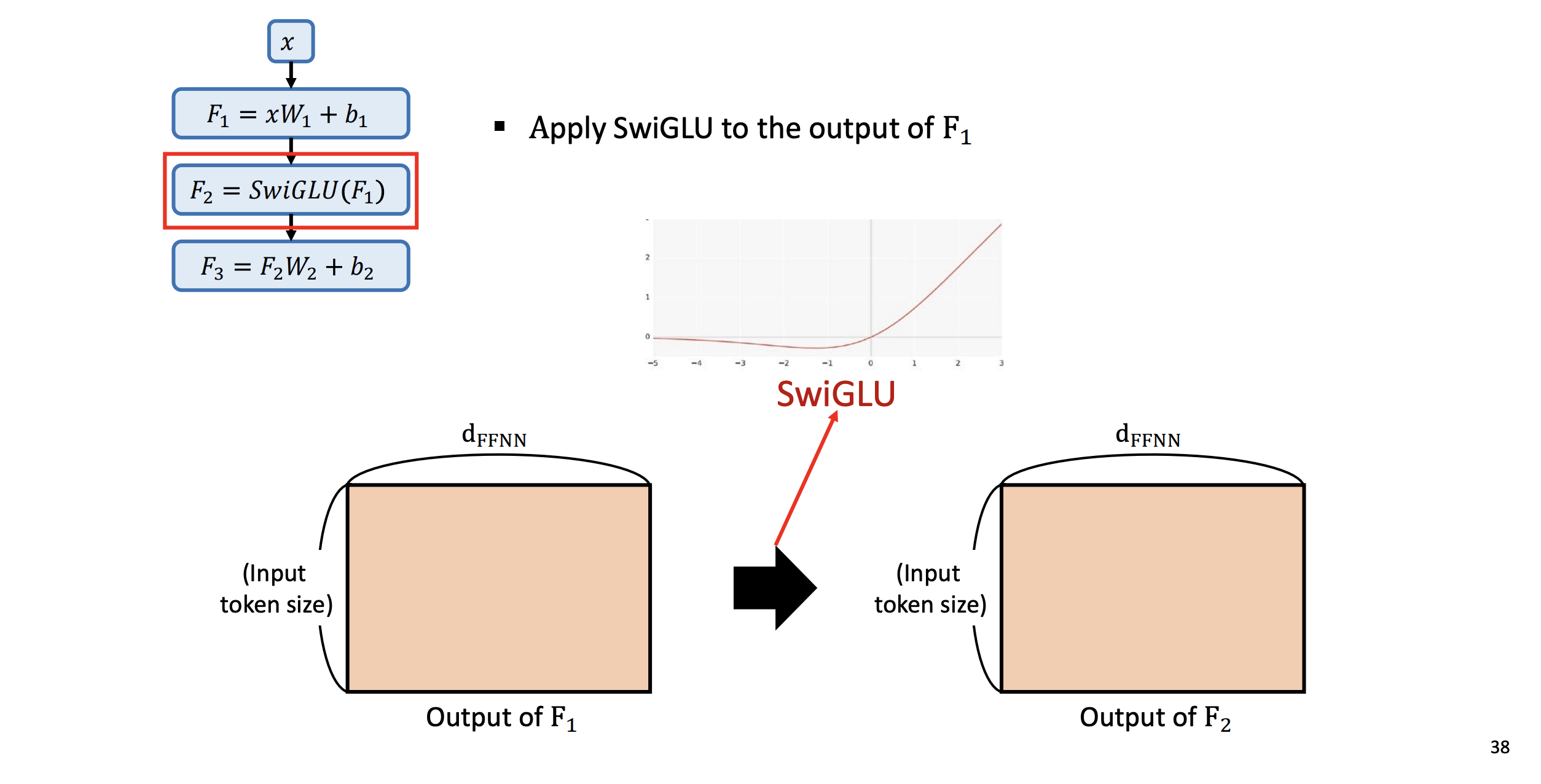
- F2 : F1 아웃풋에 SwiGLU를 적용.
- SwiGLU의 non linear 특성이 반영되면서 차원은 이전과 똑같다
- F3 : 가중치 행렬 를 사용하여 입력의 차원을 원래 모양으로 줄인다.
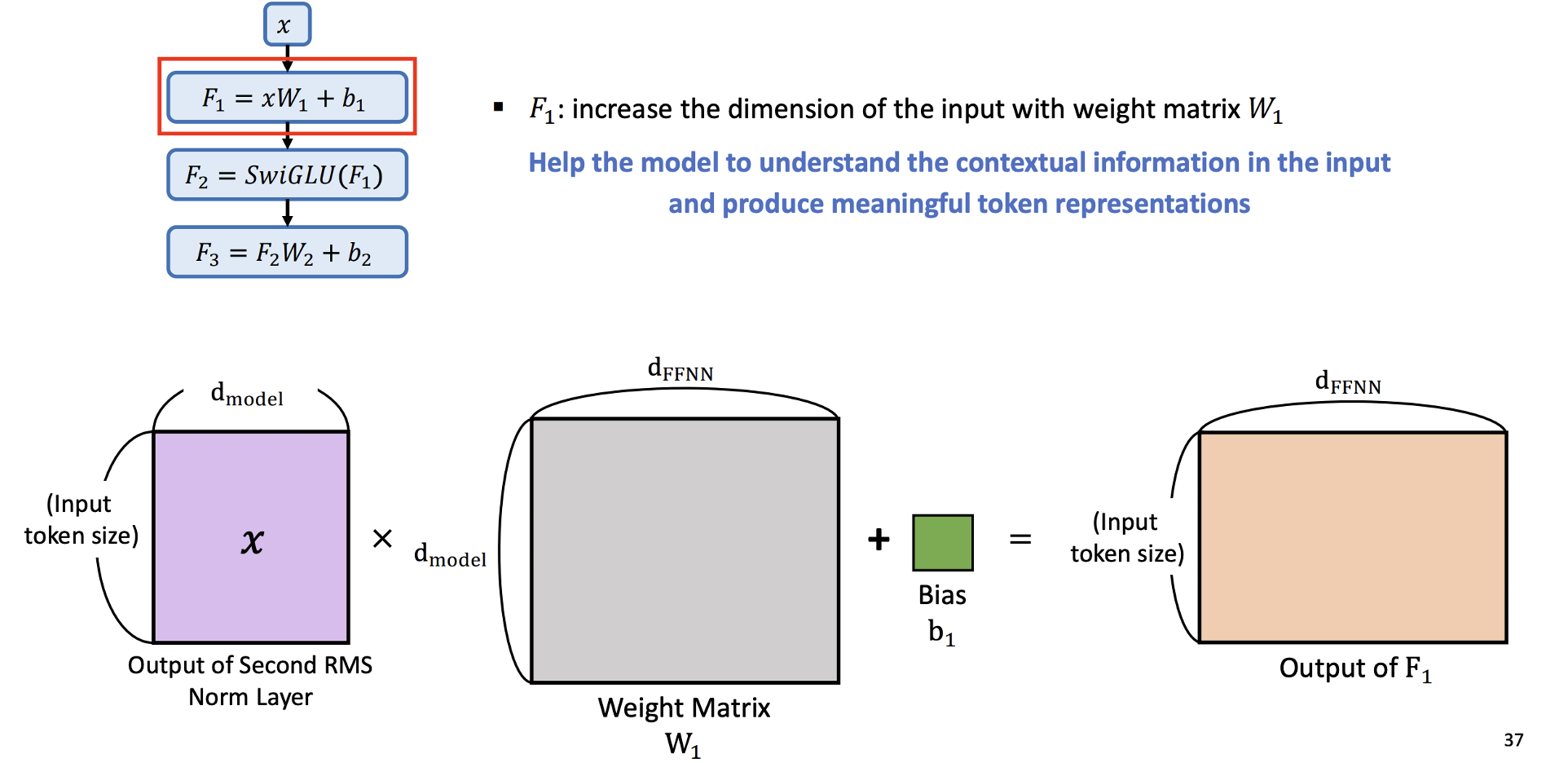
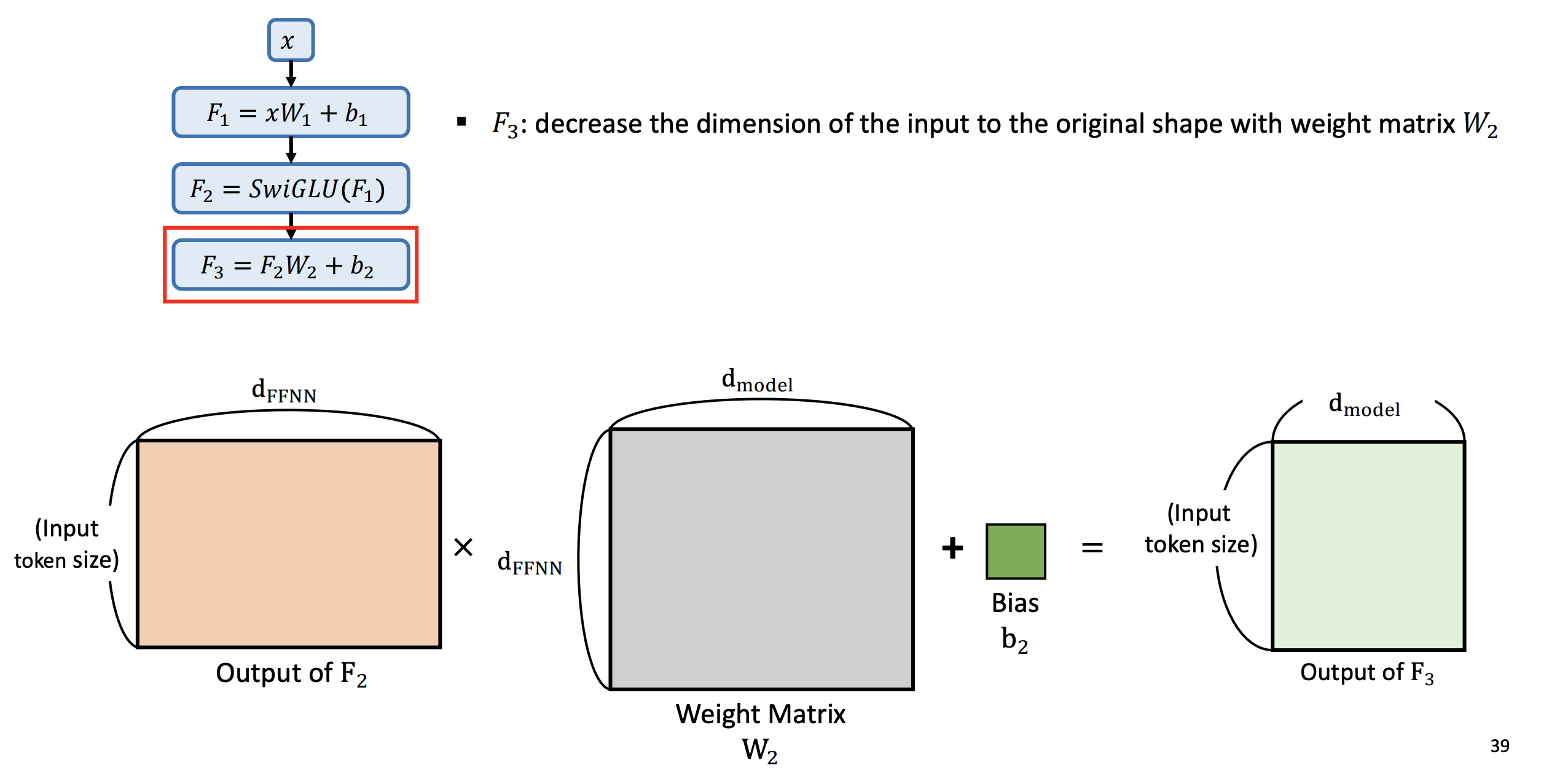
- F1 : 컴퓨팅 타임을 줄여주기 위해 가중치 행렬 을 사용하여 입력 차원을 늘린다.
(8) 세 번째 RMS Norm
- 두 번째 RMS Norm 의 결과 값과 FFNN(SwiGLU)의 결과 값과 더하여 정규화 한 것이 아래 보라색 매트릭스인 Output of Third RMS Norm Layer
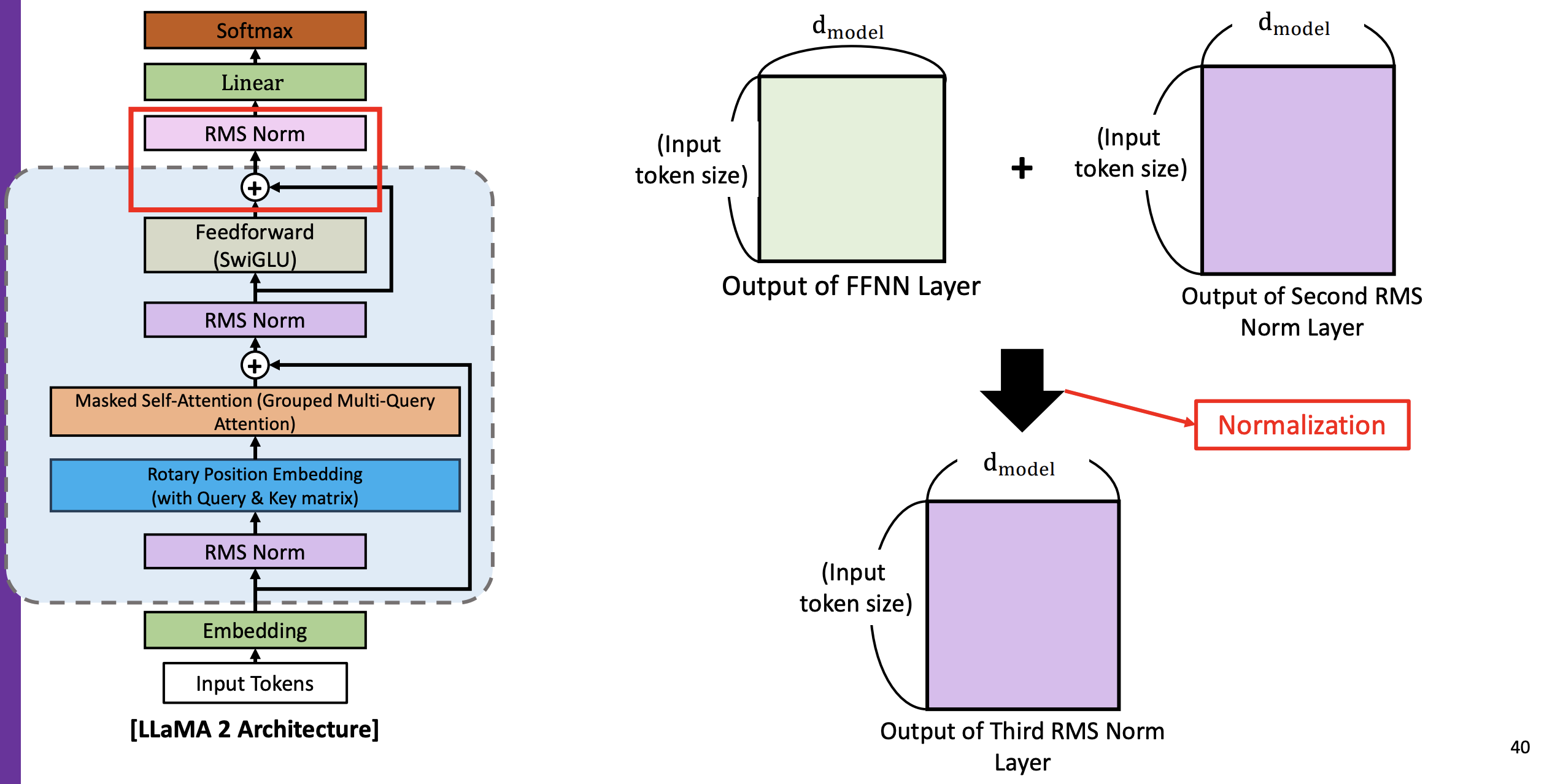
(9) Linearization
- Linear Layer
- Linearization : Linear layer 에서는 인풋의 차원을 vocab set 의 사이즈만큼 늘린다.
- 다만 weight matrix에서 디멘션을 vocab size 로 맞춰주고 곱했을 때의 계산 결과 최종적으로 vocab size가 반영된 하늘색 매트릭스가 나오는 것
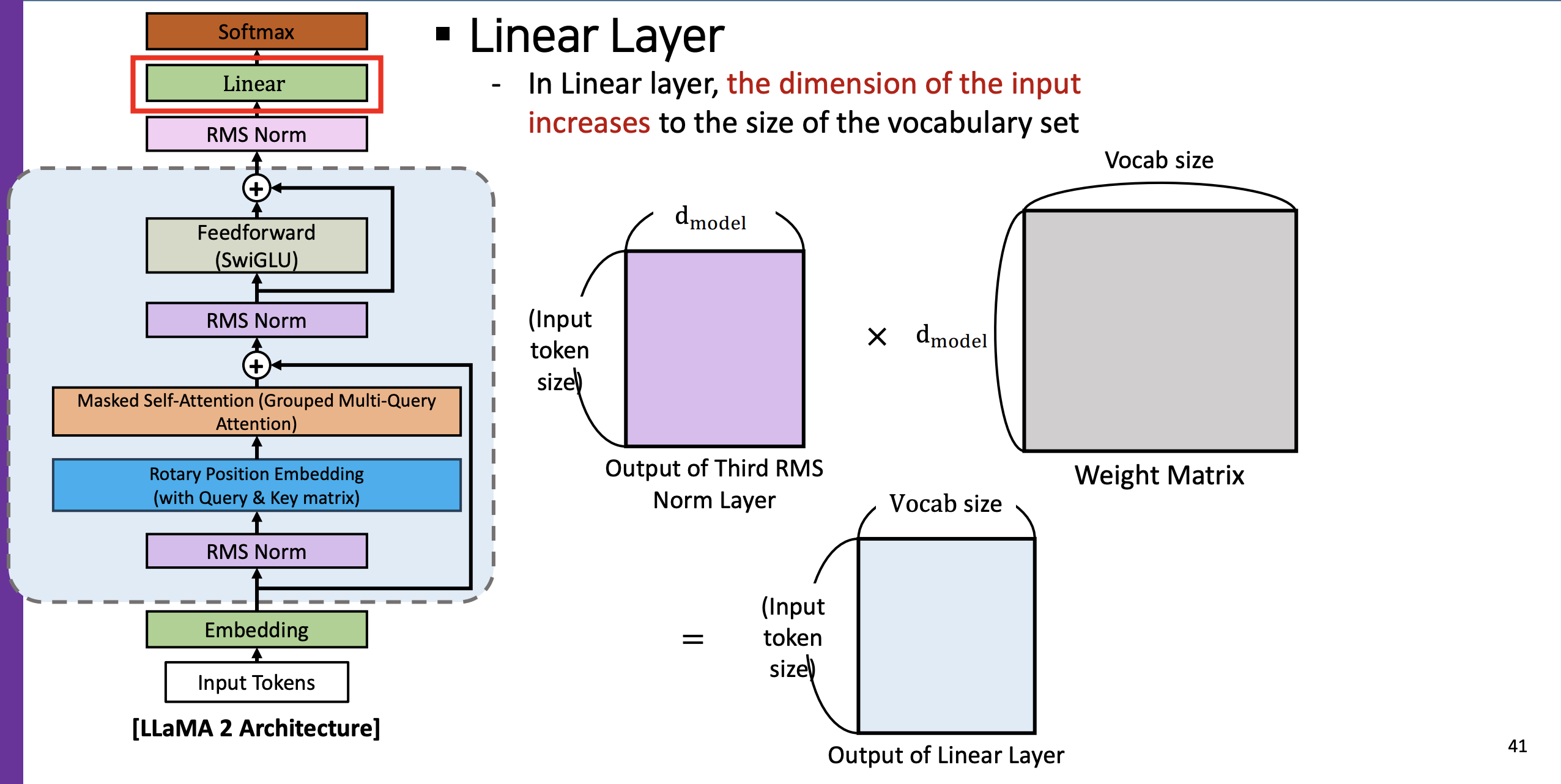
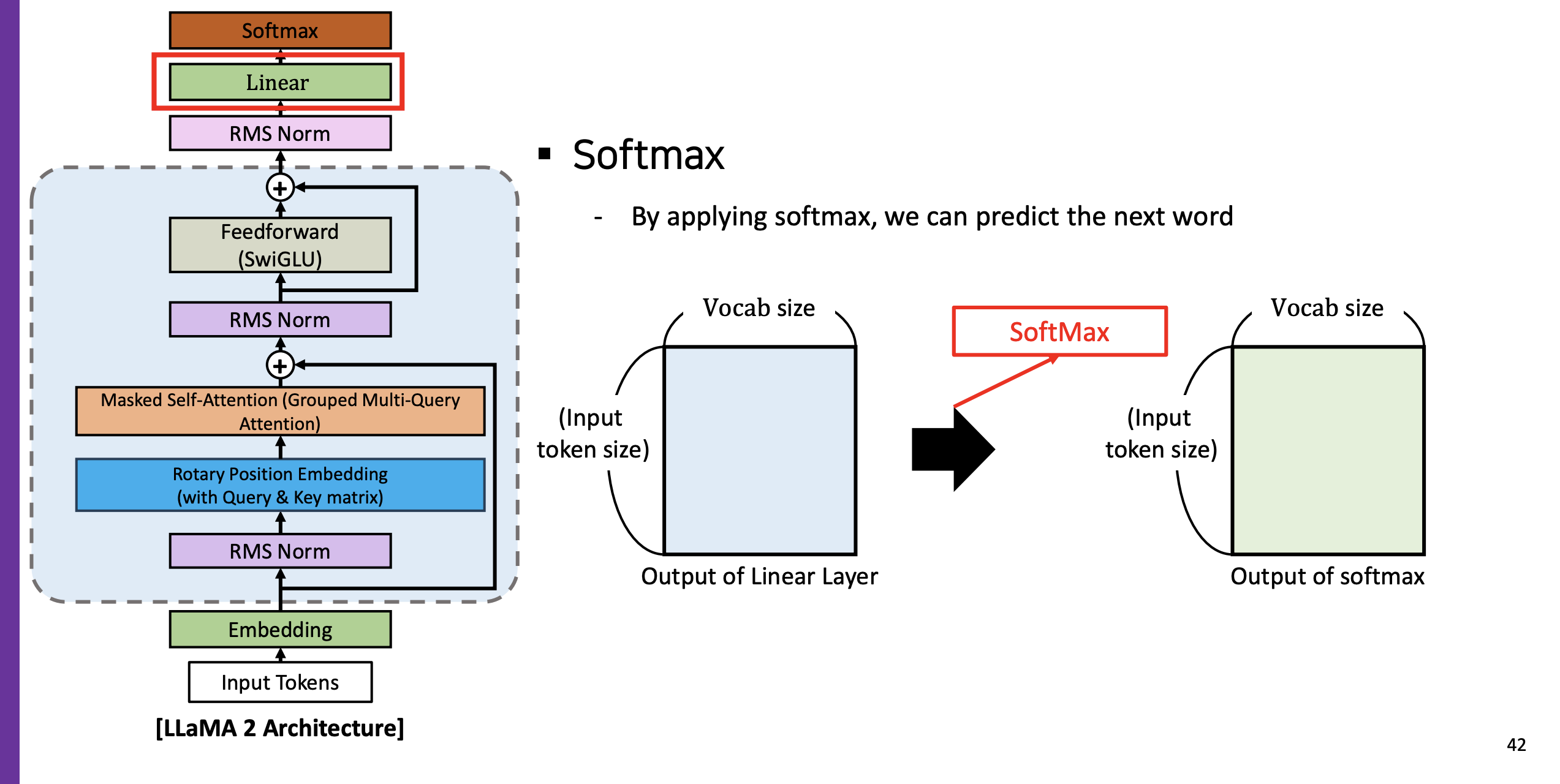
(10) SoftMax (Classification Probability)
- 최종적으로 소프트맥스를 적용하면 각 vocab 마다 어떤 확률이 나오게 된다 (분류)
- 1백만개의 supervised learning data 를 사용해서 훈련하였다
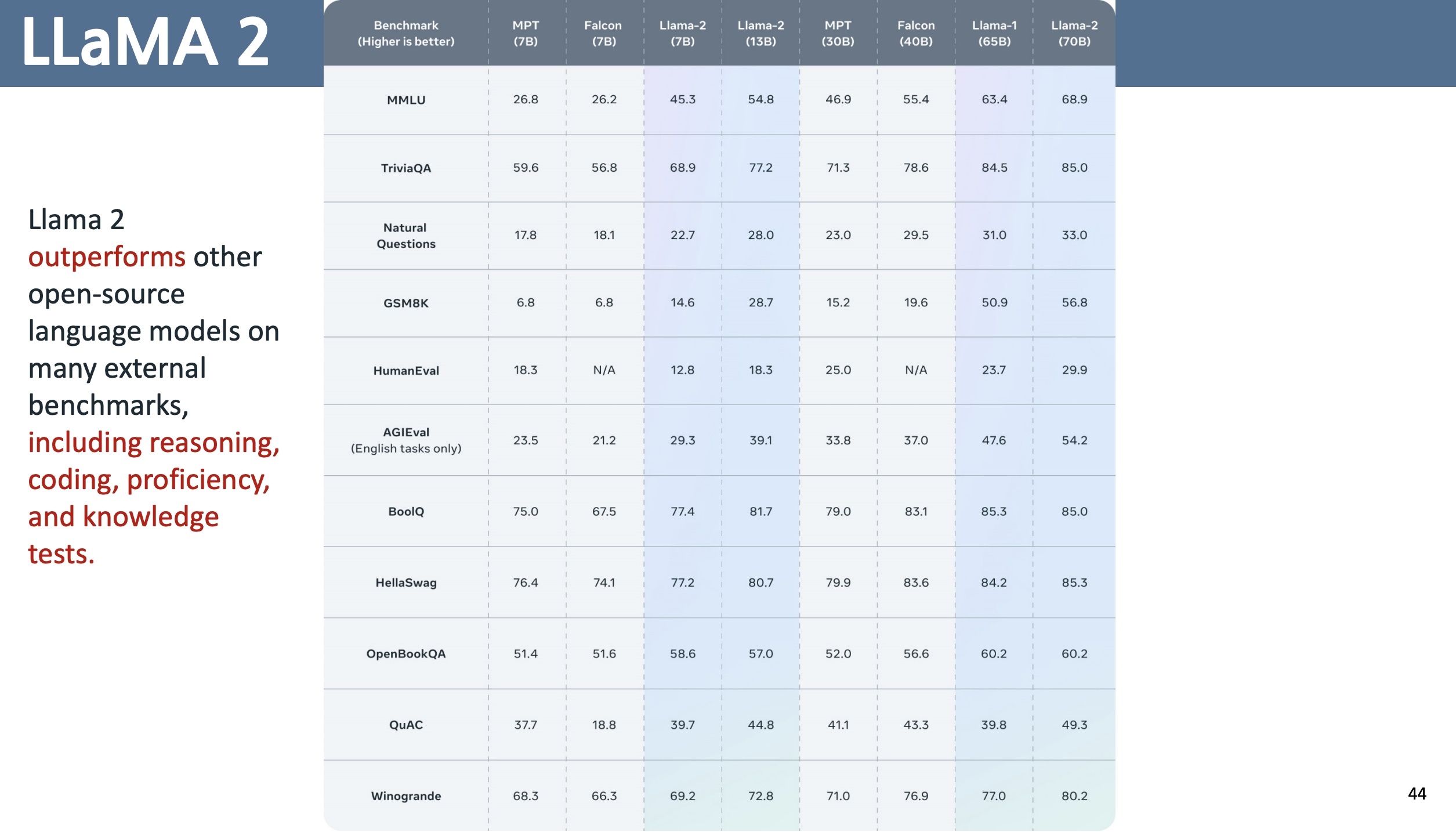
LLaMA 2 성능평가
LLaMA 1 보다 더 40% 더 많은 데이터를 사용 그리고 context length 를 두배 사용