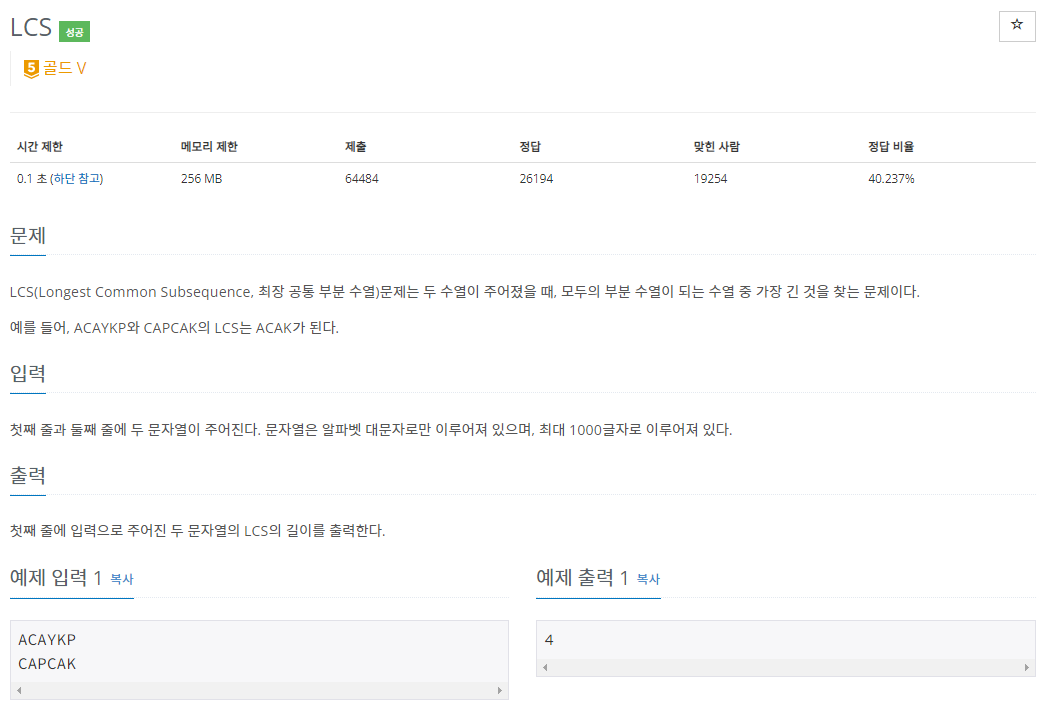
문제
https://www.acmicpc.net/problem/9251
풀이 과정
LCS : Longest Common SubSequance
말 그대로 가장 긴(longest) 공통된(Common) 부분수열(subsequance)이다. 좀 더 자세하게 말하자면 임의의 두 수열에서 각각의 부분 수열들 중, 서로 같은 부분 수열 중에서 가장 긴 부분 수열을 의미한다.
이러한 LCS문제의 경우 의외로 쉽게 접근할 수 있는데, 부분수열에서 '순서'가 지켜지기 때문에 각 문자열들의 문자들을 서로 비교하면서 서로 같으면 값을 1씩 증가시키면서 누적합을 구하는 것이다.
ex)
str1 = ACAYKP
str2 = CAPCAK
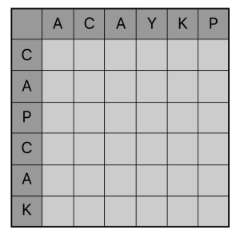
그리고 맨 앞 문자부터 차례대로 비교하여 부분수열의 길이를 누적해보자. 그럼 str1의 첫번째 문자인 A를 기준으로 str2의 문자들을 비교해보면 다음과 같다.
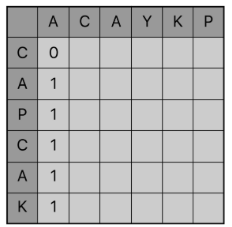
여기서 [A, A] 의 경우 {C, A} 와 {A}의 LCS 길이를 의미한다. 예로들어 [K, A] 의 경우 {C, A, P, C, A, K} 와 {A}의 LCS길이라는 것이다. 즉 두 번째 A가 오더라도 +1 더하는 것이 아니라 {C, A, P, C, A} 와 {A}의 최장 부분수열은 {A} 하나 뿐이므로 1이 된다.
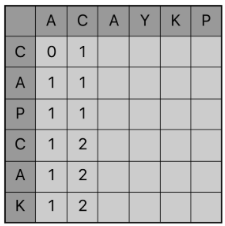
{C} 와 {A, C}의 부분수열은 {C} 이고, 두 번째 C에서는 {C, A, P ,C} 와 {A, C}의 부분 수열은 {A, C}로 +1이 증가한다.
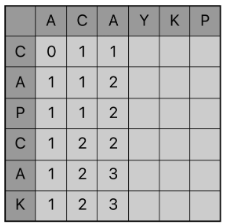
{C}와 {A, C, A}의 부분수열은 {C}이므로 1이고, {C, A}와 {A, C, A}의 부분수열은 {C, A}이다. 다음 열 Y의 경우는 겹치는 수열이 없기 때문에 이전 열의 값을 그대로 받아올 것이다. 이런식으로 채워나가다보면 다 채웠을 때 다음과 같이 된다.
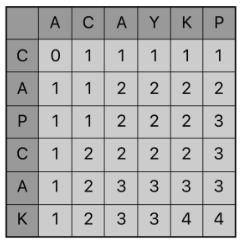
채우다 보면 규칙이 있다. 각 열을 채울 때 같은 원소가 있다면 이전 열 또는 행에 +1 한 값이 LCS 길이가 된다는 것이다.
예로들어 그림에서 (0, 1)을 보자. 이 인덱스는 {C}, {A, C}의 LCS길이를 의미하는 것이고 이는 {C}로 길이는 1이다.
그 다음 (1, 2)를 보자. 이 인덱스는 {C, A} 와 {A, C, A}의 LCS 길이를 의미하는 것이다. 즉, {C}, {A, C} 에서 'A'라는 공통 원소가 추가 된 것이다.
즉,
x번째 원소와 y번째 원소가 같다면 (x-1, y-1) 의 LCS길이의 +1이 된다.
만약 같지 않다면, 이전 행의 원소 또는 열 원소 중 '큰 것'을 기준으로 채우면 된다.
LCS(Xi, Yj) : LCS(Xi-1, Yj-1) + 1 if (Xi == Yj)
LCS(Xi, Yj) : max( LCS(Xi-1, Yj), LCS(Xi, Yj-1) ) if (Xi != Yj)
코드
Top-Down 방식
package day0216;
import java.io.*;
import java.util.*;
// LCS(최장 공통 부분 수열) Top-Down 방식
public class BOJ_G5_9251_LCS {
static char[] str1, str2;
static Integer[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
str1 = br.readLine().toCharArray();
str2 = br.readLine().toCharArray();
dp = new Integer[str1.length][str2.length];
System.out.println(LCS(str1.length-1, str2.length-1));
}
public static int LCS(int a, int b) {
// 인덱스 밖 (공집합)일 경우 0 반환
if(a < 0 || b < 0) {
return 0;
}
if(dp[a][b] == null) { // 탐색하지 않은 경우
dp[a][b] = 0;
// str1의 a번째 문자와 str2의 b번째 문자가 같은지 검사
if(str1[a] == str2[b]) {
dp[a][b] = LCS(a-1, b-1) + 1;
} else { // 같지 않다면 LCS(dp)[a-1][b]와 LCS(dp)[a,b-1] 중 큰 값으로 초기화
dp[a][b] = Math.max(LCS(a-1, b), LCS(a, b-1));
}
}
return dp[a][b];
}
}Bottom-Up 방식
import java.io.*;
//LCS(최장 공통 부분 수열) Bottom-Up 방식
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
char[] str1 = br.readLine().toCharArray();
char[] str2 = br.readLine().toCharArray();
// 공집합 표현을 위해 인덱스가 한 줄씩 추가 됨
int[][] dp = new int[str1.length + 1][str2.length + 1];
// 1부터 시작 (index 0 은 공집합이므로 0의 값을 갖고있음)
for(int i = 1; i <= str1.length; i++) {
for(int j = 1; j <= str2.length; j++) {
// (i-1)과 (j-1) 번째 문자가 서로 같다면
if(str1[i - 1] == str2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1; // 대각선 위 (i-1, j-1)의 dp에 +1 한 값으로 갱신
} else { // 같지 않다면 이전 열(i-1)과 이전 행(j-1)의 값 중 큰 것으로 갱신
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
System.out.println(dp[str1.length][str2.length]);
}
}