[논문리딩] SIRFS

풀네임: Shape, Illumination, and Reflectance from Shading

읽게된이유: Shape from shading 파트를 공부하면서 소개되어, 흥미를 가지게됨.

도대체 어떻게 이미지의 view 변화가 아닌, shading의 변화를 통해 reconstructing이 가능한 것인가? 의문을 가지게 됨.

분야: Shape from shading (Reconstructing 3D geometry from one Image)

Task:

한장의 사진으로 the most likely explanation을 가지는 intrinsic, 3D structure를 recovering하라!

---

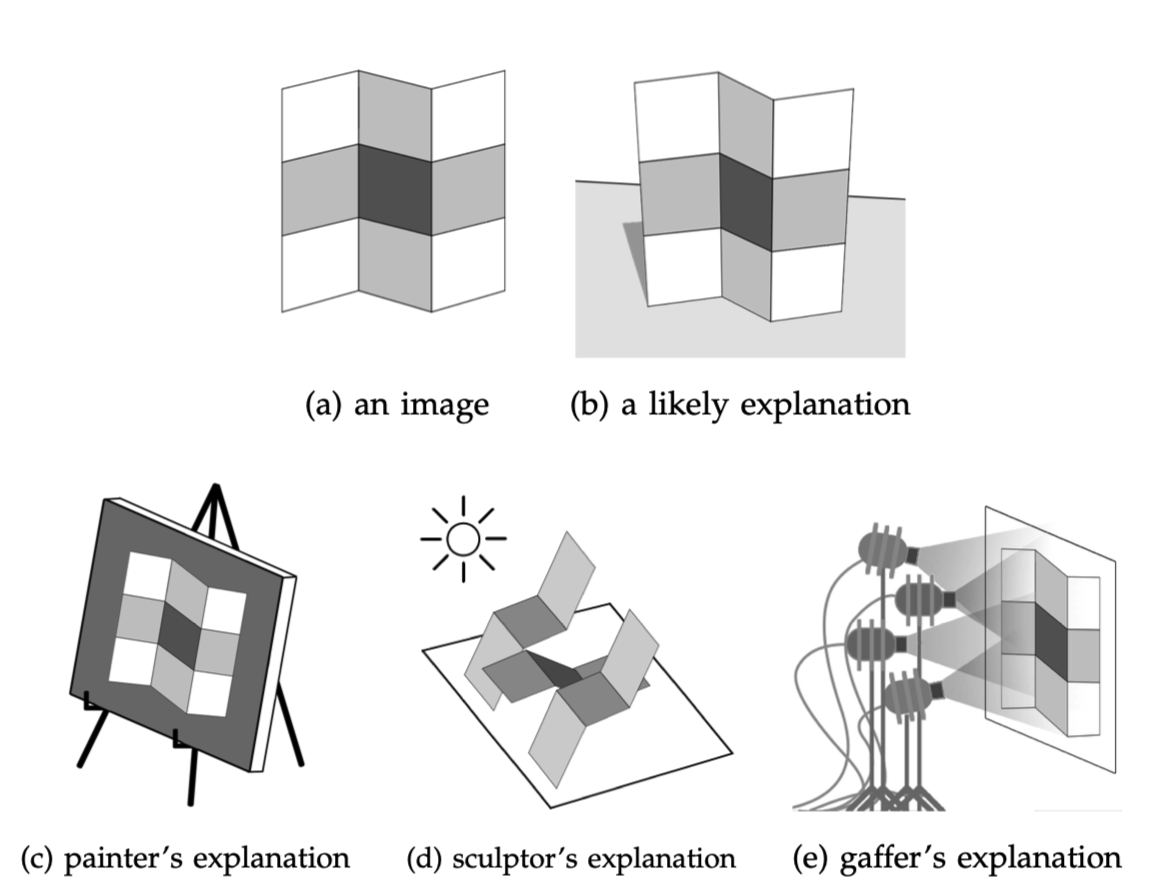
Problem formulation

---

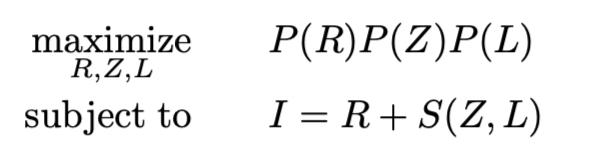
SIRFS의 문제해결법은 위와 같다.

부가설명:
R: log-reflectance image
Z: depth-map
L: spherical-harmonic model of illumination (Vector parameterizing the illumination)

S(Z,L): rendering engine ( linearizes Z into a set of surface normals, and produce a log-shading image from those surface and normals and L) -> 쉽게생각하면 Z,L에대한 렌더링 함수인 것 같다.

P(R), P(Z), P(L)은 각각, priors on reflectance, shape, illumination 에 해당한다.
아래서 각 prior들이 어떤것인지 알아볼 것이다.

목표: log-image I와, SIRFS의 모델 즉, R + S(Z,L)이 같아지도록 하는것이 목표이며,
이를 달성하기 위해서는 P(R)P(Z)P(L)을 최대화해야한다. (이는 cost function을 최소화 하는것과 같은효과)

재구성: 문제를 cost function의 시각으로 재구성하면 아래와 같다.

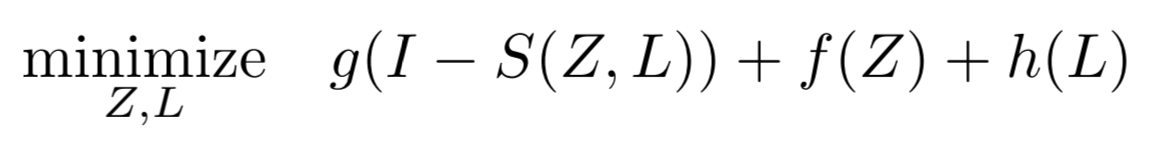
여기서 각 g, f, h함수는 R, Z, L에대한 cost function이다.
(g안에 들어간 I-S(Z,L) = R임을 위의 식에서 알수있다)

자 이제, reflectance, shape, illumination 에 해당하는 Priors들을 살펴보러 가보자.

---

Priors On Reflectance

위에서 살펴봤던 Reflectance에 대한 Cost 함수의 정체이다.

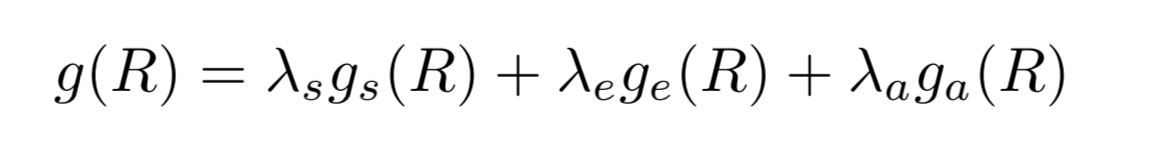
g(R)은 총 세가지 Priors(Assumption)에 의해 구성된다.

1) gs : Modeling by minimizing the local variation of log-reflectance in a heavy-tailed fashion --> Smoothness
2) ge: Parsimony of reflectance (Reflectance 절약)
3) ga: Prefering to paint the scene with some colors

g(R)을 최소화해야하기 때문에 각 Priors에대한 식들을 최소화해야한다.

---

Smoothness Prior 최소화하기

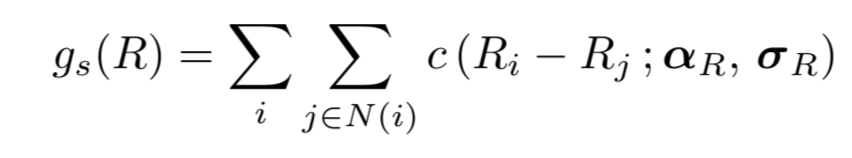
위 식에서 c는 Gaussian scale mixture의 negative log-likelihood에 해당한다.

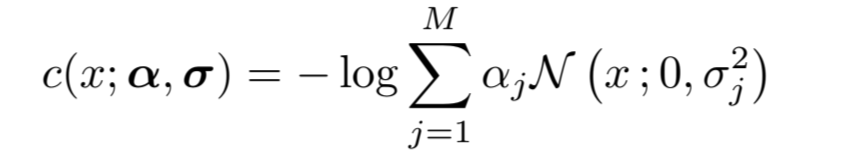
$\alpha$와 $\sigma$는 Gaussians 에서의 mixing coefficient와 standard deviation이다.

해당 논문에서는 GSM의 mean을 0으로하고 (대부분의 reflectance image를 flat하게 하기 위해), M=40으로 설정했다고 한다.

$\alpha_{R}$, $\sigma_{R}$ 은 training set을 통해 훈련된 값이다.
위 방식을 통해, 모델이 대부분 flat하고, 가끔씩만 heavy하게 변화하도록 제한을 두는 모양이다.

모델을 color image로 확장하기 위해서 아래처럼 GSM을 multivariate로 확장한다. (기존에는 univariate 였음)

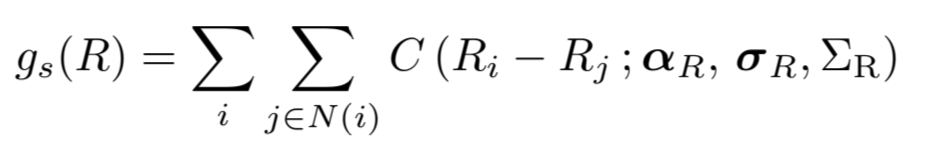
$\Sigma$ 는 GSM의 전체 covariance matrix이다.
$\alpha_{R}$, $\sigma_{R}$, $\Sigma_{R}$ 은 training set을 통해 훈련된 값이다.

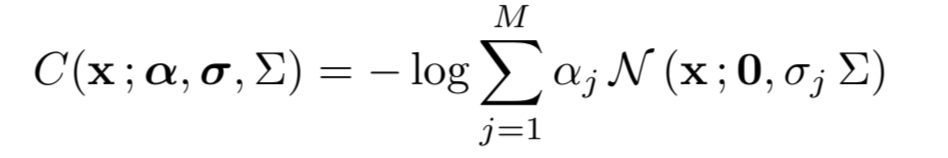
위 과정들을 통해, 반사율 차이에 대한 다양한 색상 채널의 상관관계를 확인할 수 있게되고, 모델이 반사율을 활용해서 색채변화와 음영을 사용한 무채색 변화를 설명할 수 있도록 한다고 한다.

Parsimony

이미지에 적은 양의 reflectance가 적용되도록 하고자 한다. 직역시 "절약"이라는 단어인데, 최대한 적은 양의 reflectance가 사용되도록 하는 목표를 가진다.

entropy of log-reflectance를 최소화하여 Parsimony를 실현하도록 한다.

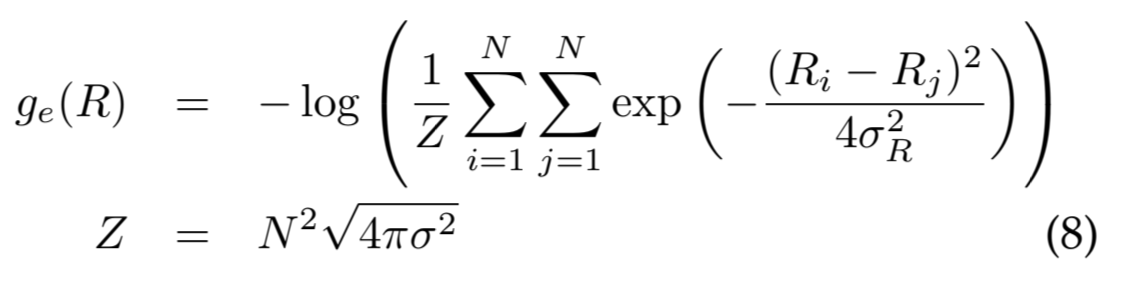
위 식을 최소화하여 얻는 효과는, 모든 reflectance pixel들이 비슷비슷한 범주 내에서 형성되도록 하는 것이다. 그렇다고해서, 모든 픽셀들이 하나의 값을 가지게되는것은 아니라고 저자는 강조한다.

또한 Parsimony와 바로 앞전에 살펴본 Smoothness가 중복되는 작업을 하는것이 아니냐는 자문자답을 한다. 결론은 둘다 필요한 상황들이 존재한다고 한다.

위 그림을 보면, c가 가장 좋은 형태의 상황인것 으로 판단된다.

지금까지의 접근방식은 gray-scale이라고 한다. 지금까지의 모델은 1차원 엔트로피 모델이고, 이를 3차원으로 순진하게 확장하는것은 좋지 못하기에, Whitening transformation이라는 방식이 적용된다.
로그반사율 이미지에서 화이트닝 변환을 미리 학습하여, 이 학습값을 통해 whitened space에서의 log-reflectance를 얻는다고 한다.

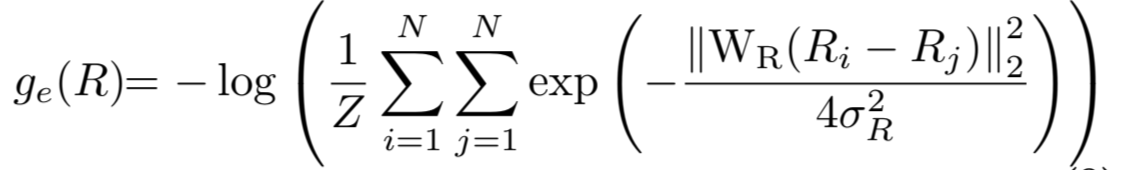
여기서 whitening transformation을 진행시키는 $W_{R}$을 구하는 과정에서, eigenvalue decomposition이 사용된다.

Absolute Reflectance

앞선 prior들은, 반사에 대한 상대적인 속성으로 부여된 것들이었다.
이 파트는, 반사율에 대한 절대적인 기준을 만들기 위한 목적이라고 이해했다.
예를들어 회색세계라고 가정한 상태에서, 회색이 아닌 경우에는 반사율에대한 penalize가 생기게 된다. color-constancy를 부여한다고 생각하면 된다.

저자는 여러 실험을 진행하여, 찾은 결과로서 regularized smooth spline을 사용하는것이 좋은 결과를 가져왔다고 말한다.

여기서도 위에서 한것처럼, grayscale images에대한 식을 작성한뒤, whitened image로 확장시키는 방법을 사용했다. (사실 여기파트는 이해하기 너무 어려워서 High Level로만 진행)

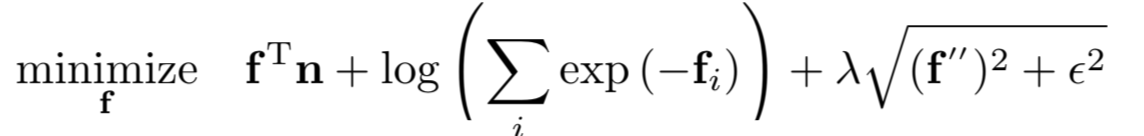
3D Spline을 사용해서, whitened log-reflectance를 훈련시킨다.

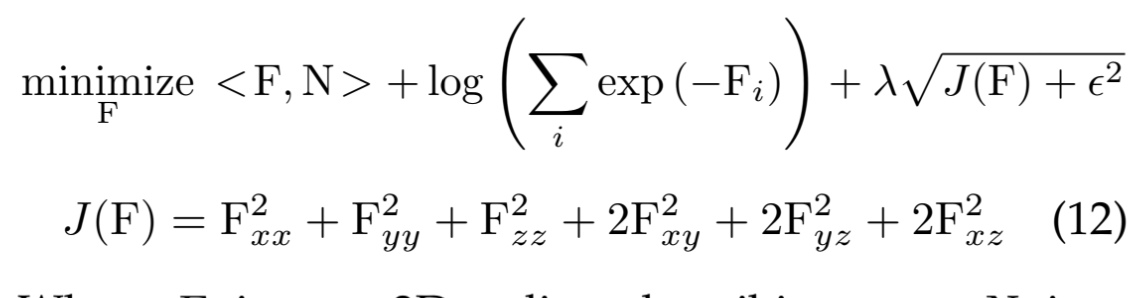
위 수식들을 최소화하는 과정을 통해, 아래 ga를 최소화할 수 있다.

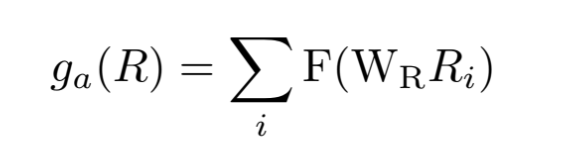
다시처음으로 돌아가서 지금까지 살펴본것이

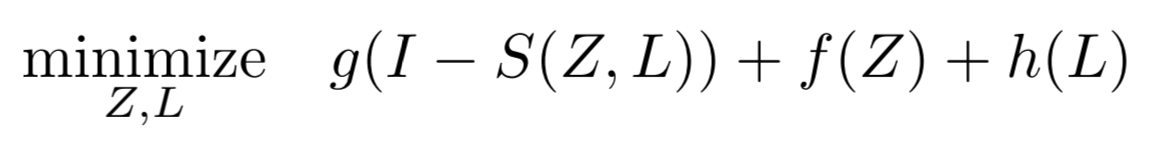
위 식에서의 g파트에 해당한다.

f, h파트는 다음시간에 살펴보자.

---

Priors on shape

shape에 대한 Cost함수의 정체.

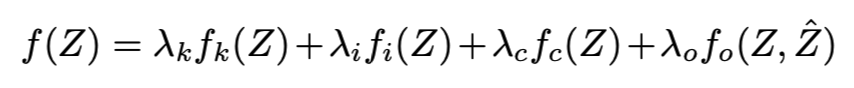
f(Z)는 총 4가지 priors에 의해 구성된다.
1) $f_{k}$: smooth prior
2) $f_{i}$: isotropy prior
3) $f_{c}$: bounding contour prior
4) $f_{o}$: encourages $Z$ to be similar $\hat{Z}$

---

smooth prior

기존의 모델링 방식중에 statistics를 활용한 방식이 주를 이루었는데, 이는 평면 회전과 scaling에 대한 불변성 문제가 있었다고 한다. 이를 해결하기 위해, differential geometry를 사용하여, 회전과 스케일에 변하지 않는 방식을 사용한다.

mean curvature라는 개념이 사용된다.
이는 avearage of principle curvatures 이며, 표면을 근사화하는데 사용된다.

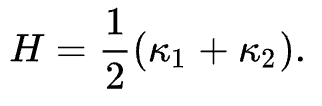
평균곡률은 또 아래와 같이 구할수도 있는데,

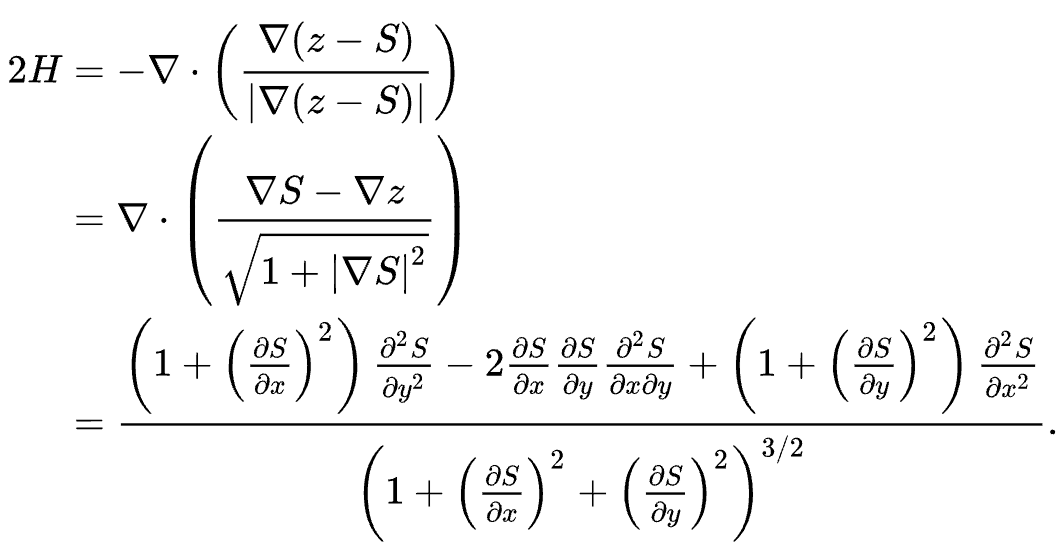
이 논문에서는, 위 식을 사용하여

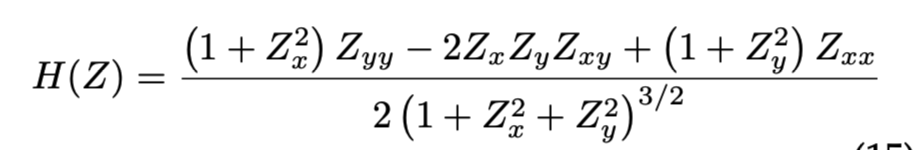
$H(Z)$를 구하고, 이를 앞서 priors on reflectance에서 본것 과 같이,
negative log-likelihood of discrete univariate Gaussian cscale mixture에 넣어준다.

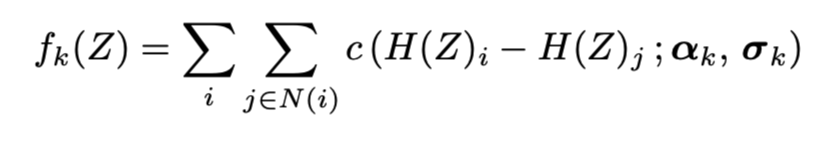
부가설명)

여기서 $N(i)$는 $i$의 5x5 인접행렬 픽셀값이고, $H(Z)$는 shape $Z$에대한 평균곡률이다. $H(Z)_{i}$ 는 픽셀 i에서의 평균곡률이 되겠다.
여기서도 미리 훈련된 $\alpha_{k}$, $\sigma_{k}$ 값을 사용한다.
여기서 사용되는 learned GSM은 매우 긴 꼬리 형식으로, shape들이 굉장히 smooth하게 잡힐 수 있도록 해준다.

isotropy

해당 prior는, 도형이 공간에서 등방성을 띠는 경향이 있다는 관찰에서 출발한다.
등방성: 물질의 중요한 특성이 방향에 관계없이 모두 동일한 상태.
해당 가정은 여러 환경에대해 valid하게 적용되는것은 아니지만, 공간에 있는 일반적인 물체의 경우 구와 유사한 경향이 있다는 점을 캐치한 것이다. 또한 관찰된 표면은 관찰자의 시선에 대해 수직이기보다는, 관찰자를 향할 가능성이 높다는 점을 적용한 것이다.

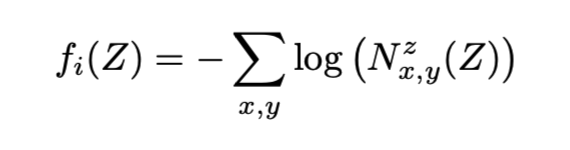
결국 식이 위와같이 되는데, $N^z_{x,y}$가 의미하는 것은, surface normal of Z 의 (x,y) 포지션에서 의 z-component이다.
저자는 위 prior가 하는 역할이, isotropic 뿐 아니라, "flatness" prior로 작용한다고 한다.

Occluding Contour

Occluding contour는 shape interpretation에 굉장히 큰 단서이다.
물체의 occluding contour에서, 표면은 모든 vantage point로부터의 ray에 접한다.
여기서는 soft version의 limb constraint를 적용한다. 이 논문에서 사용한 dataset은 masked objects로 구성되어, occluding contour $C$ 를 확인하는것은 사소한 작업이라고 한다.

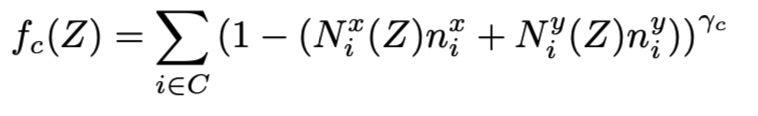
여기서 C위의 각 point i에 대하여, $n_{i}$ (local normal to the occluding contour)를 예측하고 위와같은 loss 함수를 만든다.
여기서 $N(Z)$는 $Z$의 surface normal이고, $n_{i}$와 $N_{i}$를 내적하여 1이되는 경우는 두 방향이 같을때이다. 이때 loss가 0이 된다고한다. 예측하는 값과 supplementary material에서 주어지는 $N(Z)$와 유사할수록 좋은 것이다.

Noisy Shape Observation

Shading은 상대적으로 주변것들에 대한 shape만을 표시해준다.
여기서 shape 형성에 fine-scale variaitions를 적용하면 sharp하고 localized된 변화가 적용되고, coarse-scale로 적용하면, 매우 미묘한 변화만이 적용된다. 인간이 인지하는 방식과 위 두가지 방식 모두 문제가 있기 때문에, 이를 해결하고자, 해당 prior가 적용되었다.

여기서 depth sensor를 사용하여 Z에대한 loss function을 설정한다.

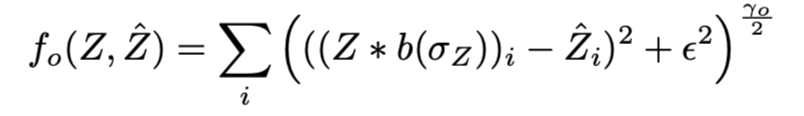
recovered depth $Z$와 raw sensor depth $\hat{Z}$가 닮게끔 한다.
여기서 b($\sigma_{Z}$)는 2D Gaussian filter로, Z와 곱해져 pixel i에서의 shape estimate Z의 blurry version의 값이라고 볼 수 있다.
어찌됐든, 실제 Z와 측정 Z가 유사해지도록 해준다.

Priors over illumination

매우 간단하다고 한다.
저자는 multivariate Gaussian to the spherical-harmonic illuminations를 자신들의 training set에 적용했다고 한다.
이는 illumination(조명)을 알 수 없기 때문에, regularized 를 한 것이다.

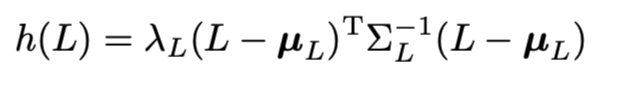
식의 형태가 차이의 제곱 꼴이다. (전형적인 loss function)

Limitation

1) Shading 자체가 shape estimation에서 매우 불리한 cue라서 모델이 종종 coarse shape estimation에서 실수를 한다고 한다.
->stereo 알고리즘이나 depth 센서를 이용해서 외부 관찰의 shape을 통합하는 방법을 제시하여 고품질의 shape estimate를 진행할 수 있음을 입증함
2) Illumination에 대한 가정에서 봤듯이, 조명이 전역적이라고 가정하여 세밀한 조명에 대한 문제를 무시하게 됨.