tree

1. 유한개(>=1)의 node로 이루어지며 root라는 특별한 node를 가지는 것

2. 용어

   1. node: tree에서 data 저장하는 기본 원소 단위
   2. root: 가장 상위의 한 개 node
   3. siblings: 동일한 parent를 갖는 node 들
   4. degree
      1. degree of node: 노드에 연결된 자식 노드 개수
      2. degree of tree: 트리에서 노드의 최대 깊이
   5. leaf
      1. degree가 0인 node
   6. internal node
      1. degree가 0보다 큰 node

   

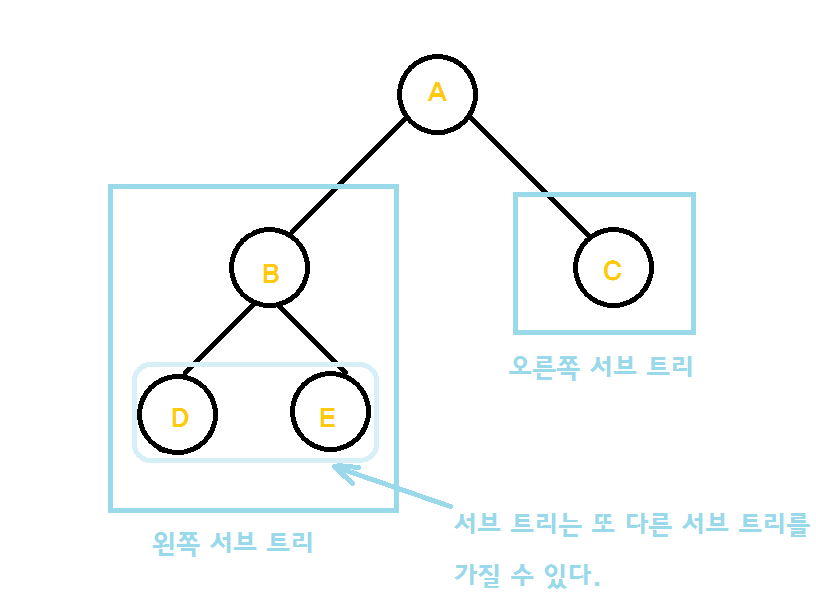
   7. subtree: 하나의 tree를 구성하는 왼쪽과 오른쪽의 tree를 의미 --> node가 한개여도 tree임
   8. ancestors: 자신과 root와의 path상에 존재하는 node들
   9. descendeants: 자신과 직접 또는 간접적으로 연결된 하위 node들
   10. level: root를 1로 했을 때 root와 상대적 거리
   11. height(=depth): 트리의 최대 깊이

binary tree 개념

1. level이 i인 node는 최대 2^(i-1)
2. height가 k인 bt의 최대 node 수는 2^k-1
3. node 수가 n인 complete bt의 height는?
   1. log2(n+1)의 ceiling
4. lemma-2
   1. n0 = n2 + 1

binary tree 구현

1. 유한개(>=0)의 node로 이루어 지며 empty거나 root와 두개의 tree로 구성
2. left-child-right-sibling --> left-first child-right-next sibling
   1. tree: data 저장 공간과 하위 nodes를 가리키는 pointer로 구성 --> 임의 개수의 child를 갖는 node 설정이 어려움(childe가 남거나 부족함) ==> binary tree로 변형!
3. complete binary trees: n개의 node가 level 순서로 모두 채워진 binary tree
4. full binary tress: 주어진 height에서 최대 node 수를 갖는 binary tree
5. traversal: 모든 노드에 대하여 중복이나 누락없이 작업을 수행(left --> right은 바뀌지 않음!)
   1. indorder: left - node - right
   2. preorder: node - left - right
   3. postorder: left - right - node(오른쪽 부터 하는 것이 아님, node의 순서만 바뀔뿐!)
   4. level-order
      1. level 순서로 root부터
      2. 동일 level에서는 left --> right
6. traversal algorithm 구현
   1. recursion 사용 --> 같은 작업을 반복
7. binary tree 구현
   1. node
      1. 데이터
      2. node *left, *right
   2. tree
      1. node_count
      2. node *root
8. Selection tree
   1. winner tree
      1. 작은 것이 이기고, 작은 것이 계속 표시되는 것
   2. loser tree
      1. 작은 것이 이기지만, 진 것(큰 것)이 표시되는 것
      2. 비교할 때 적혀 있는 것들의 비교가 아니라 진짜 winner(작은 것)끼리 비교 해야함