PCA & LDA

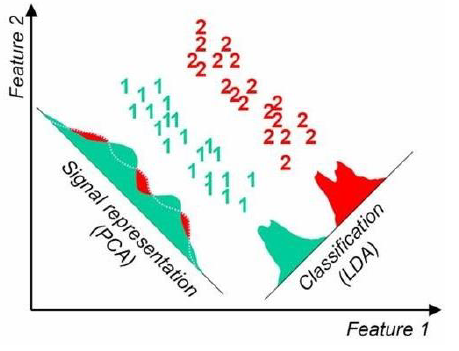
데이터셋에 대해 이야기 할 때, 차원이란 feature와 동의어입니다. 차원 축소의 기법인 PCA 와 LDA에 대해 공부하고, 두 방식의 공통점과 차이점에 대해 서술하세요.

PCA(Principal Component Analysis:주요 구성 요소 분석) :

feature값의 평균을 기점으로 Eigen value Decomposition(고윳값 분해)을 통해서 공분산 행렬, 고윳값, 고유 벡터를 구한 뒤 고유 벡터를 기준으로 한 축으로 볼 때 분산이 제일 넓게 투영된 것입니다.
이렇게 PCA를 하는 목적을 최적의 Feature를 선택한다고 해서 Feature Selection(특징 선택)이라 하거나 n개의 Feature를 n-1개 이하의 Feature로 감소시킨다고 하여 Feature Dimension Reduction(기능 차원 축소)이라고도 합니다.

LDA(Linear Discriminant Analysis:선형 판별 분석) :

기본적으로 어떤 축이 더 잘 구분했는지에 대한 척도를 측정하기 위한 목적함수는 (1) 두 클래스의 중심 간의 거리 간격, (2) 각 클래스 내의 데이터들의 분산 값 인 2가지로 분류되며, (1)인 중심 간의 거리 간격이 최대가 될수록, (2)인 클래스 내의 데이터들의 분산 값이 최소가 될 수 있도록 편미분을 통해 고윳값과 고유 벡터를 구하게 되며 구한 고유 벡터 값은 각 클래스를 가장 잘 분류해줄 수 있는 새로운 축이 됩니다.
따라서 LDA는 기본적으로 클래스를 가장 잘 구분할 수 있는 새로운 축을 찾아주기 때문에 특징으로 SVM에서 활용할 수 있으며, 또한 새로운 축을 구한 것이므로 Feature Selection(특징 선택)의 기능도 갖고 있습니다만, 해당 특징으로 인하여 '비선형 분포 데이터'에는 부적합합니다.

PCA vs LDA

PCA : 데이터가 넓게 분포(분산이 큼)되어 있도록 하는 새로운 축을 찾아 데이터를 좀 더 잘 이해합니다.
unsupervised learning에서 유용합니다.

LDA : 클래스들을 가장 잘 구분할 수 있는 새로운 축을 찾아 데이터 간의 구분이 명확하여 SVM(Clasifier)에 활용할 수 있습니다.
supervised learning에서 유용합니다.

[출처 : https://techblog-history-younghunjo1.tistory.com/66]