1주차 정리(2) Improving Deep Neural Networks : Hyperparameter Tuning, Regularization and optimization

학습을 빠르게 할 수 있는 방법

1. Normalize Input

이 방법은 실제로 인턴 당시에 구현한 서비스 모델의 train, test dataset을 가공함으로써 normalize 시킨 데이터가 더 낫다는 것을 한 번 경험했었다.

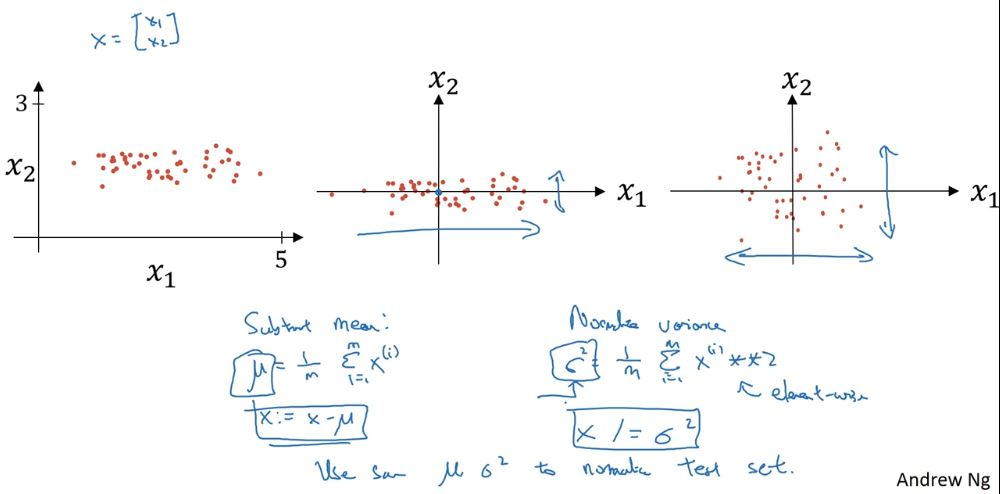
데이터를 정규화할 때, 위와 같이 모든 input에서 평균을 빼주고 제곱한 합의 평균의 제곱근으로 input을 나눠준다.

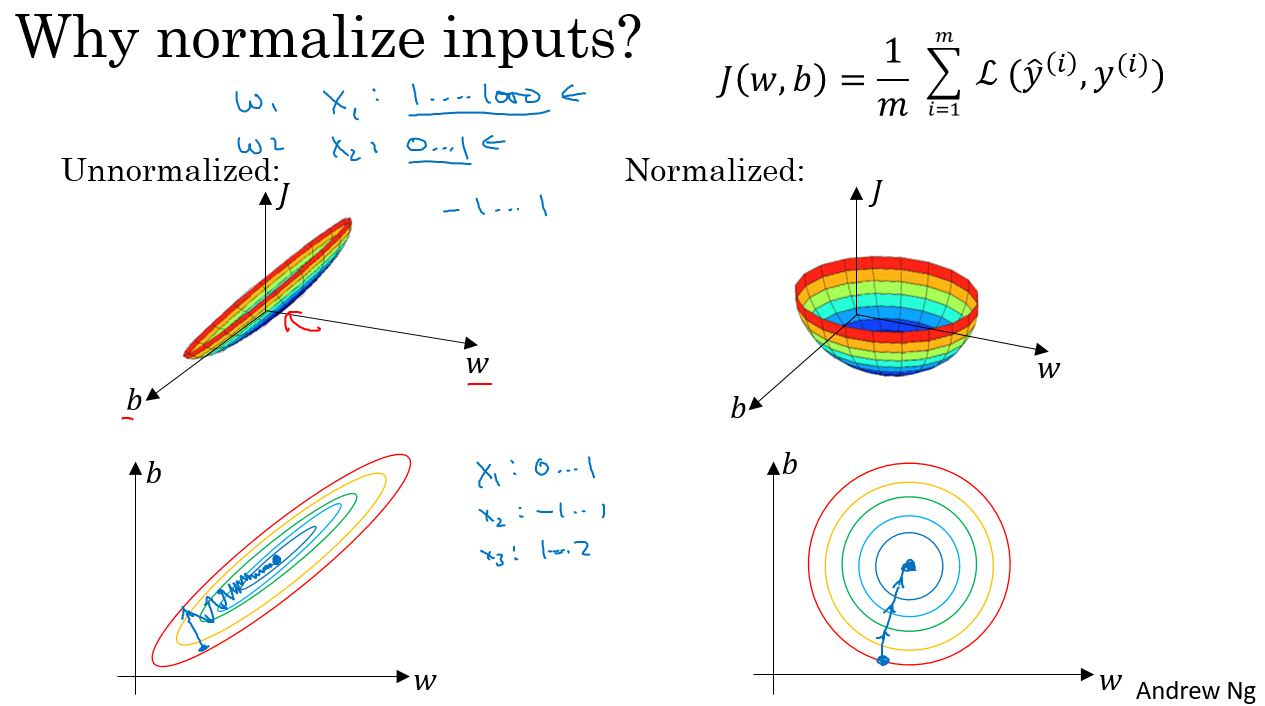
위 자료는 데이터를 정규화하지 않은 경우와 정규화한 경우다. 정규화를 하지 않은 경우는 $w1$ $w2$가 갖는 각각의 영향의 크기가 다르기에 학습하는데 어려움을 느낀다. 실제로 학습 과정을 그림으로 보아도 정규화한 경우보다 느린 경우를 볼 수 있다.

2. Weight initialization

derivative(slope or $W$)가 매우 높거나 매우 낮으면 학습에 어렵다. 그 이유는 작으면 너무 적게 학습하고 크면 너무 크게 학습하기에 optimal solution을 도출하기 어렵다.

ex)

$\begin{bmatrix}1.5&0\\0&1.5\\ \end{bmatrix}$ 가 모든 layer의 가중치라면


$\begin{bmatrix}1.5^L&0\\0&1.5^L\\ \end{bmatrix}$ = $y-hat$ 이기에 발산한다.


$\begin{bmatrix}0.5&0\\0&0.5\\ \end{bmatrix}$가 모든 layer의 가중치인 경우에도

$\begin{bmatrix}0.5^L&0\\0&0.5^L\\ \end{bmatrix}$ = $y-hat$ 이기에 수렴한다.

그렇기에 가중치를 초기화하는데 특정 방법을 쓴다고 한다

1. ReLu 일때

   W_L = np.random.randn(기존 W_L의 shape) * np.sqrt(2./n[L-1])

위 코드처럼 $\sqrt {\frac{2.}{n^{[L-1]}}}$ 를 기존 $W^{L}$에 broadcasting으로 곱해준다.

2. tanh일때

	W_L = np.random.randn(기존 W_L의 shape) * np.sqrt(1./n[L-1])

tanh일 경우, $\sqrt {\frac {1.}{n^{[L-1]}}}$ 를 곱해준다.

3. Xavier initialziation

	W_L = np.random.randn(기존 W_L의 shape) * np.sqrt(2./(n[L-1]+n[L]))

xavier initialization을 사용한다면 $\sqrt {\frac{2.}{n^{[L-1]}+ n^{[L]}}}$ 을 곱해준다.

gradient checking

back propagation을 진행하는 경우, gradient를 계산합니다. 이때, back propagation의 gradient 값을 직접 구해서 실제 값과 비교하여 오차가 너무 크진 않은지 확인해보는 과정이 gradient checking입니다.
이 과정을 거치는 이유는 실제 학습이 이상하게 진행되는지 체크해보기 위해서입니다.

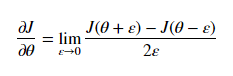
위 공식을 통해서 직접 값을 구해보는 것이고 아래 5개의 수식이 실제로 cost function과 epsilon을 활용하여 표현한 것입니다.

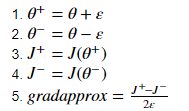
그리고 difference가 실제로 얻은 gradient 값과의 차이를 수식으로 나타낸 것입니다.

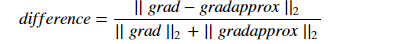
gradient checking 방식

1. $W, b , db, dW$를 하나의 큰 vector로 concatenate해준다.

gradient는 gradient 끼리 concatenate, 나머지는 나머지끼리한다.

2. $approx$와 $real$의 차이를 비교해주고 $10^-3$보다 차이가 크면 학습 과정에서 문제가 있다는 뜻으로 판단한다.

추가 사항

1. training에 쓰기에는 너무 오래 걸리기에 debug할 경우에 사용

2. regularization을 적용하고 있다면 빼먹지 말고 적용

3. dropout을 적용한 모델인 경우, gradient check할때는 turn off 후, gradient check가 끝나면 다시 적용

4. random initialization 후 train 과정을 조금 거치고 나서 gradient check을 진행 -> $W,b$가 0에 가까이 있는 경우와 멀리 있는 경우에 performance 차이가 있으면 추천