Entropy

: 정보를 표현하는 데 필요한 최소 평균 자원량

흔하게 일어나는 일일수록 정보량이 적고, 적게 일어나는 일일수록 정보량이 많다는 아이디어로 출발하여 아래 그림과 같이 정보량 표현

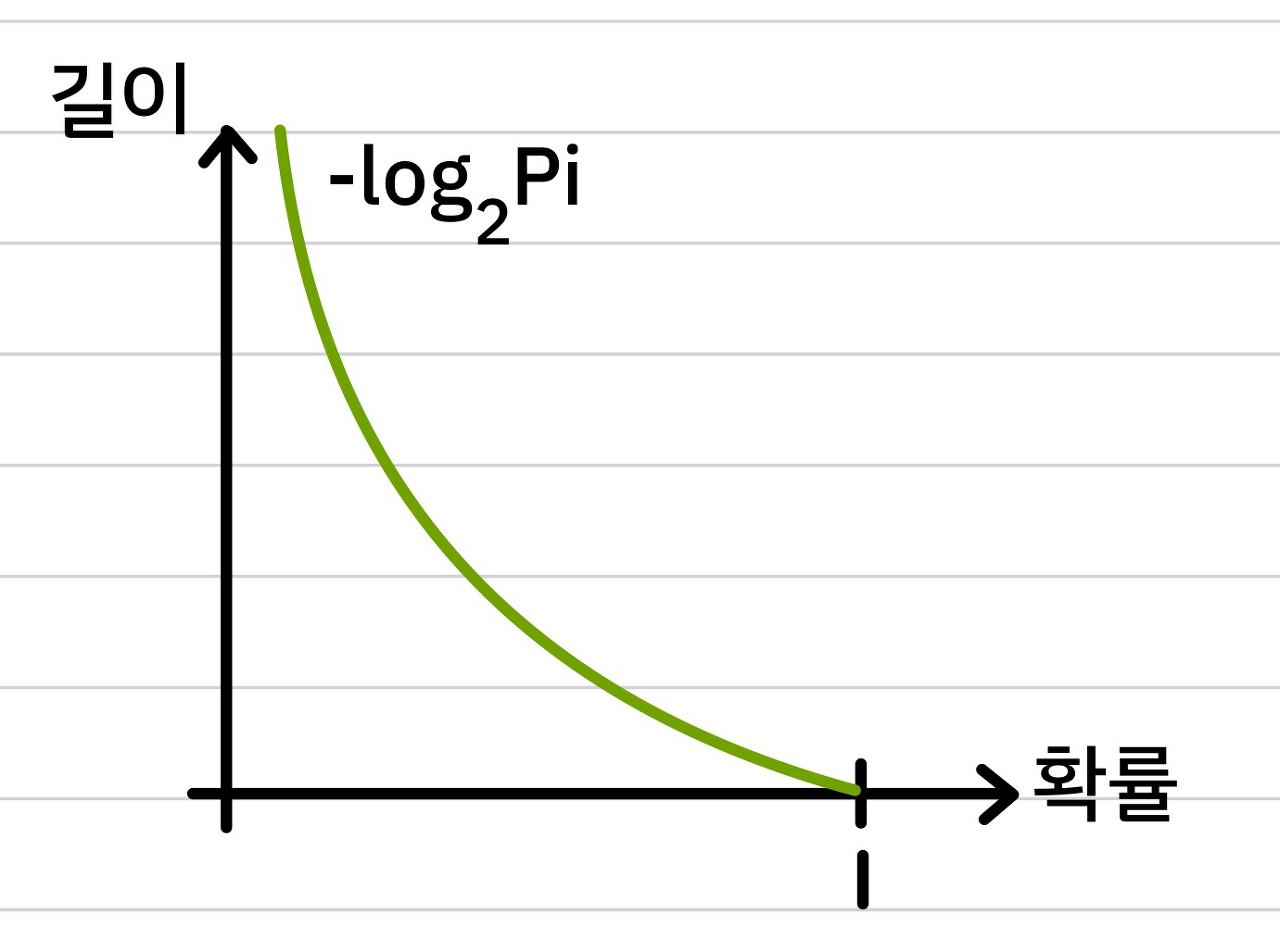
→ entropy : 불확실성 척도

→ 불확실하다 = 어떤 데이터가 나올 확률이 적다 = entropy가 높다

Cross-Entropy

: 특정 정보를 표현한 글자수의 기댓값 (현실값)

: 실제값과 예측 값의 차이를 줄이기 위한 entropy

• 실제분포 p, 예측을 통해 구한 분포 q
• 엔트로피는 이상값, 크로스 엔트로피는 현실값으로 볼 수 있음

Cross-Entropy Loss

: 보통 classification에서 머신러닝의 분류 모델이 얼마나 잘 수행되는지 측정하기 위해 사용

→ 두 개의 클래스가 있을 때의 비용함수 (로지스틱 회귀의 비용함수와 같음)

• 신경망 출력을 확률로 간주할 수 있는 경우에 사용되는 매우 중요한 손실 함수
• 비용 함수를 최소화 하는 것은 타깃 클래스에 대해 낮은 확률을 예측하는 모델을 억제 → 추정된 클래스의 확률이 타깃 클래스에 얼마나 맞는지 측정하는 용도로 사용
• cross entropy를 최소화하는 것 = log likelihood 최대화 하는 것 → cross entropy = negative maximum log likelihood estimation

KL-Divergence(Kullback-Leibler divergence)

: cross entropy와 entropy의 차이 = 정보량의 차이

KL-Divergence의 특징

1. 0이상이다.

   cross entropy가 아무리 낮아져도 Lower bound는 entropy이기 때문에 0이상

2. 거리 개념이 아니다, 비대칭적(asymmetric)이다.

   • Jensen-Shannon divergence
     $JSD(p||q) = \frac{1}{2}KL(p||M) + \frac{1}{2}KL(q||M) (where M = \frac{1}{2}(p+q))$
     • KL-divergence를 거리 개념처럼 쓸 수 있는 방법

Mutual Information

Mutual Information 정의

: 두 random variable이 얼마나 상호독립(mutual dependence)인지 찾는 방법

: joint distribution p(X,Y)가 p(X)p(Y)와 얼마나 비슷한지를 측정하는 척도

• x, y가 독립적이면 p(x,y)가 p(x)p(y)와 같아지기 때문에 log 내 식이 1 → MI = 0
• x, y가 의존적일수록 MI 값이 커짐

Mutual Information 해석

• x에 대한 uncertainty에서 y를 알고 난 후에 x에 대한 uncertainty를 뺀 값

Mutual Information과 Correlation

Mutual Information은 Correlation의 단점을 극복할 수 있다.

• correlation의 단점
  • 데이터 분포의 경사 반영 불가
  • 값이 같아도 분포가 같다고 할 수 없음
  • 선형적이지 않은 관계는 반영 불가 (only 선형)

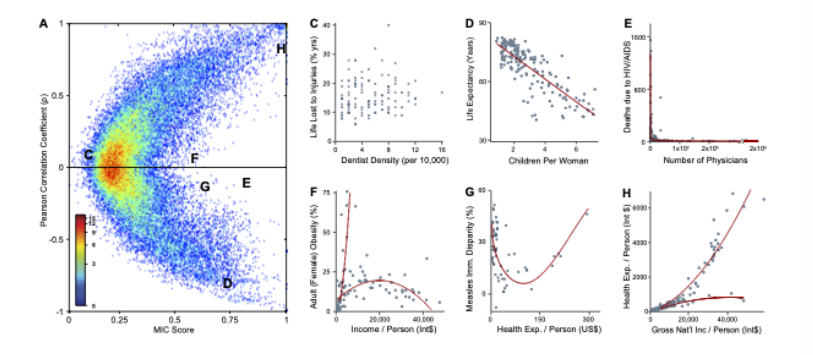
→ 선형관계만이 아닌 다양한 관계를 도출해낼 수 있음을 알 수 있음 (E, F, G)

Reference

[1] Entropy, Cross Entropy, KL-divergence 이해하기
[2] 엔트로피(Entropy)와 크로스 엔트로피 (Cross-Entropy)의 쉬운 개념 설명
[3] KL-Divergence = 정보 엔트로피 - 크로스 엔트로피
[4] Mutual Information이란?
[5] 크로스 엔트로피 손실 : 개요
[6] 핸즈온 머신러닝 2판