
15. 인공신경망
15-1. 인공신경망 (ANN : Artificial Neural Network)
: 인간 두뇌 신경의 연결 구조를 모방해 데이터를 네트워크 구조를 거쳐서 처리하도록 만든 시스템
- PE(Processing Element) : 인공 신경 세포를 노드 혹은 유닛으로 나타내는 단
15-2. 인공신경망의 구성
15-2-1. 처리 요소
- 노드(Node)
- 자신에게 입력되는 값들과 각 값의 가중치(Weight)를 받아들인다.
- 입력값(input)과 가중치를 결합해 합계를 구한다.
- 내장된 함수를 구한 합계에 적용해 출력값(Output)을 산출해 내보낸다.
- 활성함수 (Activation Function) : 임계값을 별도로 설정하는 대신에 내장된 함수를 사용해 출력값을 산출
15-2-2. 처리 요소의 결합과 계층의 결합
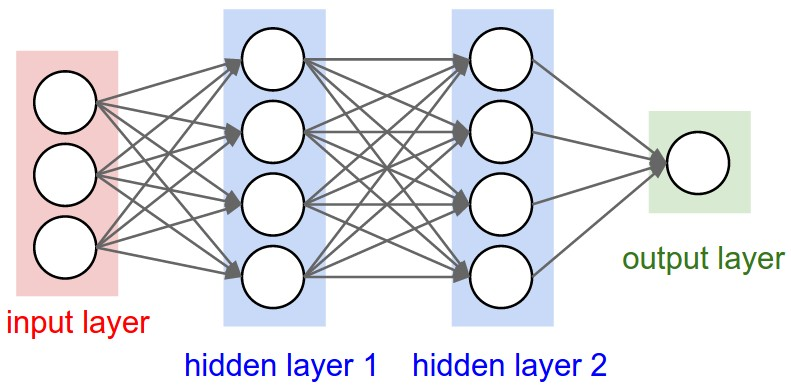
- 입력 계층 (Input Layer) : 입력값을 받아들이는 계층으로, 이 계층의 PE는 한 개의 입력값을 받아서 그대로 다음 계층으로 내보내는 역할만 한다. 즉, 입력값을 변형시키는 활성 함수가 존재하지 않는다.
- 출력 계층 (Output Layer) : ANN의 최종 출력값을 내보내는 계층이다.
- 은닉 계층 (Hidden Layer) : 입력 계층과 출력 계층 차이에 존재하는 계층이다. 입력 계층과 출력 계층은 반드시 존재해야 하지만, 은닉 계층은 없을 수도 있고 여러 개가 존재할 수도 있다.
15-2-3. 가중치와 활성함수
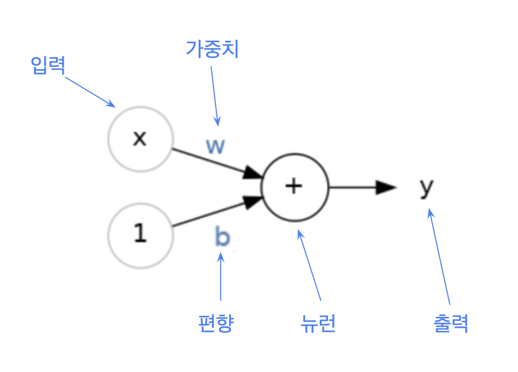
- 가중치(Weight) : 입력층에서 다음 노드로 넘어갈 때 데이터를 각기 다른 비중으로 다음 은닉층으로 전달시키기 위한 값
- 편향 (Bias) : 하나의 뉴런으로 입력된 모든 값을 다 더한 다음 이 값에 더 더해주는 상수
15-3. 역전파 알고리즘
- 전방향(Forward) 단계 : 주어진 입력값으로 ANN 출력값을 계산한 후 원하는 출력값과 ANN 출력값 간의 오차를 계산한다.
- 역방향(Backward) 단계 : 전방향 단계에서 계산된 오차를 최소화하기 위해 가중치를 수정한다.
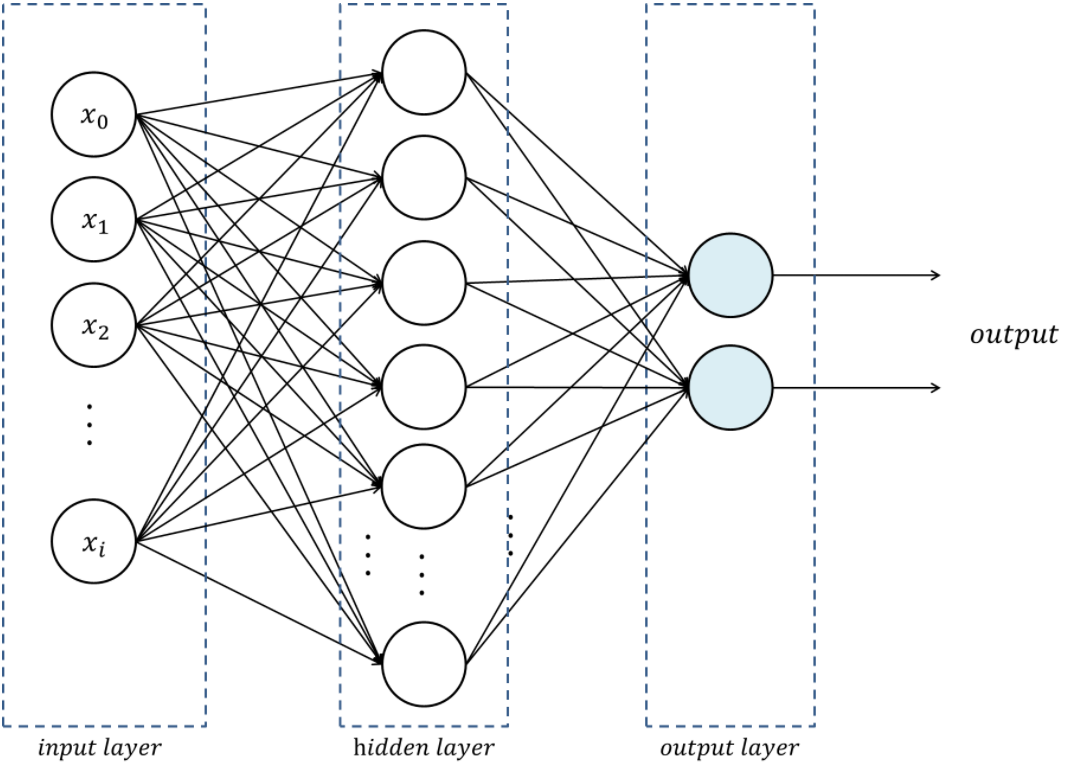
15-3-1. 전방향 단계 (forward propagation)
: 뉴럴 네트워크의 그래프를 계산하기 위해서 중간 변수들을 순서대로 계산하고 저장
- 신경망의 그래프를 계산하기 위해서 중간 변수를 순서대로 계산하고 저장함. 즉, 입력층부터 시작해서 출력층까지 처리
15-3-2. 역방향 단계
: 중간 변수와 파라미터에 대한 그래디언트(gradient)를 반대 방향으로 계산하고 저장하여 신경망을 학습시키는 방법
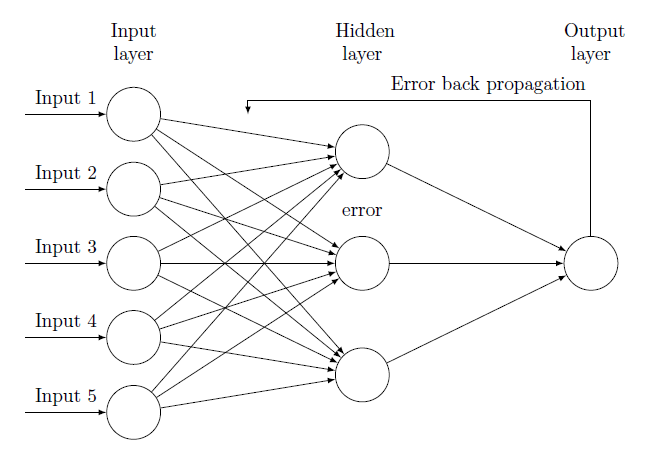
- 딥러닝 모델을 학습시킬 때 순전파(forward propagation)과 역전파 (back propagation)는 상호 의존적
- 중간 변수와 파라미터에 대한 gradient를 반대 방향으로 계산하고 저장
15-3-3. 역전파 알고리즘의 과정
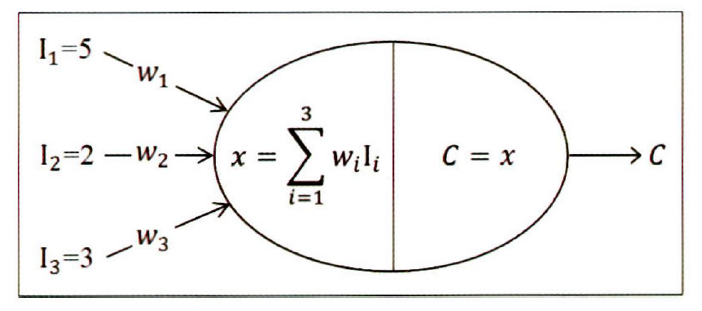
- 오차식을 그림에 맞게 쓰면
을 수정하기 위해서 으로 편미분해 기울기 구함
라고 할 때 의 기울기
새로운 가중치 식
- D=700, 초기 가중치=50, =0.02라고 설정하고 문제 풀어보기
<제1반복>- 전방향 단계
C = 505+502+50*3=500
D-C=700-500=200
- 역방향 단계
- 전방향 단계
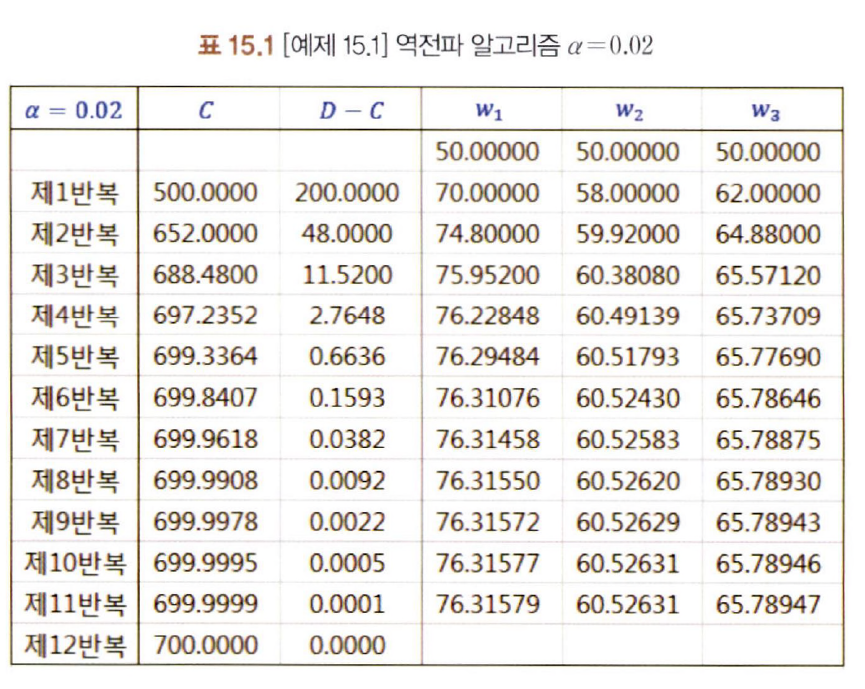
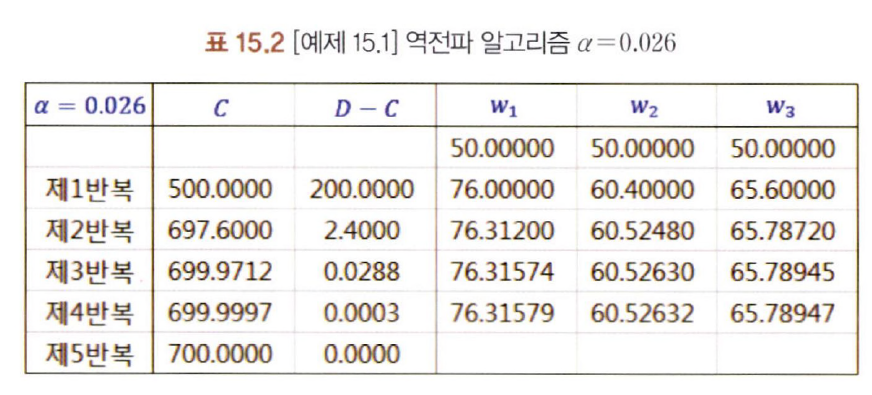
값에 따라 최적 가중치에 수렴하는 학습 반복 횟수에서 차이가 남 → 값을 적절하게 설정해야함
15-3-4. 가중치 수정의 빈도
가중치를 얼마나 자주 수정하느냐에 따라서 3가지의 방법으로 나눌 수 있음
-
배치 경사하강법 (Batch Gradient Descent)
- 한 번에 모든 입력 데이터를 사용하여 기울기를 계산하고, 그 기울기를 사용해 모델 파라미터를 업데이트
- 장점
- 전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 SGD보다 업데이트 횟수가 적음
- 병럴 처리에 유리
- 단점
- 모델 파라미터를 한 번에 업데이트하는 것이 매우 느리고, 모델 파라미터의 수가 많으면 더욱 느려질 수 있음
- 전체 학습 데이터에 대해 error gradient를 계산하기 때문에 optimal로의 수렴이 안정적으로 진행됨
-
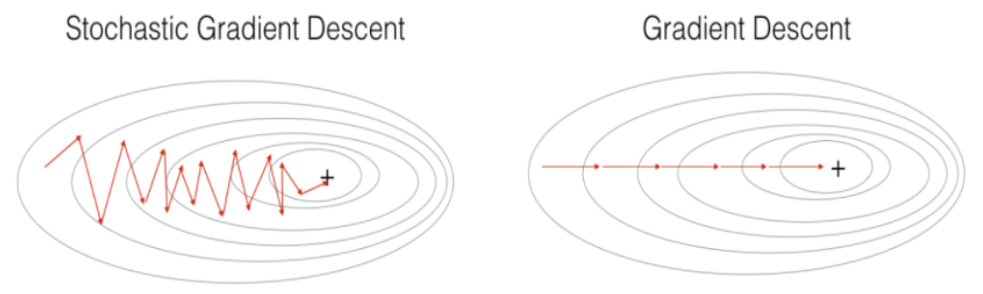
확률적 경사하강법 (Stochastic Gradient Descent : SGD)
- 학습 데이터셋에서 무작위로 한 개의 샘플 데이터셋을 추출해 그 샘플에 대해서만 기울기를 계산
- 단 하나의 데이터를 이용하여 학습하기 때문에 확률적이라고 부름
- 배치 크기가 1
- 장점
- step에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠름
- local optimal에 빠질 리스크가 적음
- 계산량이 크지 않고, 큰 데이터셋도 학습이 가능
- 단점
- global optimal을 찾지 못할 가능성이 있음
- 데이터를 한 개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
- 변동성이 큼
-
미니배치 경사하강법 (Mini-batch Gradient Descent)
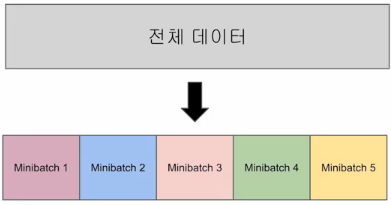
- 한 번에 모든 입력 데이터를 사용하는 것이 아니라, 일정한 크기로 나누어 여러 개의 미니 배치를 생성하여 각 배치에 대해 기울기를 계산하고 모델을 업데이트
- BGD와 SGD의 장점만 빼온 알고리즘
- 보통 SGD라고 하면 미니배치 경사하강법을 말함
- 사용자가 배치 크기를 지정
- 장점
- 계산량이 크지 않고, 가중치가 업데이트 되는 속도가 빠름
- SGD보다 병렬처리에 유리
- 단점
- batch_size를 설정해야함
- 에러에 대한 정보를 mini-batch 크기 만큼 축적해서 계산해야하기 때문에 SGD보다 메모리 사용이 높음
15-4. 활성 함수 (Activation Function)
: 출력값을 생성하여 다음 레이어로 전달하는 비선형 함수
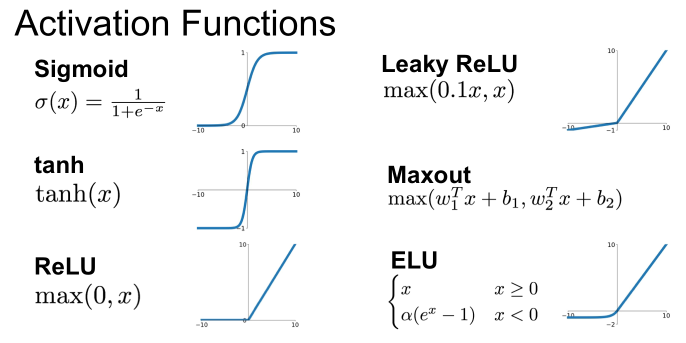
-
Sigmoid
- 큰 음수값일수록 0에 가까워지고 큰 양수값일 수록 1이 됨
- vanishing gradient problem
- 기울기는 입력이 0일 때 가장 크고, |x|가 클수록 기울기는 0에 수렴
- 역전파 중에 이전의 기울기와 현재의 기울기를 곱하면서 점점 기울기가 사라짐
- 이 문제를 해결하기 위해서 다양한 활성함수 등장
-
tanh
- 입력값이 0에 가까워질수록 0에 가까워지고, 큰 양수값일 수록 1로 수렴
- 큰 음수값일수록 -1로 수렴하기 때문에 vanishing gradient problem이 발생하지 않음 (기울기가 비선형적으로 줄어들지 않고 변화하기 때문)
- 가중치 초기값의 선택에 영향을 덜 받음
-
ReLU (Recified Linear Unit)
- 입력값이 0보다 크면 그대로 출력하고 0보다 작으면 0을 출력하는 함수
- 시그모이드 함수와 달리 -1과 1 사이에서 기울기가 0이 되지 않기 때문에 vanishing gradient problem이 발생하지 않음
- 연산 과정이 단순하기 때문에 속도도 빠름
- dying ReLU : 입력값이 0보다 작을 경우 출력값이 0이 되는 문제
- ReLU함수를 사용하는 네트워크에서 주의해야 할 문제인데 이 문제를 해결하기 위해 다양한 함수 등장
-
Leaky ReLU
- dying ReLU 문제를 해결하기 위해 등장한 함수
- 입력값이 0보다 작으면 일정한 작은 값을 출력함으로써 dying ReLU 문제 해결
-
Maxout
- ReLU 함수와 비슷하지만, 두 개의 다른 ReLU 함수의 출력값 중에 최대값을 출력하는 함수
- dying ReLU 문제를 해결하기 위해 등장한 함수로, 두 개의 ReLU 함수를 사용함으로써 기울기가 0이 되지 않음
- 역전파 단계에서 일반적인 ReLU 함수보다 더 잘 작동
-
ELU (Exponential Linear Unit)
- 입력값이 0보다 작으면 입력값에 대한 지수 함수의 값을 출력하고 0보다 크면 그대로 출력하는 함수
- ReLU보다 더 부드러운 곡선을 이뤄 dying ReLU문제가 발생하지 않는다는 장점을 가짐
- 입력값이 0보다 작으면 음수의 값을 출력해 네트워크가 많은 특징들을 학습 가능
15-5. 비선형 분류
ANN은 비선형 분류가 가능하다.
15-5-1. XOR 문제란?
- 단층 퍼셉트론으로 AND, NAND, OR 문제 해결 가능
- but XOR문제는 해결 불가능
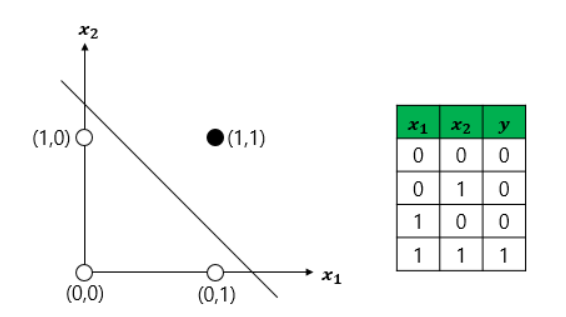
- AND GATE, OR GATE

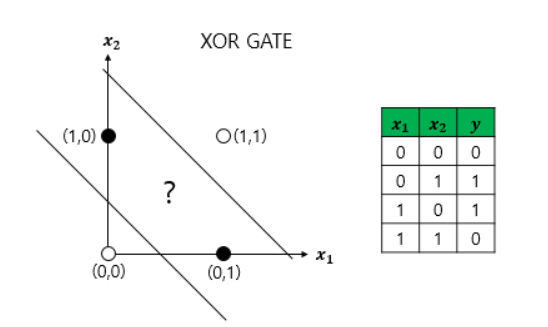
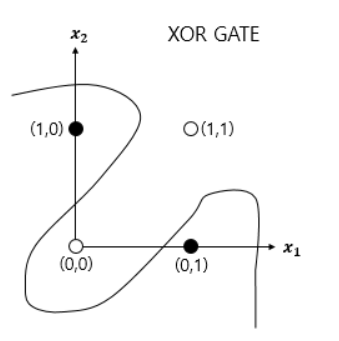
- XOR GATE
- 선형으로 분류할 수 없고 비선형으로 분류해야 해결할 수 있음
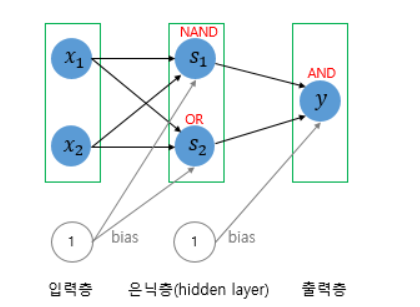
15-6. XOR 문제를 푸는 인공 신경망
- XOR GATE는 AND, NAND, OR GATE를 조합하면 만들 수 있음
- 층을 한 개가 아닌 여러개를 쌓으면 만들 수 있음
- 다층 퍼셉트론이 단층 퍼셉트론보다 더 복잡한 계산을 하기 때문에 비선형 분류가 가능
- 다층 퍼셉트론을 사용하면 XOR GATE뿐만 아니라 다양한 비선형 문제를 해결 가능
- 심층 신경망 (Deep Neural Network, DNN) : 은닉층이 2개 이상인 신경망
15-7. 범주형 속성의 인코딩
- ANN에서는 모든 데이터가 수치형이어야 하기 때문에 범주형 속성에 인코딩을 하여 ANN에 넣
- 범주형 속성이 여러 개의 값을 가질 때 인코딩을 하는 방법
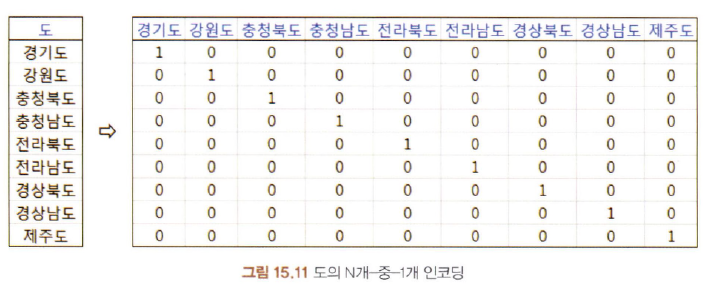
15-7-1. N개 중 1개 인코딩
- 원 핫 인코딩
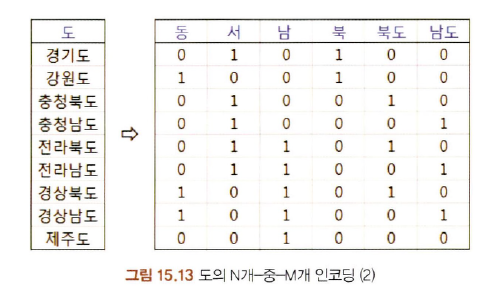
15-7-2. N개 중 N개 인코딩
15-7-3. 온도계 인코딩
- 속성이 가질 수 있는 값의 의미에 따라 그 간격을 다르게 할 수 있는 인코딩
- one-hot encoding과 비슷하지만 범주형 변수 대신 크기를 나타냄
ex)
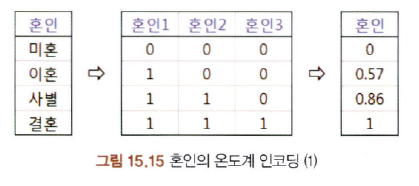
- 미혼 :
- 이혼 :
- 사별 :
- 결혼 :
Reference
[1] 데이터 애널리틱스 (이재식, 2020)
[2] CS231n
[3] WikiDocs PyTorch로 시작하는 딥러닝 입문
