[ML] 군집분석

youngchae·2023년 1월 22일

Agglomerative Clustering GMM Hierarchical Clustering KDE Mean shift clustering dbscan k-means 군집분석 데이터애널리틱스 머신러닝

데이터애널리틱스

목록 보기

3/4

본 포스팅은 <데이터 애널리틱스>를 참고하여 작성되었습니다.

9. 군집 분석

9-1. 군집 분석

군집 : 데이터 집합 내에 존재하는 의미 있거나 유용성 있는, 또는 의미도 있고 유용성도 있는 그룹
군집 분석 : 레코드들로 이루어진 데이터 집합을 그 레코드를 구성하는 속성 정보만 사용해 그룹으로 나누는 기법
클러스터링 (Clustering : 군집화) : 군집 분석 기법을 사용해 군집을 찾아내는 과정

9-1-1. 분류와의 차이점

분류 : 레코드들을 이미 알려진 또는 미리 구분해 놓은 클래스에 할당
클러스터링 : 어떠한 클래스가 존재하는지 알지 못하는 상태에서 레코드들을 그 속성 정보만 사용해 그룹으로 나눔 → 후에 레코드들의 특징을 분석해 의미 파악

9-2. 군집의 의미

같은 군집에 속한 레코드들끼리는 서로 비슷하고 다른 군집에 속한 레코드들과는 서로 달라야함
많은 경우 군집의 의미를 명확하게 해석하기는 어려움, 만족스러운 의미의 군집을 얻을 때까지 군집 수를 바꿔가며 클러스터링 작업 반복

9-3. 근접성 (Proximity)

군집을 구성하기 위해서는 레코드 간의 근접성 또는 유사성을 파악해 결과에 따라 레코드들을 하나의 군집에 모아야함

9-3-1. 수치형 속성

레코드를 구성하는 n개의 속성이 모두 수치형 → n차원 공간의 한 점으로 표시될 수 있음
근접성 구하는 가장 일반적인 방법 → 유클리드 거리 (Euclidean Distance)

9-3-2. 범주형 속성

수치형 속성으로 변환할 수 있으면 Euclidean Distance로 근접성 구하기 가능

ex) 직급 속성의 수치화

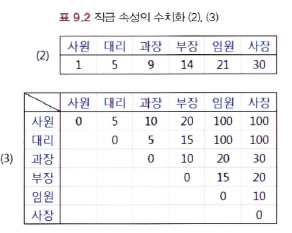
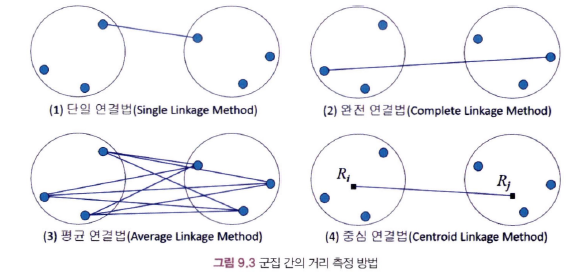
9-3-3. 군집 간의 거리 측정

단일 연결법 (Single Linkage Method) : 두 군집 간에 가장 가까운 레코드 간의 거리 측정
완전 연결법 (Complete Linkage Method) : 두 군집 간에 가장 먼 레코드 간의 거리 측정
평균 연결법 (Average Linkage Method) : 두 군집 간 레코드의 모든 쌍의 거리를 구한 후 그 평균 측정
중심 연결법 (Centroid Linkage Method) : 두 군집의 중심 간의 거리 측정

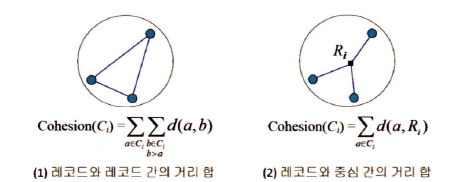
9-4. 클러스터링 결과의 평가 척도

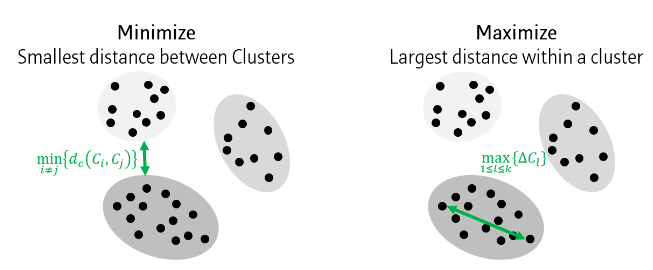
응집도(Cohesion) : 하나의 군집 안에 있는 레코드들이 서로 얼마나 근접해 있는가를 나타내는 지표
- 응집도가 작을수록 우수한 군집

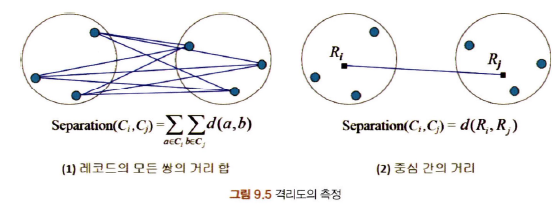
격리도(Separation) : 하나의 군집이 다른 군집들과 얼마나 잘 분리되어 있는지를 나타내는 지표
- 격리도가 클수록 우수한 군집

군집 내 응집도를 최대화하고(maximizing cohesion within cluster, maximizing separation between clusters), 군집 분리도를 최대화하여야 함

실루엣 계수 (Silhouette coefficient) : 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집화 돼 있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리돼 있는지를 나타내는 지표
- 응집도와 격리도를 모두 측정하기 위한 측정지표
- $s(i) = \frac{b(i)-a(i)}{max(a(i),b(i))}$
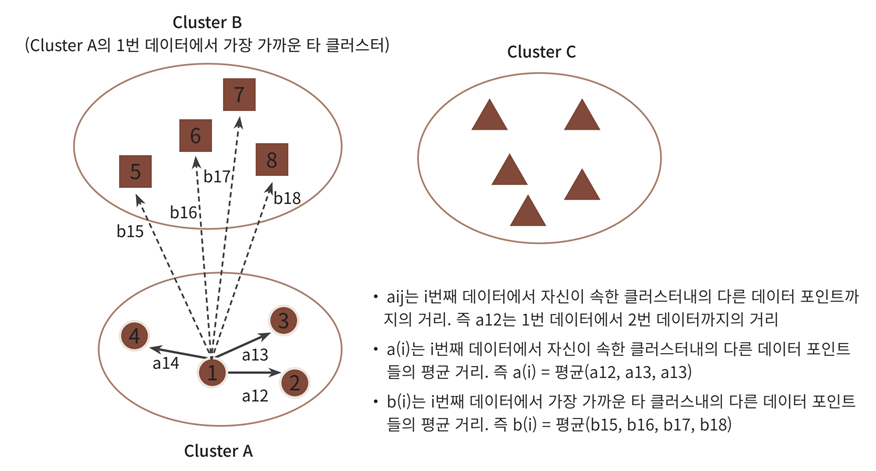
  - a(i) : 해당 데이터 포인트와 같은 군집 내에 있는 다른 데이터 포인트와의 거리를 평균한 값
  - b(i) : 해당 데이터 포인트가 속하지 않은 군집 중 가장 가까운 군집과의 평균 거리
- -1~1의 범위를 가지며 1에 가까울수록 좋은 값
Dunn Index
- 클러스터간 거리 중 최소값과 클러스터내 거리 중 최대값의 비율
- $I(C) = \frac{min_{i \neq j}\{d_c(C_i,C_j)\}}{max_{1<=l<=k}\{\Delta C_l\}}$

9-5. 클러스터링을 위한 데이터 준비

9-5-1. 속성값 조정

속성값 조정(Scaling) : 서로 다른 속성이 다른 단위와 다른 값의 범위 내에서 측정된다는 사실을 고려해 속성값을 일관성 있는 규칙에 의해 바꾸는 것
두 레코드 간의 거리가 의미를 가지려면 각 속성의 수치가 동일한 척도로 변환되어야 함
scaling 방법 종류
- 정규화(Normalization) : 모든 feature가 0과 1 사이에 위치하도록 데이터를 변경하는 방법
  - $x' = \frac{x-Min}{Max-Min}$
- 표준화(Standardization) : 각 피처의 표준편차와 평균으로 값을 정규화 (평균이 0, 분산이 1인 값으로 변환)
  - $x' = \frac{x-\mu}{\sigma}$
- 지표화(Indexation) : 평균으로 나눈 값을 사용
  - $x' = \frac{x}{u}$

9-5-2. 가중치 부여

가중치 부여(Weighting) : 속성의 중요성이 서로 다르다는 점을 고려해 속성의 상대적 공헌도를 다르게 부여하는 것
속성값 조정 작업이 끝난 후 수행해야함

9-6. 계층적 클러스터링 (Hierarchical Clustering)

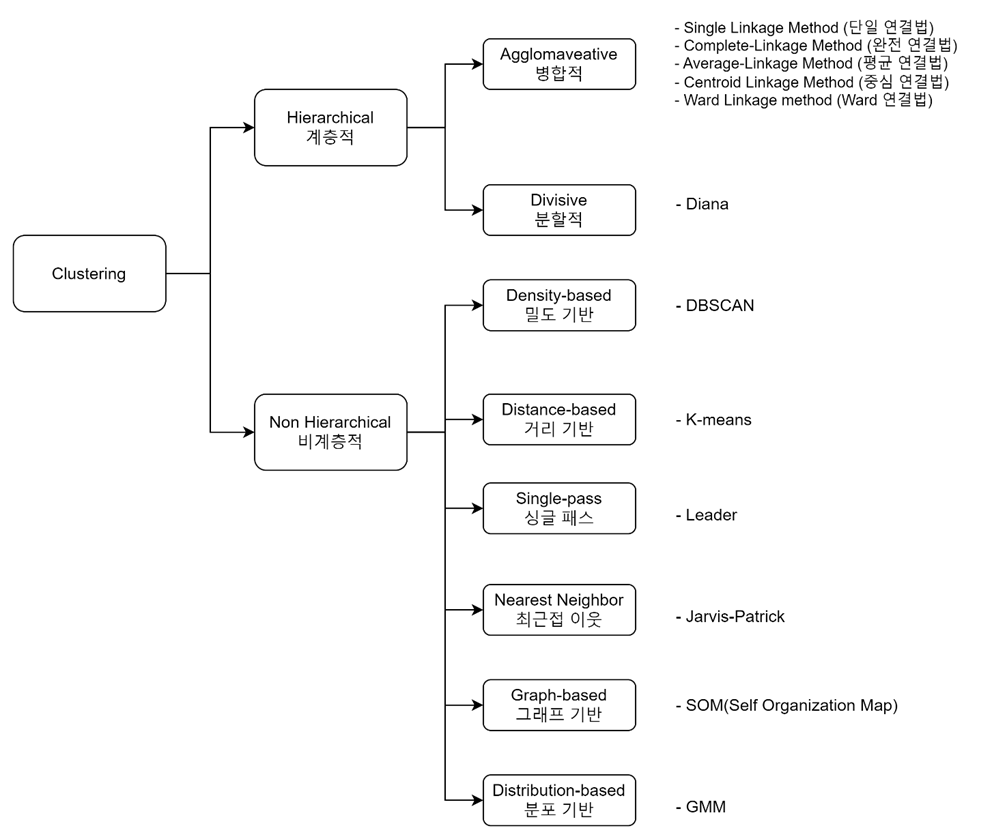
계층적 클러스터링(Hierarchical Clustering) : 레코드 간의 거리를 측정해 가까운 것끼리 모아 군집을 구성하는 방법
- 군집 안에 부분 군집 존재
비계층적 클러스터링(중심기반 클러스터링=분할적 클러스터링 : Non Hierarchical Clustering = Partitional Clustering): 군집의 중심과 레코드 간의 거리를 측정해 거리가 가까운 중심의 군집에 레코드를 할당하는 방법
- 군집간 부분집합이나 중복없이 상호배타적(exclusive)으로 존재

9-6-1. 병합적 클러스터링(Agglomerative Clustering)

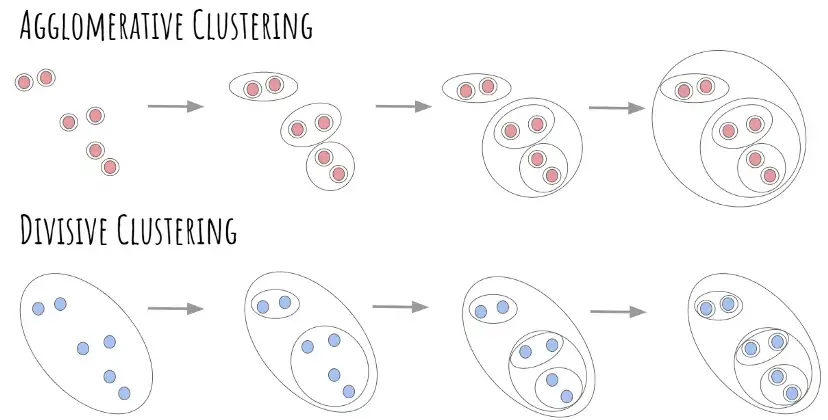
데이터에서 시작해서 유사한 데이터끼리 순차적으로 군집을 묶어나가는 알고리즘 (Bottom-up)
반복 횟수가 증가할수록 합쳐지는 군집 간의 거리는 점진적으로 증가 (단조로운 증가)
- but 중심 연결 클러스터링에서는 거리가 반드시 증가하지는 않음
  - 전도(Inversion) : 반복 횟수가 증가하는데 군집 간의 거리가 감소하는 현상

수행 단계

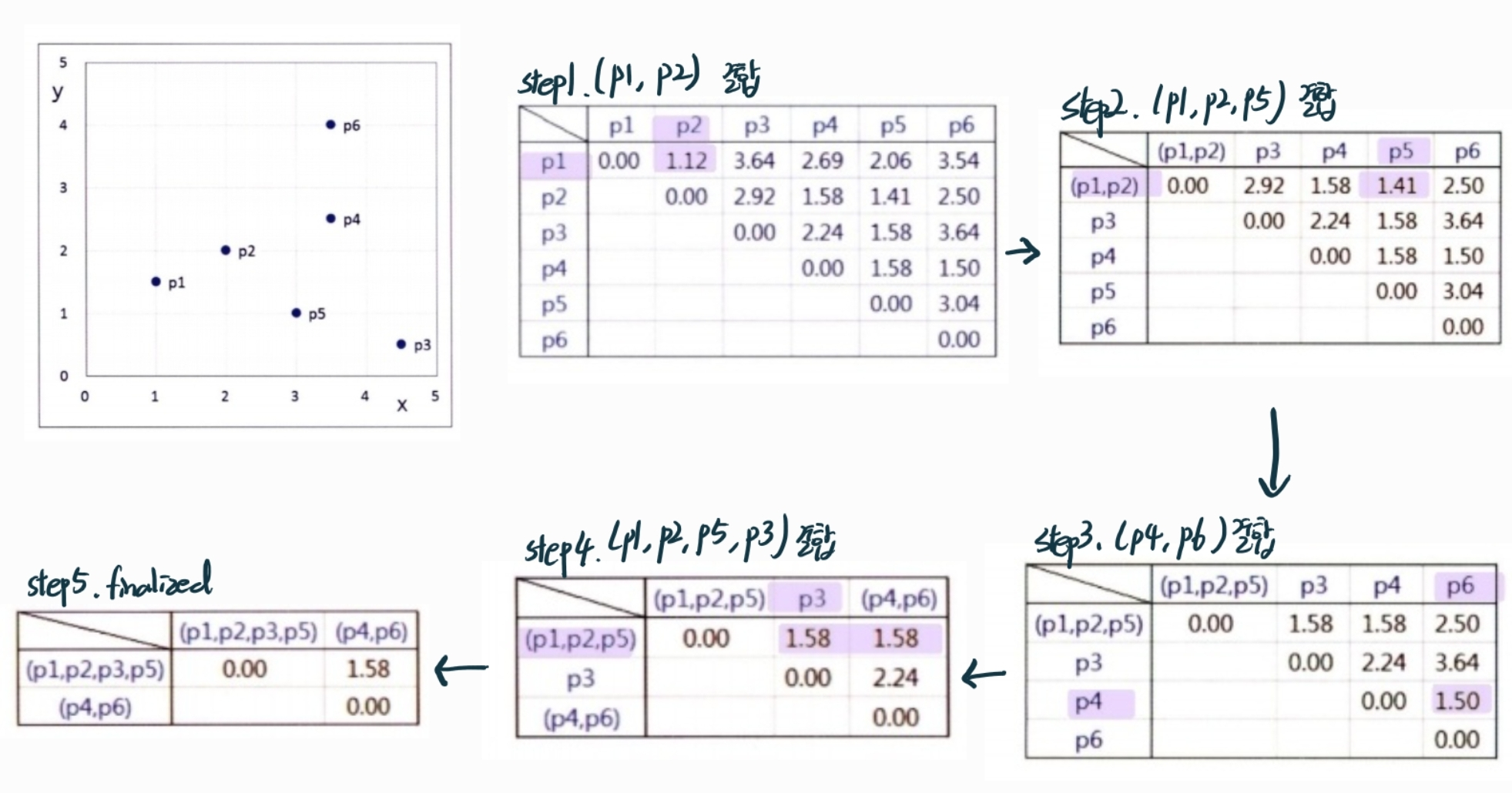
한 개의 레코드로 한 개의 군집을 구성하고, 군집간의 거리 행렬을 만든다.
거리가 가장 가까운 두 개의 군집을 한 개의 군집으로 합치고, 거리 행렬을 수정한다.
모든 레코드가 포함된 한 개의 군집이 만들어질 때까지 2단계를 반복한다.

병합적 클러스터링 장단점

장점
- 원하는 유사도와 연결법을 사용할 수 있어 다양한 공간에서 다양한 형태의 클러스터를 찾을 수 있음
- dendrogram을 이용하여 데이터에 따라 유연하게 최적의 클러스터 개수를 정할 수 있음
- 어떤 연결법을 사용하더라도 한 번에 하나씩 클러스터가 줄어들기 때문에 원하는 클러스터 개수를 찾을 수도 있음
단점
- K-means에 비하면 매우 느림 $O(n^3)$ 의 복잡도
  - 최장 연결법은 $O(n^2)$ 의 복잡도로 가장 효과적인 방법

병합적 클러스터링 기법들

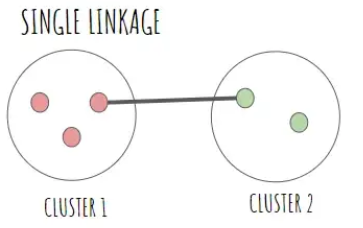
단일 연결법 (Single Linkage)

: 다른 군집에 속한 가장 가까운 두 점 사이의 거리를 군집 간의 거리로 측정하는 방법

$d(i+j, k) = min\{d(i,k), d(j,k)\}$
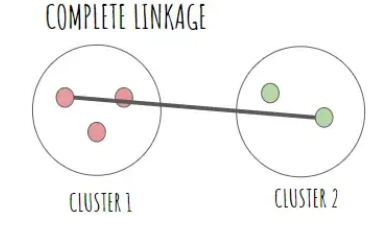
완전 연결법 (Complete Linkage)

: 다른 군집에 속한 가장 멀리 떨어진 두 점 간의 거리를 군집 간의 거리로 측정하는 방법

$d(i+j, k) = max\{d(i,k), d(j,k)\}$
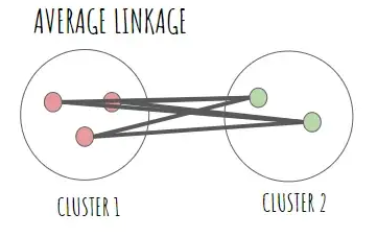
평균 연결법 (Average Linkage)

: 서로 다른 군집 간의 모든 짝을(pair-wise) 이룬 점들의 평균 거리로 유사성을 측정하는 방법

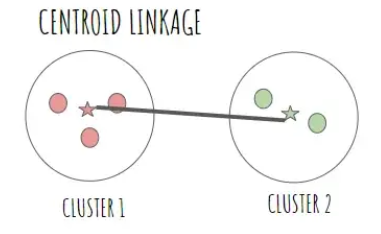
$d(C_1,C_2) = \frac{1}{n_in_j}\Sigma_{a\in C_i}\Sigma_{b\in C_j}d(a,b)$
중심 연결법 (Centroid Linkage)

: 두 군집 간의 거리를 측정할 때 각 군집의 중심(centroid) 간의 거리를 사용하는 방법

$d(i+j,k) = d(\mu_{i+j}, \mu_k)$

9-6-2. 분할적 클러스터링 (Divisive Clustering)

묶여있는 데이터를 나누어 점점 작은 군집을 만들어가는 알고리즘 (Top-down)
모든 관측치를 상호배타적으로 탐색하는 경우 O( $2^n)$ 의 복잡도
수행 단계
1. 모든 레코드가 포함된 한 개의 군집을 구성한다.
2. 만들어지는 군집 간의 거리가 최대가 되도록 두 개의 군집으로 분할한다.
3. 만들어진 군집들 중에 어느 것을 더 분할할 것인지 결정한다.
4. 한 개의 군집에 한 개의 레코드만 포함될 때까지 2,3단계를 반복한다.

9-6-3. 클러스터링 결과의 평가

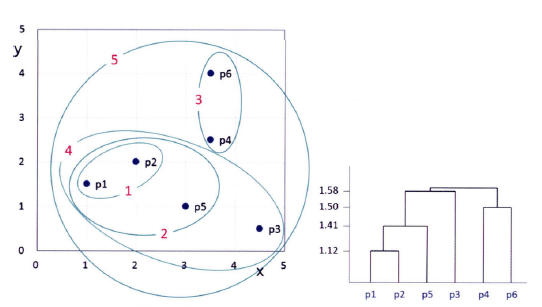
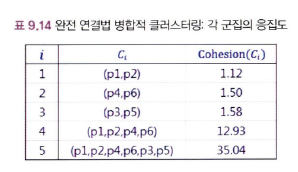
완전연결법의 결과를 통해 클러스터링 결과 평가 방법 설명

(p1,p2) → (p4,p6) → (p3,p5) → (p1,p2,p4,p6) → (p1,p2,p4,p6,p3,p5)의 순서로 군집이 만들어짐
각 군집의 응집도 계산

ex) $Cohension(C_4) = d(p1,p2) + d(p1,p4) + d(p1,p6) + d(p2,p4) + d(p2,p6)+d(p4,p6)$
군집의 개수에 따라 생기는 군집 및 응집도 합계

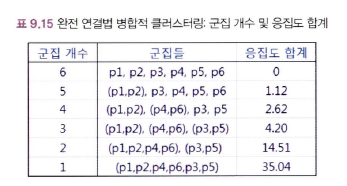
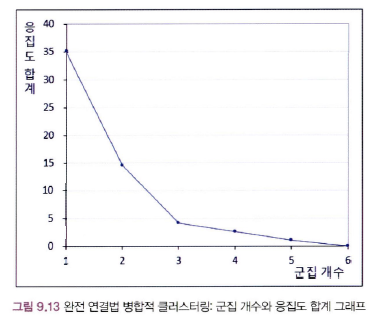
그래프의 기울기 변화가 급하다가 완만하게 변하는 지점(Elbow Point) → 군집개수=3

9-7. K-means clustering

: 가장 많이 사용하는 클러스터링 기법으로, 군집 중심점(centroid)이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법

군집 내 응집도 최대화 (maximizing cohesion within cluster) : 군집 내 중심과 해당 군집의 각 객체 간 거리의 합 최소화
군집 간 분리도 최대화 (maximizing separation between clusters) : 각 군집 중심 간 거리 합 최대화

이 두 목적함수를 만족하는 해 찾기

9-7-1. K-means clustering의 단계

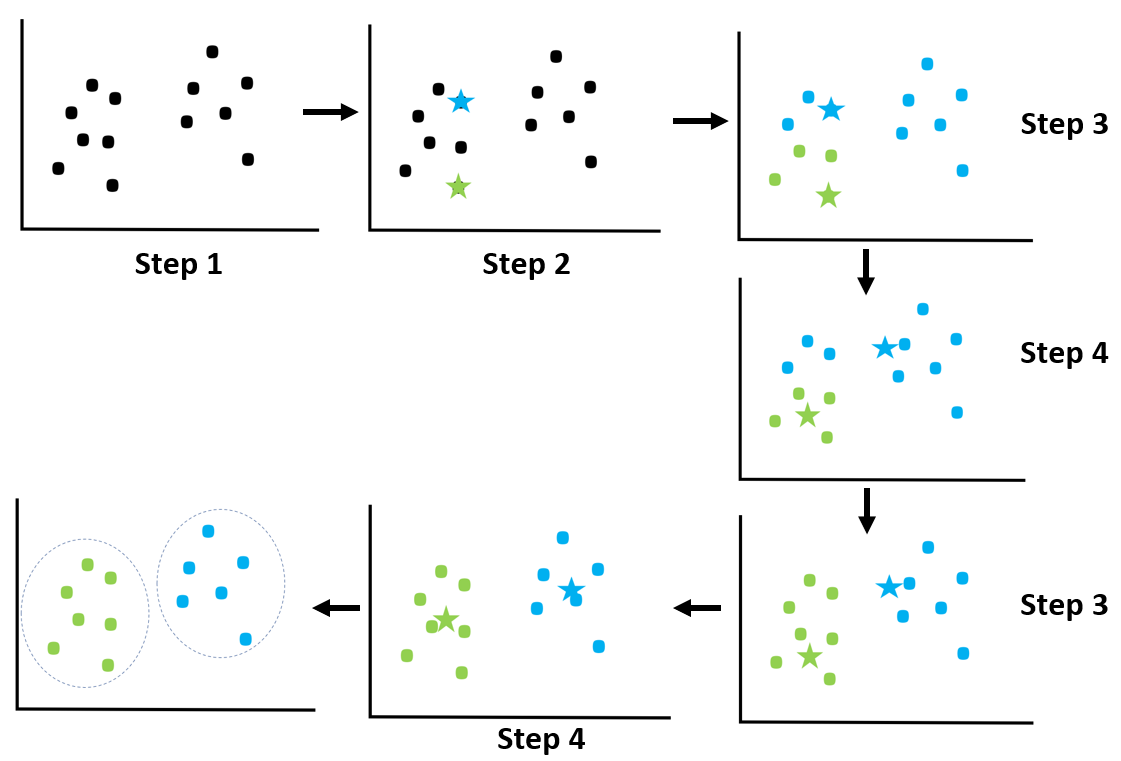
무작위로 K개의 레코드를 선택하여, 군집번호 1,…,K를 부여한다. 선택된 각 레코드가 각 군집의 중심이 된다.
각 레코드와 각 군집 중심 간의 거리를 구해서 가장 가까운 군집에 할당한다.
형성된 각 군집의 중심을 구한다.
각 군집에 속한 레코드의 변동이 없을 때까지 제 2, 3단계를 반복한다.

9-7-2. 초기 무작위 중심의 선택

처음 무작위 중심을 어떻게 고르냐에 따라 클러스터링 결과가 달라질 수 있다. → 초기 무작위 선택에 매우 민감
무작위 선택 Heuristic 방법
- 휴리스틱1
  
  첫 번째 무작위 중심은 무작위로 선택하고, 두 번째 무작위 중심은 첫 번째 무작위 중심과 가장 먼 레코드를 선택한다. 세 번째 무작위 중심은 첫 번째 및 두 번째 무작위 중심과 가장 먼 레코드를 선택한다.
- 휴리스틱2
  
  첫 번째 무작위 중심은 무작위로 선택하고, 두 번째 무작위 중심은 첫 번째 무작위 중심과 가장 가까운 레코드를 선택한다. 세 번째 무작위 중심은 첫 번째 및 두 번째 무작위 중심과 가장 가까운 레코드를 선택한다.

9-7-3. K-means clustering 장단점

장점
- 쉽고 간결한 알고리즘 → 해석이 용이
- O(nk)의 복잡도를 가져 속도가 빠름
- object function이 convex하기 때문에 무조건 수렴
단점
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우 군집화 정확도가 떨어짐 (이를 위해서 차원축소를 적용해야할 수도 있음)
- 반복을 수행하는데, 반복 횟수가 많을 경우 수행 시간이 매우 느려짐
- 몇 개의 군집을 선택해야할지 직접 선택해야함
- 처음 centroid를 어떻게 고르냐에 따라 성능이 많이 바뀜 → K-means++(2007)이 이 문제를 어느정도 개선
- 평균을 기준으로 하기에 이상치에 취약함

9-8. DBSCAN (Density Based Spatial Clustering of Applications with Noise)

: 정의한 밀도에 따라 인접한 데이터를 계속해서 묶어나가는 군집화 기법

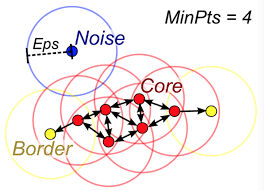
9-8-1. 수행과정

기준이 되는 거리값(Eps)와 최소한으로 포함되어야 하는 데이터 개수(MinPts)를 정의한다.
각 데이터를 기준으로 Eps 크기를 가지는 원을 그려서 그에 해당하는 데이터를 찾는다. 최소 데이터 개수(MinPts) 이상의 데이터가 포함되면 그 지점을 Core Point로 지정한다.
Core point와 연결된 모든 Core point들은 하나의 클러스터로 묶인다.
만약, 어떤 포인트가 2의 과정을 거쳤을 때 MinPts를 만족하지 못한다면 결과에 Core point가 포함되어 있는 경우에는 해당 지점은 Border Point가 된다. Border Point까지는 하나의 클러스터로 묶인다. 이런 방식으로 점차적으로 군집 영역을 확장한다.
Core point를 이웃 데이터로 가지지 않고 반경 내에 최소 데이터를 가지고 있지 않은 데이터는 잡음 데이터(Noise Point)로 판단한다.

9-8-2. DBSCAN 장단점

장점
- 다양한 형태의 데이터에 대해서 클러스터를 굉장히 잘 파악 (= 성능이 좋다.)
- 어떻게든 다른 클러스터에 모든 데이터를 포함시키는 다른 방법들과는 달리, outlier를 정의하고 있기 때문에 만들어진 클러스터의 품질이 좋음 (특징이 뚜렷하다, 밀도가 높다, 해석력이 뛰어나다)
단점
- MinPts와 Eps을 직접 선택해야함
- 모든 포인트에 Range Query를 계산해야 해서 꽤 느린 편 $O(N^2)$
- 고차원 공간에서 성능이 떨어짐 (Curse of Dimensionality)

9-9. 평균 이동 (Mean Shift)

: k-means과 유사하게 중심을 군집의 중심으로 지속적으로 움직이면서 군집화를 수행

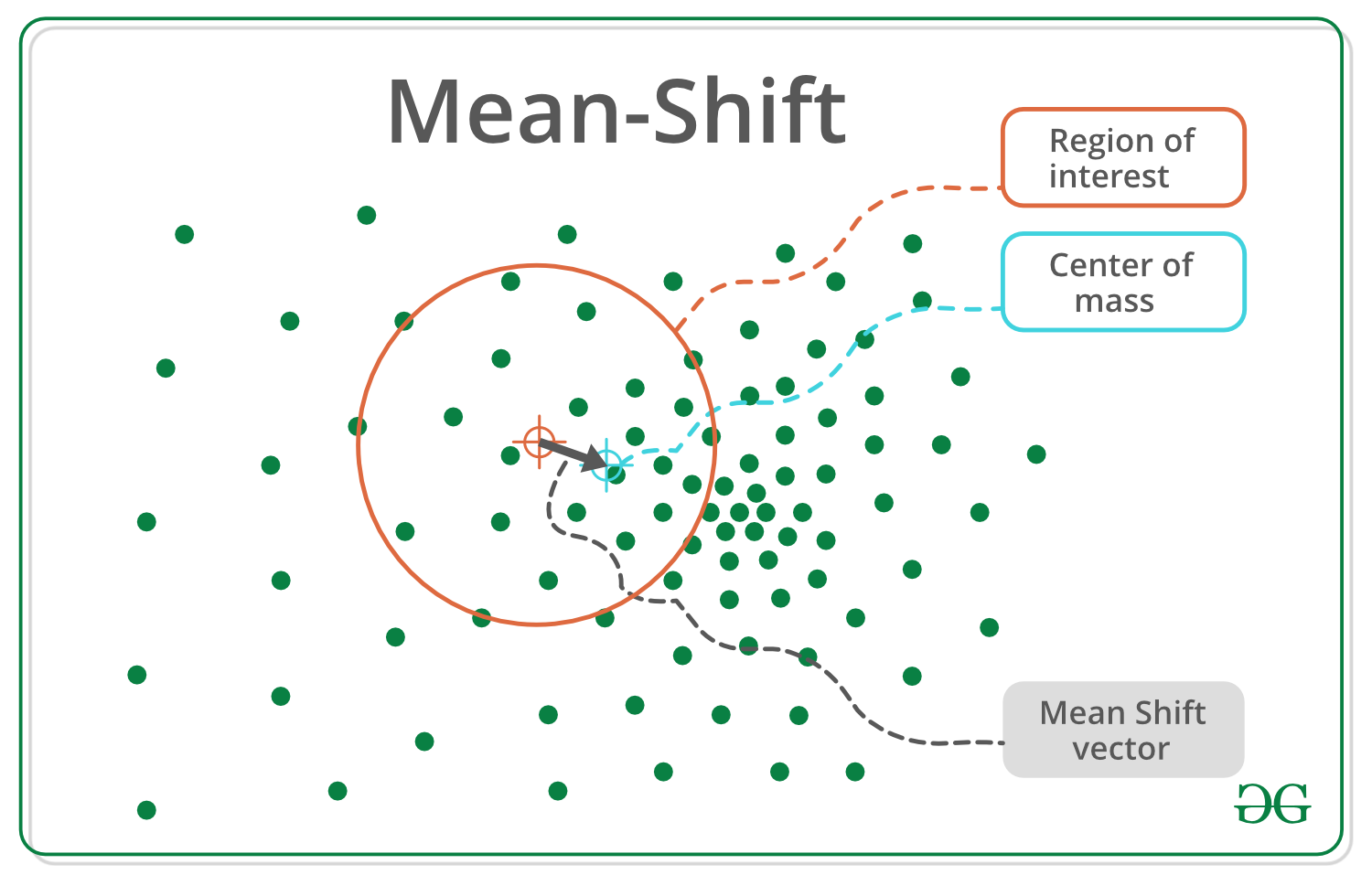
데이터가 모여 있는 밀도가 가장 높은 곳으로 이동
군집 중심점은 데이터 포인트가 모여 있는 곳이라는 생각에서 착안하여 probability density function (pdf)를 이용
분석 업무 기반의 데이터 세트보다는 컴퓨터 비전 영역에서 더 많이 사용

9-9-1. KDE (Kernel Density Estimation)

가장 집중적으로 데이터가 모여있어 확률 밀도 함수가 피크인 점을 군집 중심점으로 선정하며 일반적으로 주어진 모델의 확률 밀도 함수를 찾기 위해서 KDE(Kernel Density Estimation) 사용
KDE : 함수를 통해 어떤 변수의 확률 밀도 함수를 추정하는 방법

KDE=\frac{1}{n}\Sigma_{i=1}^{n} = \frac{1}{nh}\Sigma_{i=1}^nK(\frac{x-x_i}{h})

대역폭 h는 KDE 형태를 부드러운 형태로 평활화(smoothing)하는 데 적용되며, 이 h를 어떻게 설정을 하느냐에 따라 확률 밀도 추정 성능을 크게 좌우 가능
- h값 작음 → 좁고 뾰족한 KDE → 변동성이 크게 확률 밀도 함수를 추정 → over-fitting 되기 쉬움
- h값 큼 → 과도하게 평활화 되어 단순화된 방식으로 추정 → under-fitting되기 쉬움

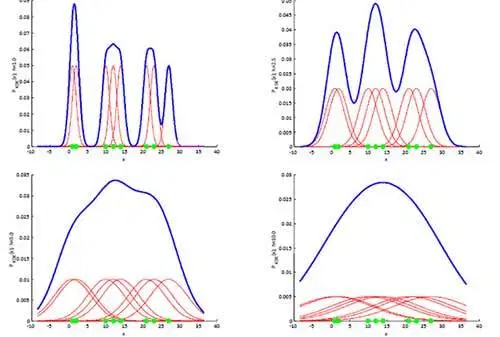
9-9-2. 평균 이동 수행 과정

개별 데이터의 특정 반경 내에 주변 데이터를 포함한 데이터 분포도를 KDE 기반의 Mean Shift 알고리즘으로 계산
KDE로 계산된 데이터 분포도가 높은 방향으로 데이터 이동
모든 데이를 1~1까지 수행하면서 데이터를 이동, 개별 데이터들이 군집중심점으로 모임.
지정된 반복(iteration) 횟수만큼 전체 데이터에 대해서 KDE 기반으로 데이터를 이동시키면서 군집화 수행
개별 데이터들이 모인 중심점을 군집 중심점으로 설정

9-9-3. 평균 이동 장단점

장점
- 좀 더 유연한 군집화가 가능 (데이터 세트의 형태를 특정 형태로 가정 or 특정 분포도 기반의 모델로 가정하지 않기 때문)
- 이상치의 영향력 크지 않음
- 미리 군집의 개수를 정할 필요 없음
단점
- 수행 시간이 오래 걸림 $O(n^2)$
- hyperparameter (band-width)의 크기에 따른 군집화 영향 큼

9-10. GMM (Gaussian Mixture Model)

: 데이터가 여러 개의 가우시안 분포를 가진 데이터 집합들이 섞여서 생성된 것이라는 가정하에 군집화를 수행하는 방식

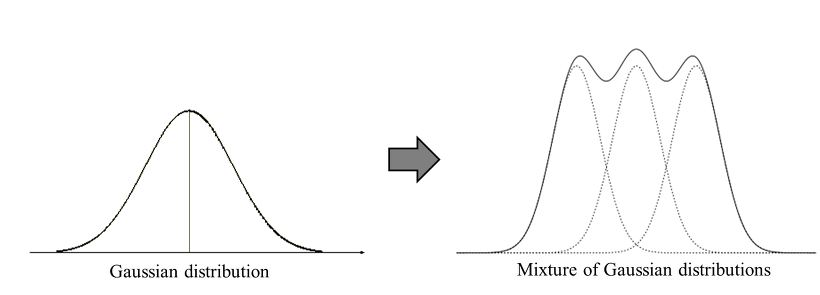
GMM은 데이터를 여러 개의 가우시안 분포가 섞인 것으로 간주하고 섞인 데이터 분포에서 개별 유형의 가우시안 분포 추출
GMM의 모수 추정
- 개별 정규 분포의 평균과 분산
- 각 데이터가 어떤 정규 분포에 해당되는지의 확률
  
  모수추정은 이 2가지를 추정것

9-10-1. GMM 수행 단계

예측(Expectation)과 최대화(Maximization)의 2단계를 통한 모수 추정

예측 (Expectation) : 개별 데이터 포인트가 각 정규 분포로부터 생성되었을 가능도(likelihood)를 계산하여, 가장 높은 확률을 가진 정규 분포에 할당

ex)

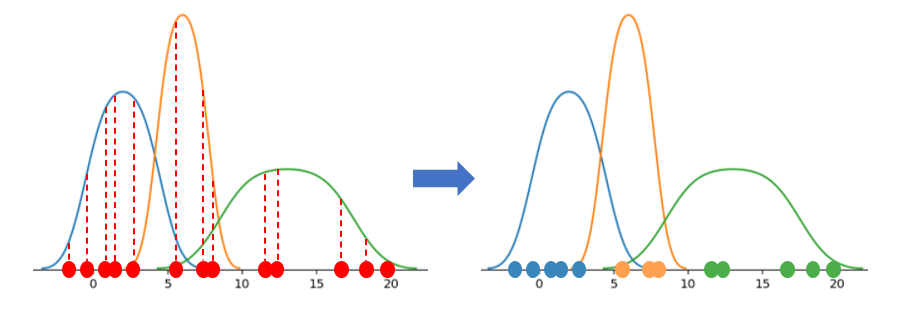
위 그림처럼 빨간 색으로 표시된 각 데이터 포인트에 대해 각 정규 분포에 속할 확률을 계산한 후, 가장 큰 확률을 갖는 정규 분포로 할당한다. 파란색 정규 분포에 5개의 데이터 포인트가, 주황색 정규 분포에 3개의 데이터 포인트가, 초록색 정규 분포에 5개의 데이터 포인트가 할당되는 것을 확인할 수 있다.
최대화 (Maximization) : 위 1번 단계에서 개별 데이터 포인트를 모두 할당한 후, 각 그룹의 데이터 포인트를 이용하여 Maximum Likelihood Estimation(최대 우도 추정)으로 모분포의 모평균과 모분산을 추정

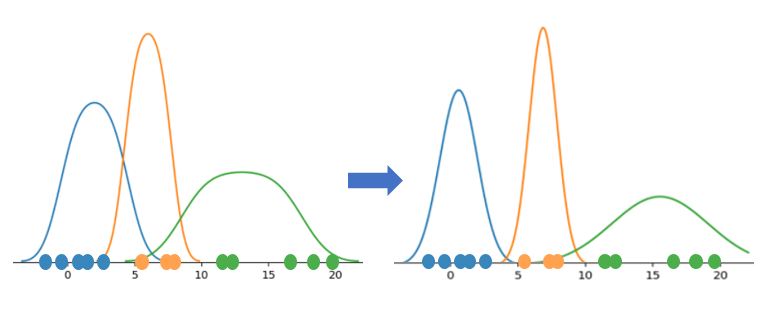
개별 데이터 포인트로 각 정규 분포의 모수를 추정한다. 위 그림에서 정규 분포의 평균과 분산이 변경된 것을 확인할 수 있다. 개별 데이터들의 소속과 정규 분포의 모수(평균과 분산)가 변하지 않을 때까지 1,2 단계를 반복 수행한다.

9-10-2. GMM 장단점

장점
- 데이터가 기하학적 모양의 군집을 갖는 경우, K-means 알고리즘보다 성능이 좋다
- Mixture Model 중에서는 학습 속도가 빠른 편이다.
- 유연하게 다양한 데이터 세트에서 잘 적용 가능
단점
- 군집의 개수를 의미하는 가우시안 분포의 개수를 사용자가 지정
- 계산량이 많은편이어서 수행 시간이 오래 걸림
- 가우시안 분포마다 충분한 데이터 포인트들이 있어야 모수 추정이 잘 이뤄짐

Reference

[1] 데이터 애널리틱스 (이재식, 2020)

[2] https://www.researchgate.net/figure/A-broad-classification-of-the-most-common-clustering-methods-Barnard-and-Downs-2002_fig1_255656001

[3] https://towardsdatascience.com/17-clustering-algorithms-used-in-data-science-mining-49dbfa5bf69a#8925

[4] R분석과 프로그래밍

[5] 파이썬 머신러닝 완벽 가이드 (권철민, 2021)

[6] https://cmparlettpelleriti.github.io/CohandSep.html

[7] Google Developers Machine Learning 고급과정 클러스터링

[8] https://levelup.gitconnected.com/evaluating-socio-economical-indicators-with-exploratory-analysis-and-hierarchical-clustering-af1575782141

[9] https://tyami.github.io/machine learning/clustering/

[10] https://www.geeksforgeeks.org/ml-mean-shift-clustering/

[11] https://studying-haeung.tistory.com/14