[ML] 머신러닝 평가지표 - 회귀, 분류, 클러스터링

youngchae·2022년 9월 2일

머신러닝 분류 클러스터링 평가지표 혼동행렬 회귀

ML

목록 보기

3/5

Q. 알고 있는 metric에 대해 설명해주세요. (ex. RMSE, MAE, recall, precision ...)

1. 회귀 모델 평가 지표

MAE, MSE, RMSE, MSLE, MAPE, MPE, R^2

MAE(Mean Absolute Error)
- 실제 값과 예측 값의 차이를 절대값으로 변환해 평균화
- 에러에 따른 손실이 선형적으로 올라갈 때 적합
  $MAE = {\frac{1}{N}\sum_{i=1}^{N}{|yi-\hat{yi}}|}$
MSE(Mean Squared Error)
- 예측값과 실제값 차이의 면적의 합
- 특이값이 존재하면 수치가 많이 늘어남
  $RMSE = {\frac{1}{N}\sum_{i=1}^{N}{(yi-\hat{yi}})^2}$
RMSE(Root Mean Square Error)
- MSE에 루트를 씌운 값
- 에러에 따른 손실이 기하 급수적으로 올라가는 상황에서 쓰기 적합

RMSE = \sqrt{\frac{1}{N}\sum_{i=1}^{N}{(yi-\hat{yi}})^2}

MSLE(Mean Squared Log Error)
- MSE에 로그 적용
  $MSLE = {\frac{1}{N}\sum_{i=1}^{N}{(log(yi+1)-log(\hat{yi}+1)})^2}$
MAPE(Mean Absolute Percentage Error)
- MAE를 퍼센트로 변환
  $MAPE = \frac{1}{N}\sum_{i=1}^{N}{\frac{|yi-\hat{yi}|}{yi}}*100$
MPE(Mean Percentage Error)
- MAPE에서 절대값을 제외한 지표
  $MPE = \frac{1}{N}\sum_{i=1}^{N}{\frac{yi-\hat{yi}}{yi}}*100$
R Squared(결정계수)

R^2 = \frac{SSE}{SST}=1-\frac{SSR}{SST}

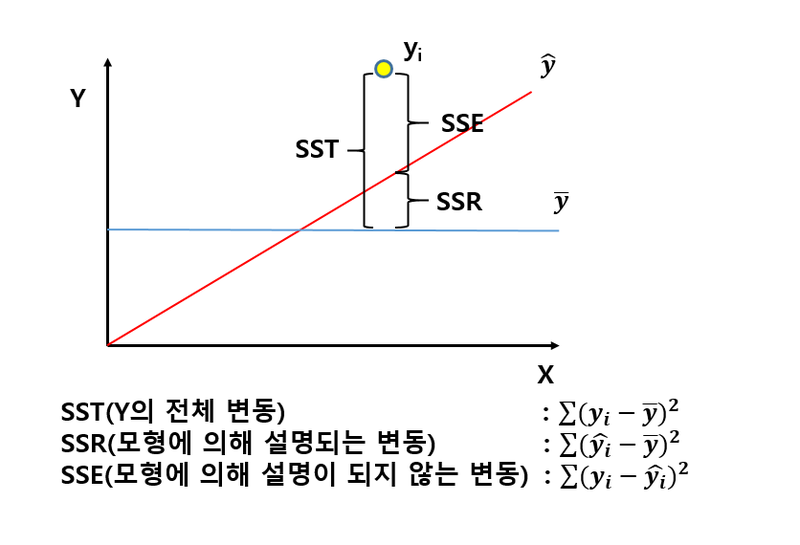
Adjusted R Square
- 독립변수의 개수가 증가하면 결정계수는 일방적으로 증가
  Adjusted R^2는 분자를 감소시켜주는 연산을 통해서 일방적인 증가를 방지

Adjusted R^2 = 1=\frac{SSR/(n-k-1)}{SST/(n-1)}

2. 분류 모델 평가 지표

Accuracy, Precision, Recall, F1-score, ROC-AUC

Confusion Matrix (혼동행렬)의 이해

Type1 error = α error= FP
: 실제로 귀무가설이 참이지만, 귀무가설을 기각하는 오류
: 참이라고 잘못 예측 → 대체적으로 더 심각한 에러
Type2 error = β error= FN
: 실제로 귀무가설이 거짓이지만, 귀무가설을 채택하는 오류
: 거짓이라고 잘못 예측

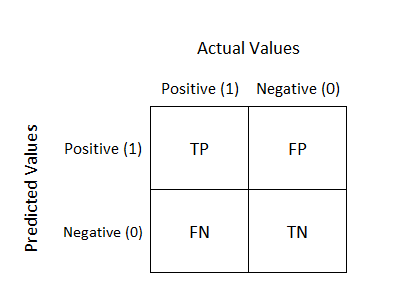
분류 모델 평가 지표

Accuracy(정확도)
- 전체 데이터 중에서 올바르게 예측한 비율
- 데이터가 imbalance한 경우 정확도는 성능을 측정하는 데 좋은 지표가 되지 못함

Accuracy = \frac{TP+TN}{TP+TN+FP+FN}

Precision(정밀도)
- 모델이 true로 분류한 것 중에서 실제로 true인 것의 비율
- 거짓 양성(FP)으로 판단하지 않는 것이 중요한 경우
  
  ex) 스팸 메일 분류기

Precision = \frac{TP}{TP+FP}

Sensitivity(민감도)= Recall(재현율) = TPR
- 실제로 true인 것들 중에서 예측이 true인 것의 비율
- 거짓 음성(FN)으로 판단하지 않는 것이 중요한 경우
- 실제로 질병이 있을 때, 질병이 있다고 예측할 확률
  
  ex) 암 진단
  $Recall = \frac{TP}{TP+FN}$
Specificity(특이도)
- 실제로 false인 것들 중에서 예측이 false인 것의 비율
- 실제로 질병이 없을 때, 질병이 없다고 예측할 확률
  $Specificity = \frac{TN}{TN+FP}$
F1-score
- Precision과 recall의 조화평균
  $F1-score = \frac{1}{\frac{1}{precision}+\frac{1}{recall}} = \frac{2*precision*recall}{precision+recall}$ ❓ precision과 recall의 산술평균을 사용하지 않고 조화평균을 사용하는 이유
  precision과 recall은 하나가 높아지면 하나가 낮아지는 관계 (trade-off 관계)
  둘 중 하나가 0에 가깝게 낮을 때 지표에 그것이 잘 반영되게 하기 위해서 (두 지표 모두 균형있게 반영하기 위해)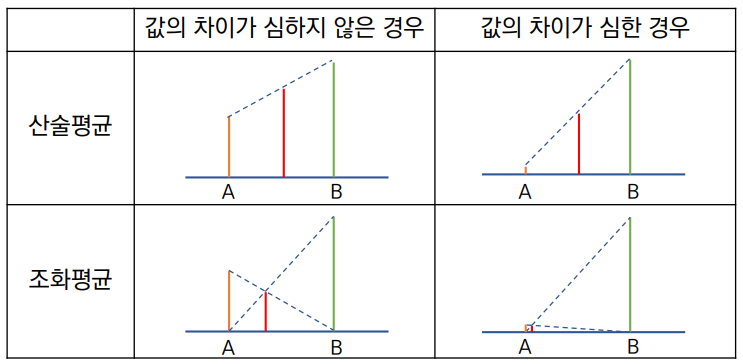
MCC(Matthew’s correlation coefficient)
- 이진 분류에 사용되는 지표로, 불균형한 데이터의 모델 성능을 적절하게 평가하기 쉬운 지표
- -1과 1 사이의 값을 가짐
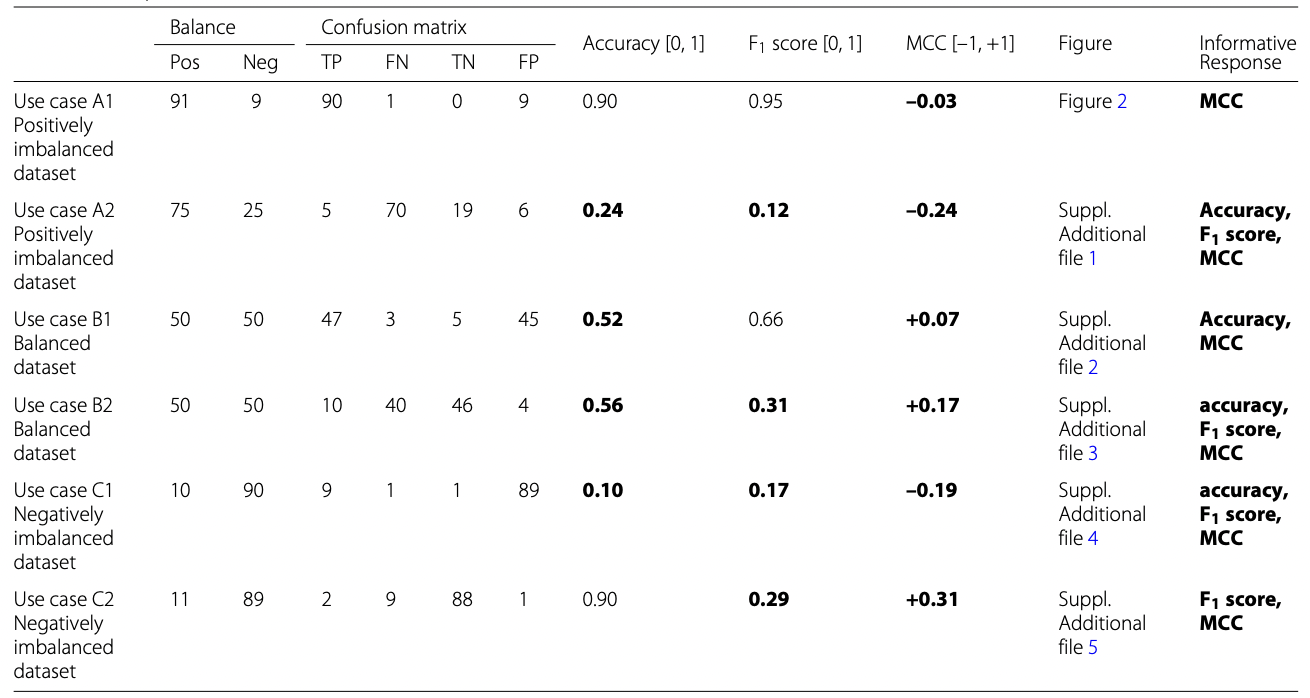
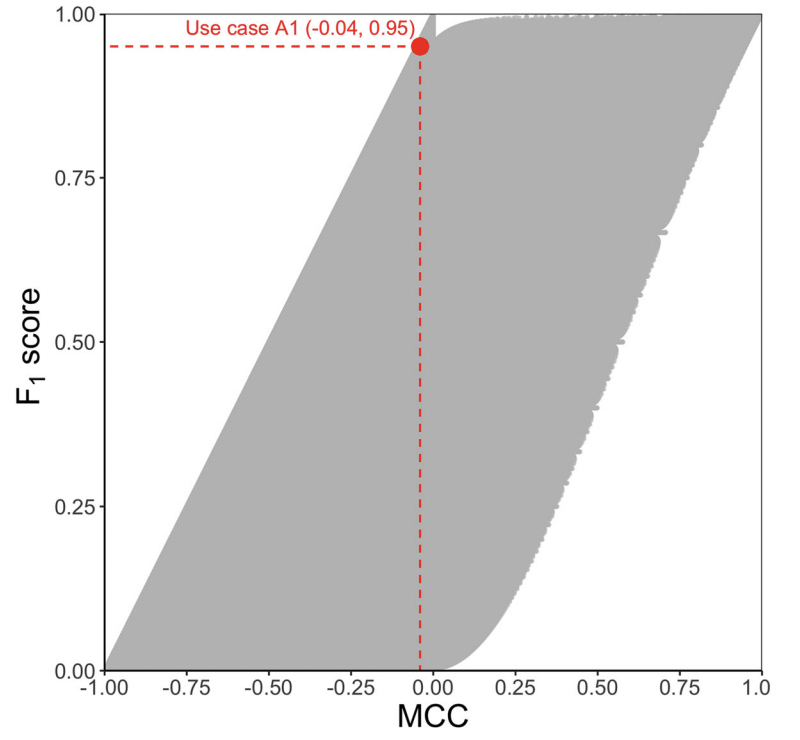
  $MCC = \frac{TP*TN-FP*FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$
- 이 표에서 첫번째와 같은 데이터일 때 다른 어떤 지표보다 MCC를 사용하는 것이 효과적
  - 긍정으로 치우친 데이터이면서, 0인 데이터 중 맞춘 데이터(TN)가 적을 때
- Matthew’s correlation coefficient와 F1-score의 차이점
  1. f1-score는 부정으로 올바르게 분류된(TN) 샘플의 수로부터 독립적
  2. f1-score는 class가 달라짐에따라 달라짐, MCC는 긍정 클래스의 이름이 부정으로 바뀌어도 불변
    
    → MCC가 f1-score보다 완벽한 지표라고 이야기들 함
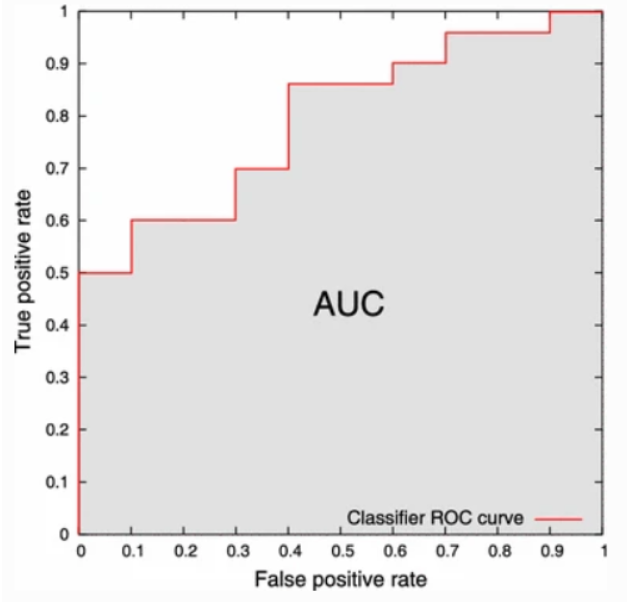
AUC(Area Under the Cover)-ROC(Receiver Operating Characteristic)
- ROC : FPR이 변화할 때, TPR이 어떻게 변화하는지 보여주는 곡선
  - threshold(임계값)에 따른 이진분류기의 성능을 한번에 볼 수 있음
- AUC : ROC 아래의 넓이
- x축 :FPR=1-specificity, y축:TPR=sensitivity
- 우수한 모델일수록 AUC 값이 1에 가까움, ROC curve가 좌상단에 붙어있음

3. 클러스터링 모델 평가지표

Silhouette coefficient (실루엣 계수)
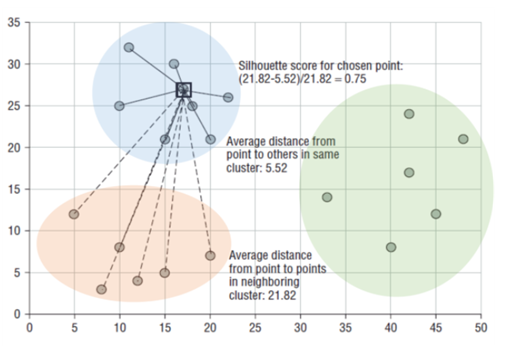
- 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집화 되어 있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리되어 있는지를 나타내는 지표
- -1 ~ 1 사이의 값을 가짐
- 1로 가까워 질수록 근처의 군집과 멀리 있음, 0에 가까울수록 근처의 군집과 가까움 (1에 가까울수록 클러스터링이 잘 된 것이라고 말 할 수 있음)
- 전체 실루엣 계수의 평균값과 더불어 개별 군집의 평균값의 편차가 크지 않아야 좋은 군집화라고 할 수 있음