Abstract
본 연구에서는 주기성을 이용하여 LTSF 태스크에서 좋은 성능을 보이는것을 목표로 한다. 구체적으로 Residual Cycle Forecasting (RCF)라는 학습가능한 recurrent cycles를 활용해서 내제적 주기 패턴을 모델링하고, 사이클의 남은 컴포넌트에 대해 예측을 수행한다. RCF을 리니어 레이어 MLP를 혼합함으로써 파워풀한 성능을 보인다. CycleNet은 SOTA 성능을 달성하였고, 90%의 파라미터 양을 줄였다. 게다가 플러그 앤 플레이 테크닉을 통해서 RCF는 기존 모델의 PatchTST 와 iTransformer의 예측 정확도를 향상시켰다.
1 Introduction
RNN 기반 모델들은 롱텀의 의존도를 효과적으로 모델링 할 수 있고, 정확하게 주기적 패턴을 인지하여 롱텀 예측을 할 수 있다. 그러나, 이러한 딥하고 복잡한 모델들은 단지 넓은 길이의 의존도를 주기적으로 추출하기 위한 것이다. 패턴을 직접적으로 모델링하면 되지 않을까?
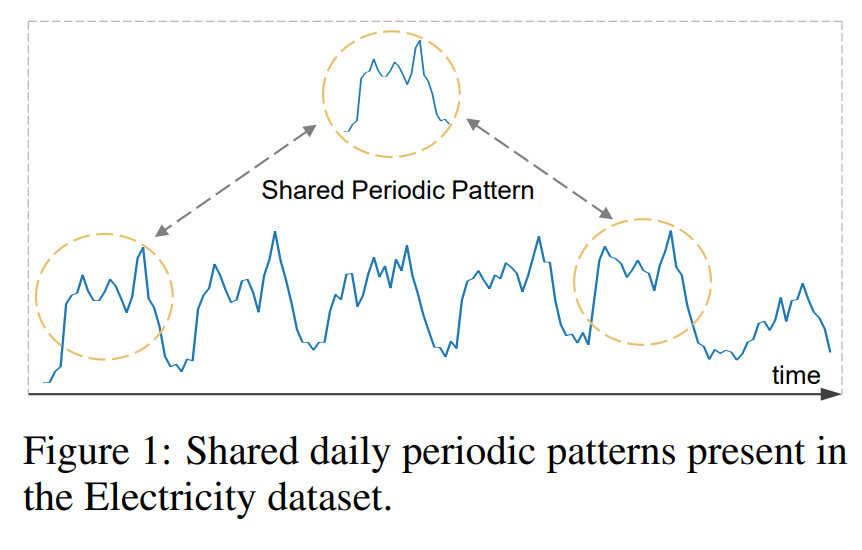
Fig 1. 에서 전기 데이터는 데일리한 주기적 패턴을 보인다. 글로벌하게 공유된 데일리 segment를 공유하며, 이를 주기적으로 N 타임 반복함으로써 지속적으로 사이클릭 컴포넌트에 대한 표현을 나타낼 수 있다.
이러한 모티베이션으로부터, LSTF 태스크에서 이러한 주기 패턴을 활용하여 RCF(Residual Cycle Forecasting) 을 제안한다. Learnable recurrent cycle을 사용하며 명시적으로 모델링을 하게 되는데, 또한 얕은 MLP를 통해 residual component를 예측하여 이 둘을 합침으로써 CycleNet이라고 한다. CycleNet은 간단하지만 효과적이며, SOTA퍼포먼스를 보인다. Contribution은 다음과 같다.
1. 공유된 periodic 패턴을 인지하고, 이를 명시적으로 모델링하여서 모델의 LSTF 태스크에서의 성능을 향상시킨다.
2. RCF 테크닉을 제안하여 learnable recurrent cycle을 통해서 시계열에 내재된 주기정보를 학습하고, residual 컴포넌트를 예측한다. RCF는 기본 모델대비 성능을 향상시킨다.
3. MLP를 통해 RCF를 설계하면서, CycleNet은 SOTA를 달성한다.
2 Related work
주기 정보를 활용하여서 모델의 예측 성능을 높이는 것은 독창적인것은 아니다. 다양한 시즈널과 트랜드 분해를 통해서 (STD) 연구들이 있어왔는데, 유명한 모델은 Autoformer, FEDformer, DLinear 등등이 있다. 이들은 시즈널과 트랜드를 분해하고, 각각 모델링한다는 특징이 있다. STD 방법론들은 moving average 커널을 통해서 트랜드 컴포넌트를 얻는다. 최근에 Leddam 은 MOV 커널을 Learnable Decomposition kernel로 대체하였다. 또한 DEPTS는 주기성을 시간에 파라미터화된 함수로 보아 주기와 residual 컴포넌트들을 레이어 와이즈 하게 학습하였다. SpareseTSF는 크로스 주기 sparse 예측 테크닉을 통해서 사이클과 트랜드를 디커플하였고, 낮은 비용으로 좋은 성능을 내었다.
본 연구의 RCF 테크닉은 STD의 하나의 타입이라고 간주된다. 하지만 기존 연구들과 다른 점은, global로 공유되는 주기 패턴에 대해서 learnable recurrent cycle을 통해 명시적으로 모델링 하였다는 점이다. 제안된 RCF 테크닉은 컨셉적으로 심플하지만 효과적이며 예측 정확도가 높다.
3 CycleNet
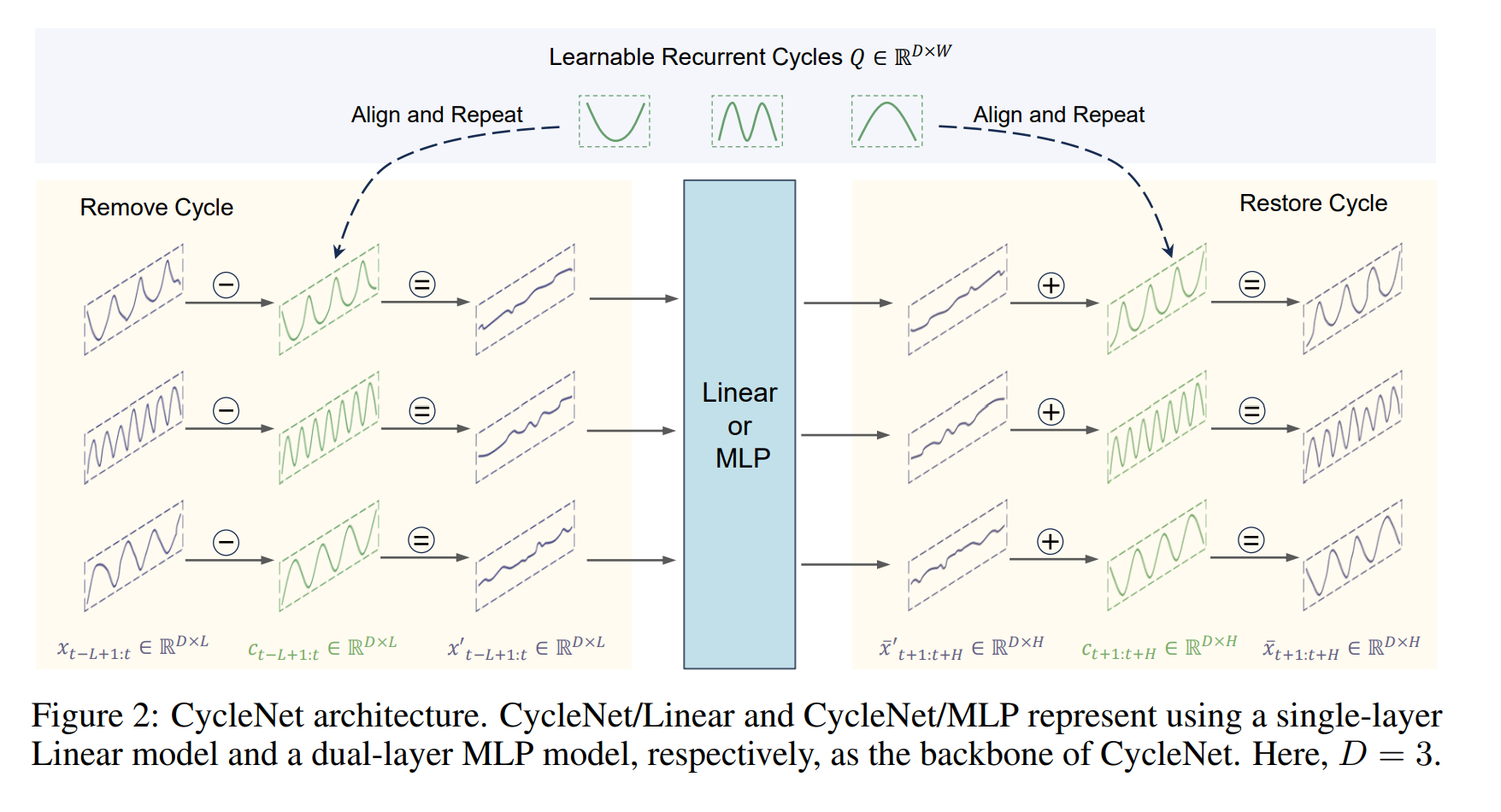
X 시계열에 대해서 D 변수 혹은 채널이 있다고 한다면, 시계열 예측의 목적은 H step 에 대한 예측을 이전 L 의 관측에서 수행하는 것이다. 시계열에 내재된 주기를 통해 롱텀 (96~760)을 예측할 때 모델의 퍼포먼스를 향상시키기 위해서 Residual Cycle Forecasting 테크닉을 활용한다.
3.1 Residual cycle forecasting
Periodic patterns modeling
D 채널이 있을 때, cycle 길이 W가 있다고 하면, 러너블 recurrent 사이클을 모아 Q 로 정의하고, 모두 0으로 초기화된다. 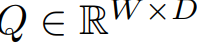
이 사이클들은 채널 안에서 글로벌하게 공유되며, 사이클 replications를 수행하여서 cyclic 컴포넌트 C들을 sequence 길이 X로 얻는다. 이러한 recurrent 사이클 Q는 W의 길이를 가졌으며, backprop을 거쳐서 학습을 수행한다. 학습된 표현은 시퀀스 내의 사이클릭 패턴들을 나타낸다.
사이클 길이 W는 데이터셋의 특성에 의존하며, 데이터셋에서 가장 안정적인 사이클에 맞춰야 한다. 롱텀예측을 요구하는 태스크에서는 대게 prominent하고 명확한 사이클들을 요구하고, 특정 사이클 길이가 필요하다. 이러한 데이터셋의 사이클들은 ACF 를 통해 측정이 가능하다.
Residual forecasting
모델된 사이클들의 residual components 에 대해서 residual forecasting이라고 하며, 다음과 같다.
1. 오리지널 인풋에서 사이클릭 컴포넌트를 제거한것이 residual component 이다.
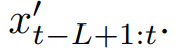
2. 백본 모델에 이를 통과시켜서 residual component에 대한 예측을 수행한다.
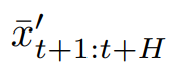
3. 예측 결과를 주기 컴포넌트에 추가하여서 최종 예측 결과를 얻는다.
cyclic 컴포넌트 C는 가상의 시퀀스로, Q의 레틀리케이션이다. 언급한 서브 시퀀스들은 은 직접 업을 수 없기 떄문에 Fig 3. 와 같이 적절한 alignment와 repetition 을 통해 만든다.
이는 1) left shift 2) Repeat Q 가 있다. 이러한 2개의 서브시퀀스들은 다음과 같이 표현된다.
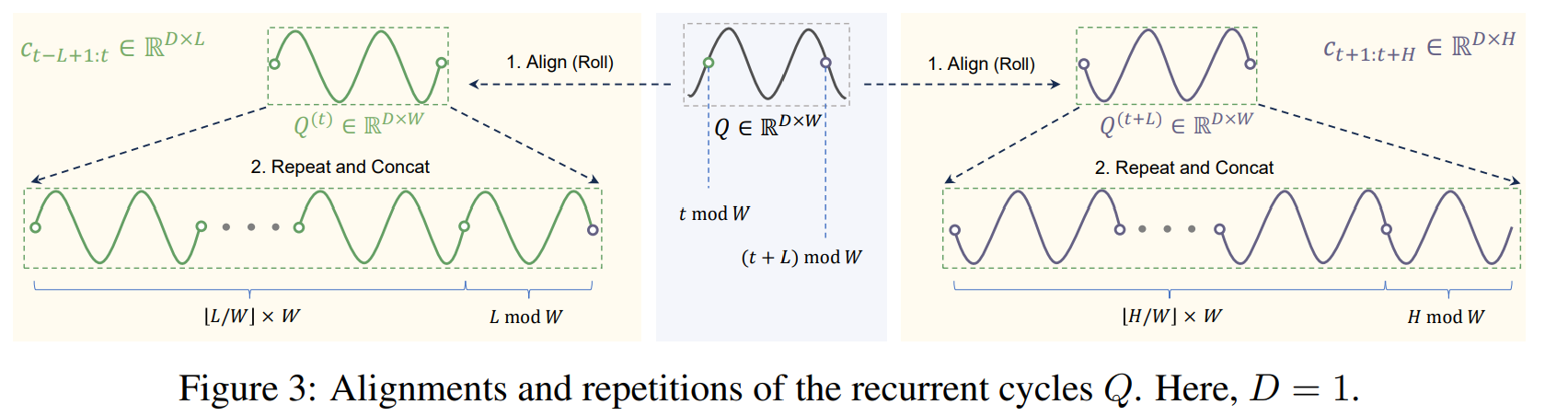
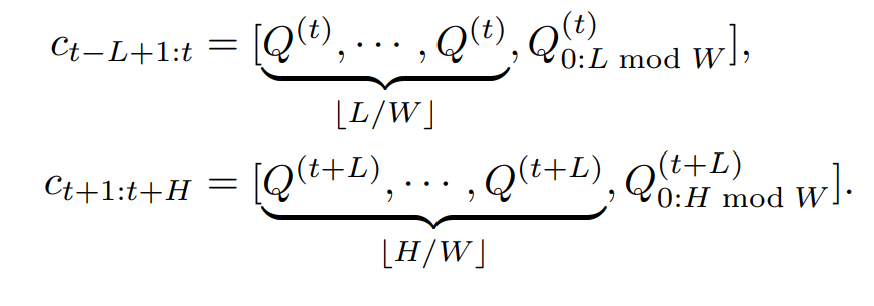
Backbone
오리지널 예측 태스크는 사이클릭 residual 컴포넌트 모델링으로 변환이 되며, 노멀 시퀀스 모델링이 된다. 그러므로, 존재하는 시계열 예측 모델이 백본으로 사용된다. 본 연구에서는 시계열 예측을 향상시키는 방법으로 RCF를 통해 사이클을 명백히 모델링한다. 그러므로, 대부분의 기본 백본에 싱글 및 듀얼 MLP 레이어를 사용함으로써, CycleNet/Linear and CycleNet/MLP를 제안한다. 각 채널은 같은 백본으로 파라미터를 공유하면서 모델링을 수행한다.
3.2 Instance normalization
시계열 데이터는 평균과 분산이 바뀌는 경우가 있다. 이는 분포 변화를 의미하며, 모델이 이전 학습 데이터에서 미래 데이터를 예측하는데 퍼포먼스를 낮추는 원인이 된다. 따라서 이러한 이슈를 다루기 위해서 Insatance Normalization RevIN 과 같은 연구들이 있었는데, 이와 비슷하게 CycleNet 모델 내부에서 변하는 통계 특성을 다루지 않게 다음과 같이 사용하여 처리한다.
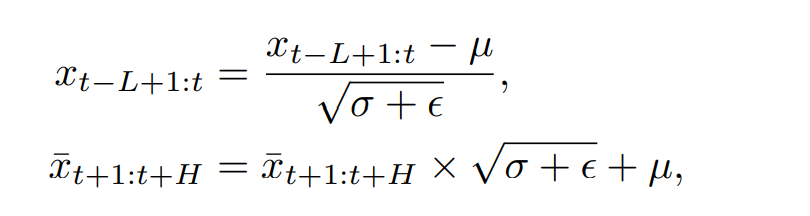
3.3 Loss function
다음과 같이 MSE 로스를 사용한다.
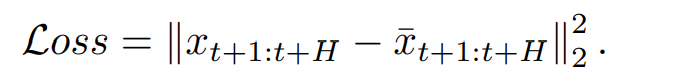
4 Experiments
4.1 Setup
Datasets
ETTh1 & ETTh2 ETTm1 & ETTm2 Electricity Solar-Energy Traffic Weather를 사용한다.
Baselines
iTransformer, PatchTST , Crossformer, TiDE, TimesNet, DLinear, SCINet, FEDformer, Autoformer 가 있다.
Environments
VIDIA GeForce RTX 4090 GPU 를 사용하였다.
4.2 Main results
CycleNet/MLP 는 다변량 LSTF 태스크에서 SOTA 성능을 나타내었다. RCF 테크닉을 추가함으로써 기본적인 MLP와 Linear 모델도 SOTA를 달성할 수 있었다.
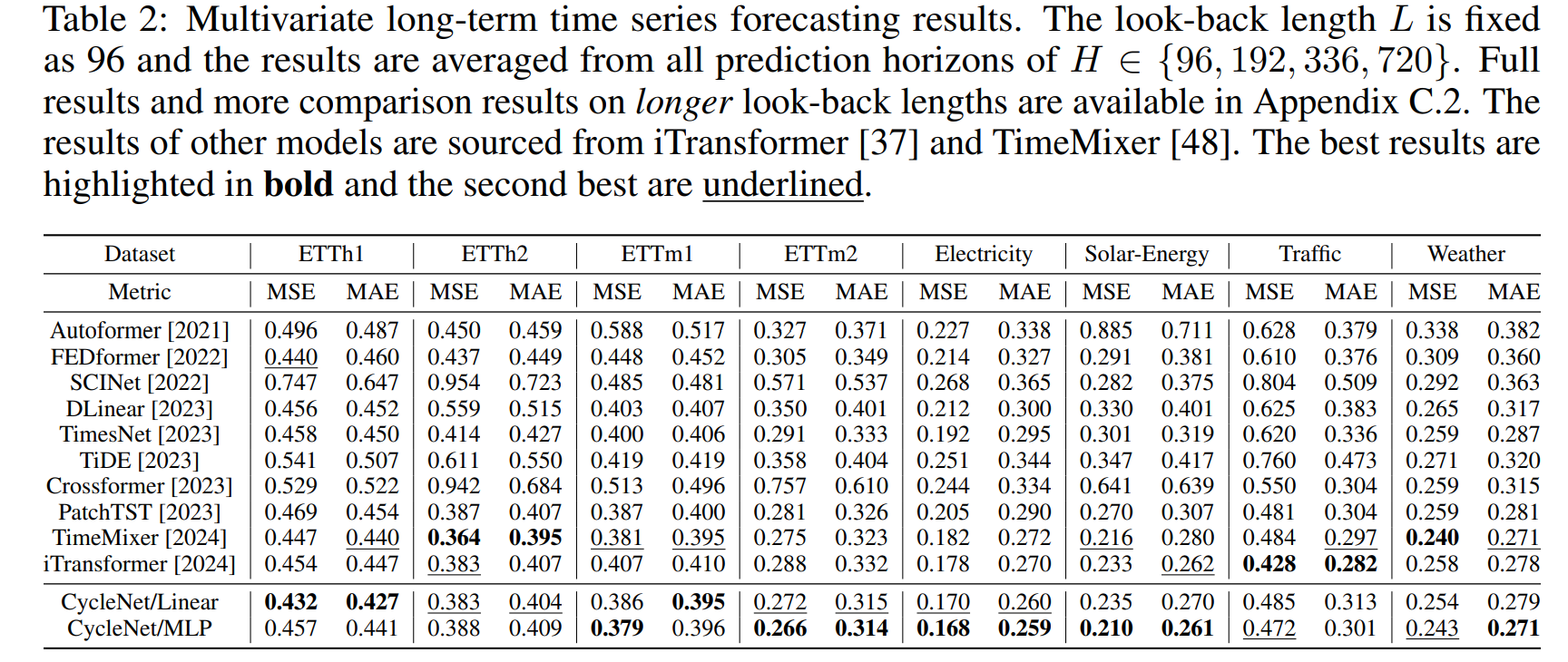
또한, Traffic 데이터셋에서 CycleNet의 퍼포먼스가 iTransformer 에 비해 뒤쳐지는데, 이것은 시계열의 다변수의 관계를 모델링하는 트랜스포머가 유리했기 때문이다. 이는 Traffic 데이터가 공간시간적 특성을 가지고, lag를 가지는 특성을 가지며, 트래픽 흐름이 특정 포인트에서 다른 포인트로 넘어가는 성질이 있기 때문이다. 이러한 케이스에서는 inter-channel 관계를 모델링하는것이 필수인데, CycleNet은 각 채널의 temporal 의존도를 다루지 않기 떄문에 이러한 경우에는 성능이 낮게 나왔다. 하지만 다른 데이터셋에서는 좋은 성능을 보였다.
4.3 Efficiency analysis
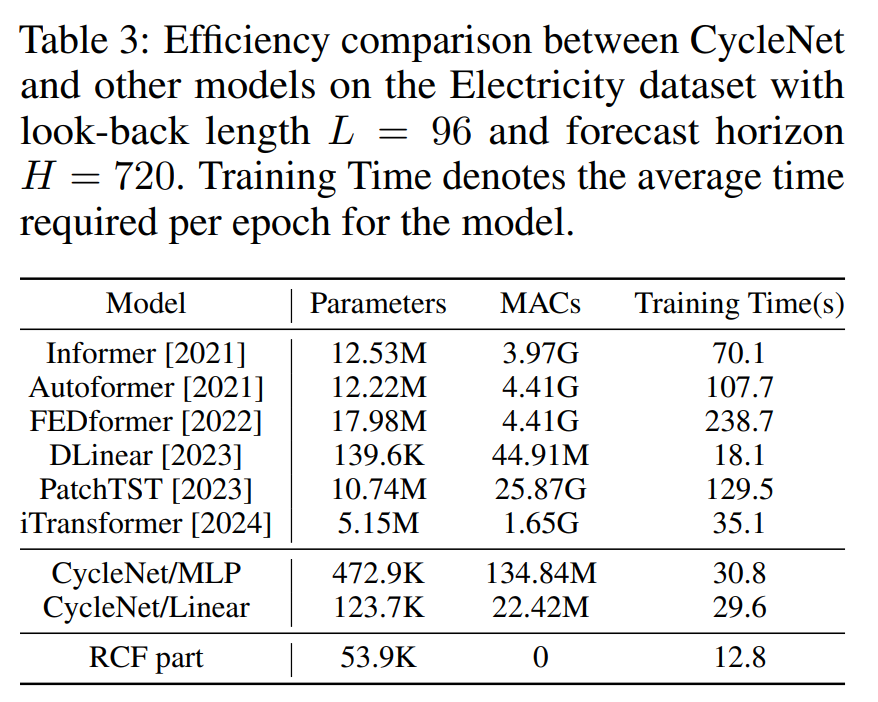
TCF 테크닉은 플러그앤 플레이 모듈이기 때문에 Multiply-Accumulate
Operations (MACs)을 추가하지 않는다. 사이클넷의 백본은 MLP 혹은 Linear 이므로, 아주 낮은 복잡도를 가지낟. RCF 는 단지 DLinear 보다 학습 시간이 더 걸린다. 이는 RCF 테크닉은 각 데이터 샘플의 recurrent 사이클들에 대해 정렬하는 과정이 필요하기 때문에 CPU 타임을 필요로 한다. 하지만, 퍼모먼스와 효율의 최고의 밸런스를 보여준다.
4.4 Ablation study and analysis
Effectiveness of RCF
RCF의 효과를 보기 위해 Electricity와 Traffic에 대해 ablation 을 수행하였다.
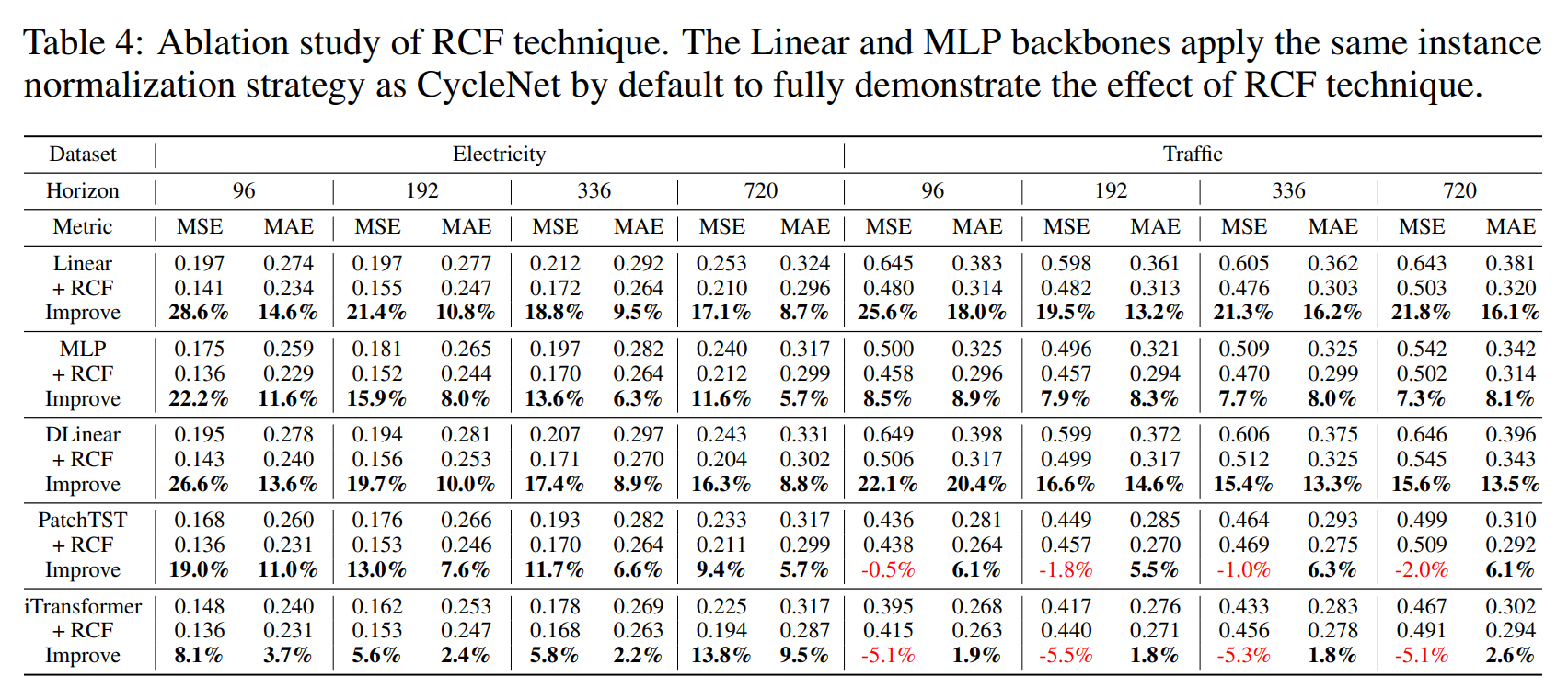
기본적인 Linear와 MLP에서 CycleNet을 추가하였을 때 아주 좋은 성능을 보였다. 또한 RCF를 다른 모델에 PatchTST, iTransformer 추가하였을 때에도 마찬가지로 20%에 가까운 성능 향상을 보였다.
그러나, PatchTST와 iTransformer 에 대해서 MSE가 낮아졌음에도 불구하고, 트래픽 데이터셋에서 RCF 성능이 떨어지게 된다. 이에 대한 추가적인 direction은 appendix 에서 다룬다.
Comparison of different STD techniques
LD from Leddam, MOV from DLinear, and Sparse technique from SparseTSF 와 비교한다. 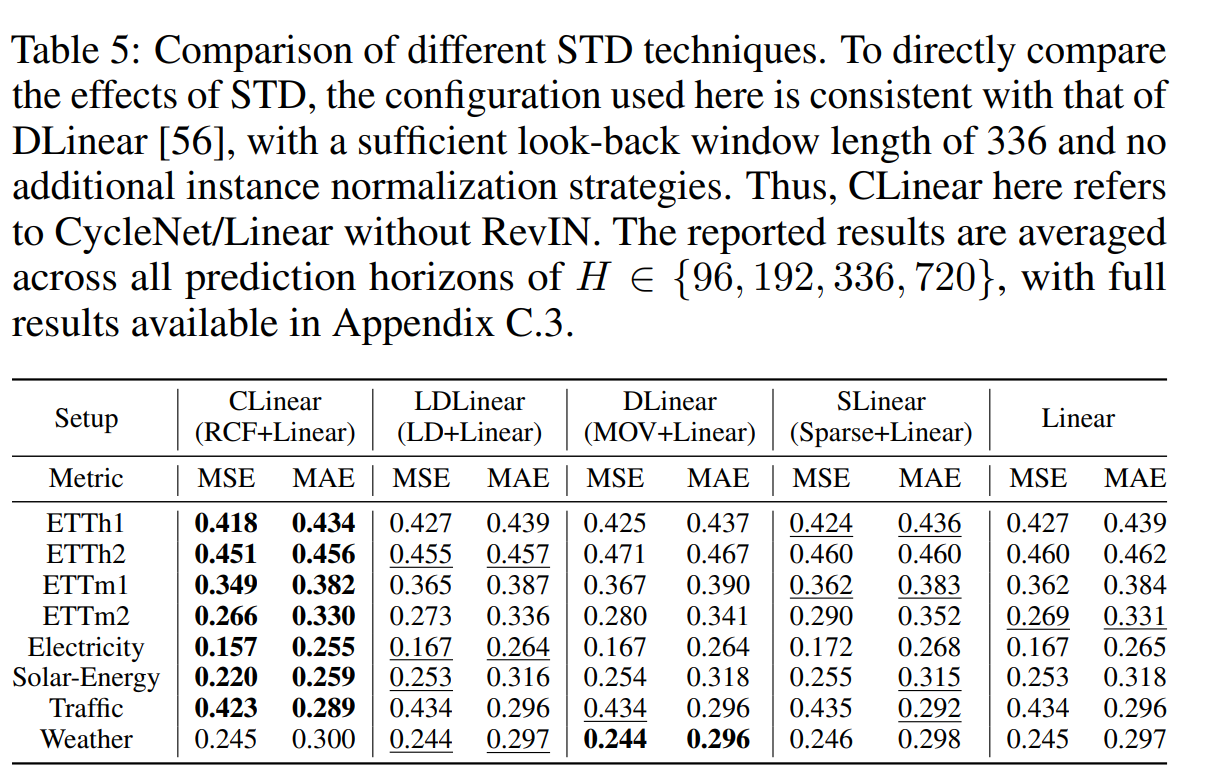
RCF는 다른 STD 방법론 대비 좋은 성능을 보인다. 특히 강한 주기성을 갖는 Electricity와 solar energy에서 특히 성능이 좋다. 이는 MOV와 LD 기반의 STD 방법론들은 trend 예측을 룩백 윈도우의 슬라이딩 aggregation을 통해서 수행하는데, 내제된 이슈가 있다. 슬라이딩 윈도우를 무빙 에버리지 취하는 방법을 하자면, 맥시멈 시즈널 컴포넌트의 주기보다 더 슬라이딩 윈도우의 길이가 커야 하낟. 그렇지 않으면, 분해를 하는 것이 불안정하게 된다.
또한, 제로 패딩을 항녀서 이동 평균 시퀀스를 얻게 되는데, 시퀀스 엣지 부분에서 패딩 부분의 왜곡이 일어난다. 게다가, 이러한 방법론들은 unbconstrained 혹은 weakly constrained linear regression라고 볼 수 있다.
반대로 전체의 학습이 수렴하였을때, 주기 컴포넌트들은 학습 셋에서 글로벌하게 예측이 된 것이고, 한정된 룩백 윈도우의 길이라는 한계점을 넘어 기존 리니어 리그레션의 한계를 넘을 수 있게 된 것이다.
Impact of hyperparameter
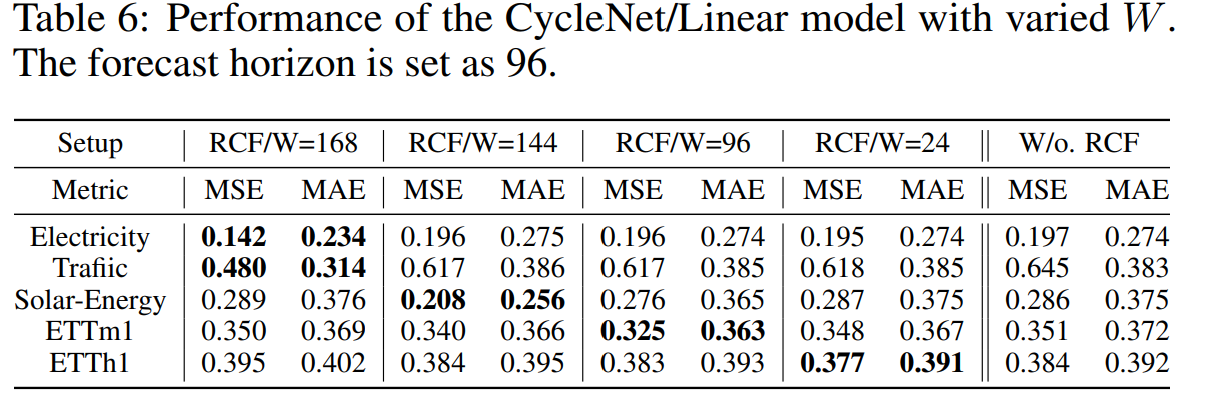
하이퍼파라미터 W를 통해서 RCF 테크닉에서 Q의 길이를 설정하게 된다. W를 데이테셋 전체 길이만큼 사용하게 되었을 때, RCF가 중요한 역할을 할 수 있다. 이는 정확한 W를 설정하는 것이 중요함을 알 수 있다. 게다가 W가 부정확하게 설정되었다면 모델의 퍼포먼스가 RCF가 사용되지 않은것과 유사함을 알 수 있다. 그러나 RCF의 worst 케이스를 고려하더라도 RCF가 사용되지 않은 것보다는 좋음을 알 수 있다.
Visualization of the learned periodic patterns
RCF 테크닉의 목적은 learnable recurrent cycles Q 를 모델하는 것이다. Fig 4. 는 다른 주기 패턴이 다른 데이터셋과 채널에서 얻어지는 것을 나타낸다.
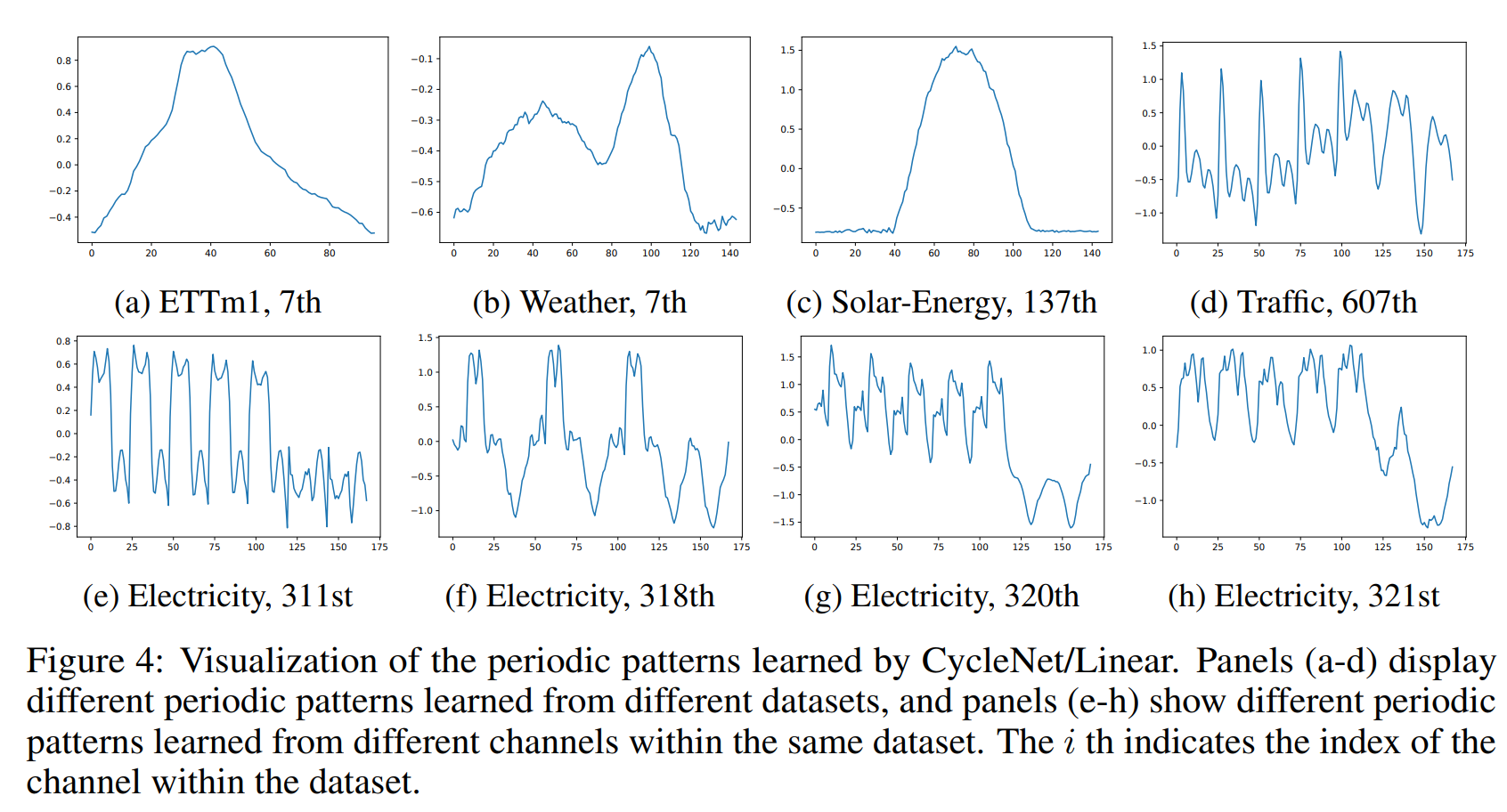
4(c)는 매일 반복되는 패턴을 의미하고, (d)는 주간으로 반복되는 트래픽 플로우를 나타낸다. 이러한 글로벌 시퀀스의 반복되는 패턴은 예측에서 보조 정보로써 사용되며, 룩백 윈도우 길이가 제한되는 상황, 그리고 주기가 매우 긴 상황에서 특히 잘 활용된다.
게다가, 다른 채널에 대해서 fig4.(e-h) 의 경우에는 채널마다 다른 패턴을 보인다. 4.f는 가구의 주간 전기 사용의 간헐적 패턴을 다루고, 나머지는 동일한 주간 패턴에 대해 다룬다. 이는 다양한 채널에 각기 다른 모델링을 독립적으로 수행해야 하는 이유를 설명해준다.
Performance with varied look-back length
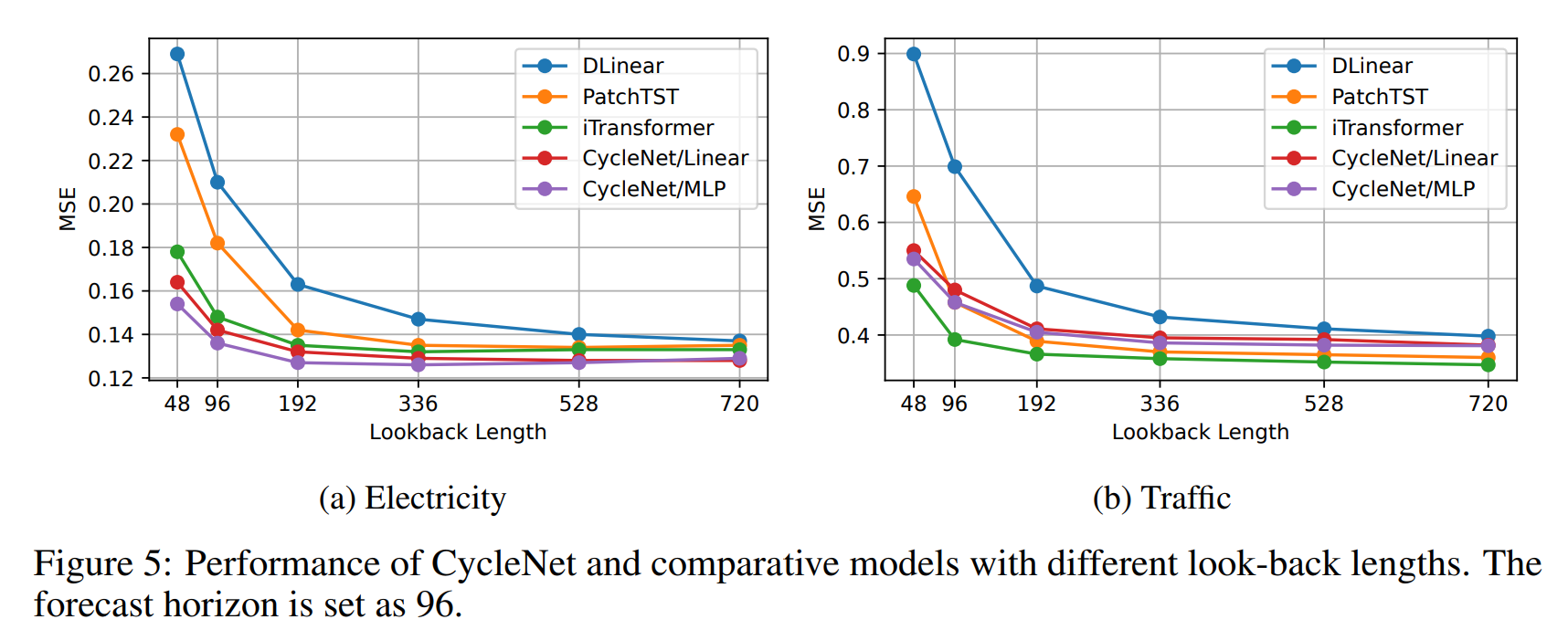
룩백 윈도우 길이에 따른 성능 비교를 수행하였다. Electricity에서는 SOTA 방법론대비 거의 모든 길이에서 성능이 좋음을 알 수 있다.
그러나 Traffic 에서는 아까 설명했다시피 iTransformer가 성능이 더 좋았다. 따라서 백본 모델에서 CycleNet을 활용할 때 이러한 변수간 공간-시간 관계가 중요한 데이터셋에 대해서는 다양한 시도가 필요하다.
5 Discussion
Potential limitations
Unstable cycle length
CycleNet은 EGG데이터와 같이 사이클 길이가 시가넹 따라 변화하는 데이터셋에서는 맞지 않다.
Varying cycle lengths across channels
다른 채널이 다른 주기 길이를 가진다면, CycleNet은 모든 채널을 같은 사이클 길이 W로 모델링을 하므로 맞지 않다. 이를 해결하기 위해서 전처리로 데이터 채널을 splitting을 하는 과정이 필요하다.
Impact of outliers
데이터셋이 아웃라이어를 포함하고 있다면, 퍼포먼스가 영향을 받을 수 있다. TCF의 작동 원리가 이전 데이터의 평균 사이클을 활용하기 때문이다. 따라서 이러한 아웃라이어가 존재하면 RCF가 학습하는 사이클 패턴이 달라지게 되며 부정확한 예측이 될 확률이 높다.
Long-range cycle modeling
일일 혹은 주간 사이클은 본 연구에서 잘 모델링 하였으나, 년도같은 긴 사이클의 모델링은 효과적이지 못했다. 이러한 케이스에 대해서는 추후 연구에서 발전시켜야 한다.
Future work: further modeling inter-channel relationships
RCF 테크닉은 모델의 시계열에 내재된 주기 패턴을 파악하고 활용하는데 사용된다. 변수간 시공간 관계를 가지는 시나리오에서는 SOTA 방법론에 비해 성능이 떨어지게 된다. 이를 수정하여 다변량 모델델링에서 채널간의 관계를 고려ㅛ하는 것은 가치가 있으므로, 미래 연구가 필요하다.
6 Conclusion
본 연구는 RCF 테크닉을 통해서 시계열의 내재된 주기 패턴을 파악하고 이를 직접적으로 모델링 함으로써 LSTF 태스크의 성능을 높였다. 제안 방법론은 심플한 MLP/Linear 모델에 적용되었을 때에도 SOTA 성능을 달성함을 보였다. 논 논문은 시계열 예측을 위해 주기성이 중요하며, 모델링 과정에 더 큰 비중을 두어야 한다는 것을 보였다. 또한 채널 간 관계 모델링을 하는 방법과 이를 CycleNet에 통합하는 과정이 가치 있는 미래 연구 방향임을 제시하였다.